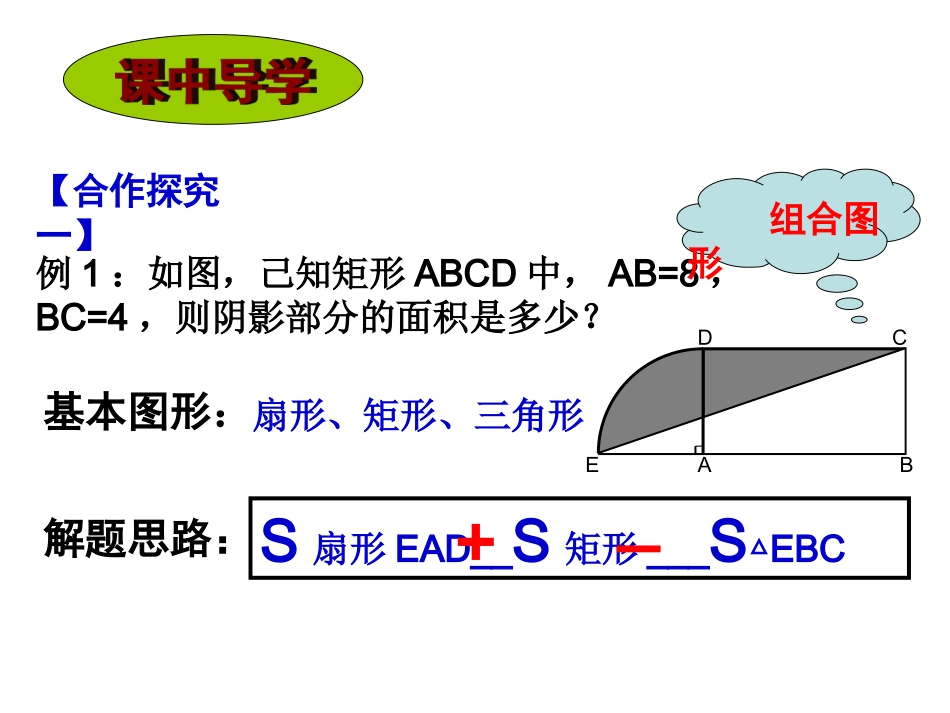
继续努力!相信自己!我们会做得更好!有关图形重叠部分面积的计算【学习目标】1、进一步理解掌握基本图形的面积公式,并能熟练计算。2、通过“转化”,会计算组合图形重叠部分(阴影部分)的面积。【学习准备】基本图形:ABCABCDOOAB【合作探究一】例1:如图,己知矩形ABCD中,AB=8,BC=4,则阴影部分的面积是多少?ABCDE基本图形:解题思路:扇形、矩形、三角形组合图形S扇形EAD__S矩形___SEBC△+_例2:如图,点A、B、C在直径为2的⊙O上,∠BAC=45°,则图中阴影部分的面积等于____。组合图形基本图形:扇形与三角形解题思路:S扇形BOC___SBOC△计算结果:214O结论1:利用_____来计算重叠部分的面积和差_【课中训练一】30°如图,在□ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是________。DAEBC33将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一条直线上.若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为cm2【合作探究二】例题:己知直经AB=10,点C、D是圆的三等分点,求阴影部分的面积。ABCDO组合图形解题思路:作辅助线,根据平行线之间距离相等,利用“同底等高”的三角形面积相等,转化为求扇形面积。计算结果:625根据平行线间的距离______,再利用__________的三角形面积相等进行转化求值。结论2:相等“同底等高”如图,A是半径为1的⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于。OABC【课中训练二】6【合作探究三】例题:如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP.若弦AB的长为6,则阴影部分的面积为_____9BACPO组合图形ABCOP解题思路:通过_____使两圆的圆心_____,即两圆为________。平移重合同心圆结论3:利用____来计算重叠部分的面积平移【课中训练三】如图,两圆内切,大半圆弦AB切小半圆于D,AB=6,则阴影部分的面积_____BO1OADBAOD29【合作探究四】例题:如图,三个圆是同心圆,则图中阴影部分的面积等于_______。组合图形4结论4:利用_____来求重叠部分的面积。旋转【课中训练四】如图,正方形的四个顶点在直径为4的大圆圆周上,四条边与小圆都相切,AB、CD过圆心O,且AB⊥CD,则图中阴影部分的面积是_______。ACBDO达标测评1、如图,扇形OAB中,∠AOB=60°AD=1,弧CD的长为,则图中阴影部分的面积为________。670CDAB60°2、在Rt△ABC中,∠C为直角,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为_________ABC425243、如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,OA=2,OC=1,试求阴影部分的面积。0BACD43(答案:)中考链接(2012山东省)如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是()(A)6π(B)5π(C)4π(D)3π*选做题:如图,在△ABC中,AB=AC=2.∠ABC=30°,以A为圆心,AB为半径作弧BEC,以BC为直径作半圆,求阴影部分的面积。CABEFA收获小结有关图形重叠部分(阴影部分)面积的计算方法1、利用和差来计算重叠部分的面积。2、利用“同底等高”的三角形面积相等进行转化求值。3、利用平移来计算重叠部分的面。4、利用旋转来求重叠部分的面积。