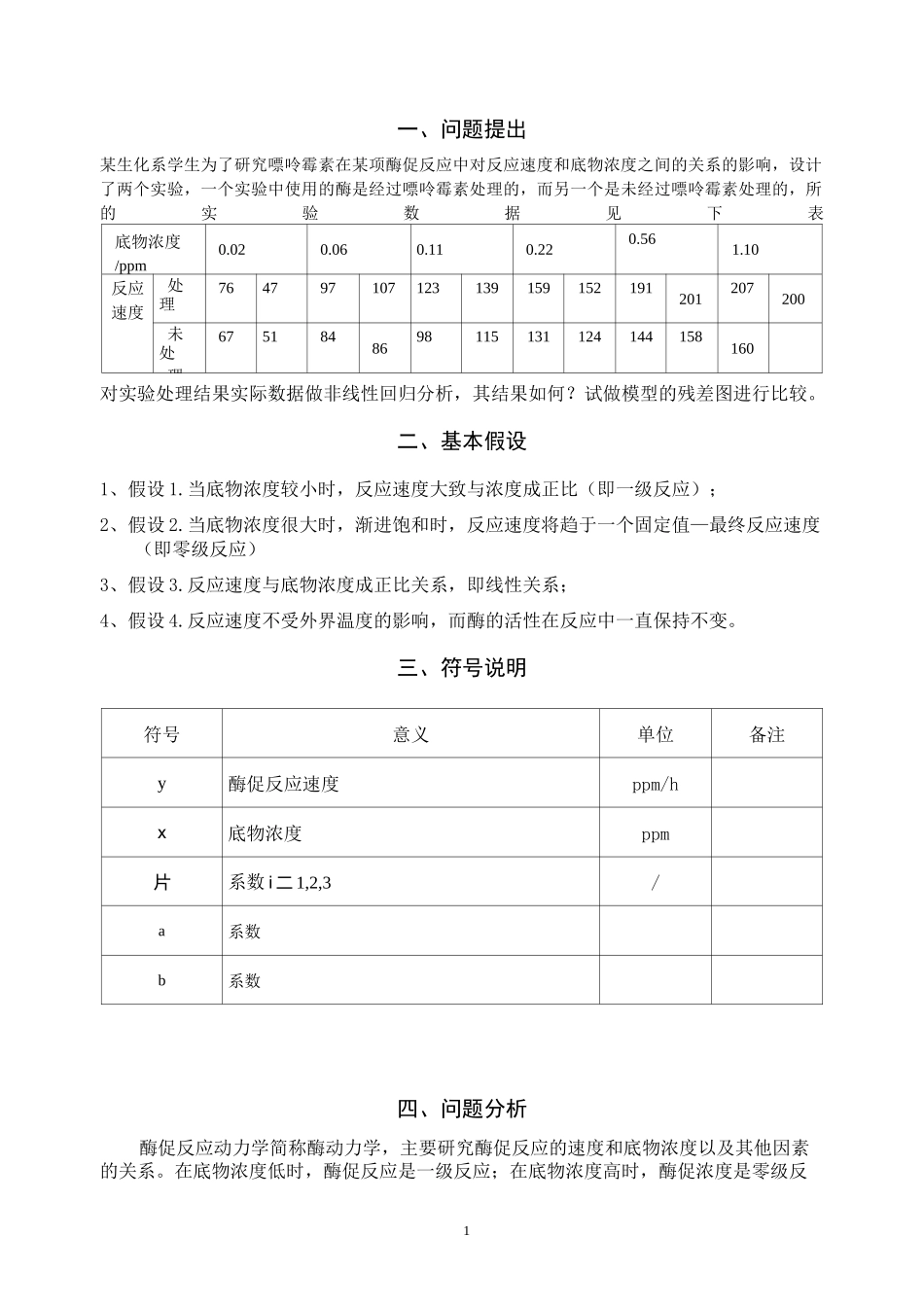
数学建模摘要本文针对嘌呤霉素在某项酶促反应中对反应速度和底物浓度之间的关系的影响的问题,根据实际可知符合底物浓度与反应速度的模型有两种,即Michaelis-Menten模型和指数增长模型。对于Michaelis-Menten模型,例题中已经详细分析,不再详细讨论。本论文旨在建立指数模型对实际数据进行拟合分析。由酶促反应的基本性质知,酶浓度x和反应速度y之间满足当底物浓度较小时,反应速度大致与浓度成正比;在底物浓度很大,渐进饱和时,反应速度将趋于一个固定值,由此建立一个指数增长模型y=f(x,卩)=P(1-e-P2x)并使用Matlab中nlinfit函数对给1出数据进行非线性回归,用cftool函数对结果进行验证,确定出P=192.09431P=11.3854此时R2=90.14%。2为使模型更加准确,改进模型为y=卩](e-P3X-e-^2X),用同样的方法进行拟合与分析,得出p=155.6149,P=17.8120和B=-0.2670,此时R2=94.11%。同过两1个对模型进行预2测与做残差图3等方法,我们发现第二个模型相比第一个有所改进。我们通过对实际问题的仔细分析,把实际问题转化成为数学上求解线性回归的问题,并建立了广为大家所熟悉的数学模型指数模型。通过数学软件的求解,得出模型中变量的系数。由于模型中的有些参数是估计的,考虑到实际与理论的差距,为了是使理论分析更贴近生活实际,我们从简略模型到优化模型进行了进一步分析,通过计算机利用数学软件MATLAB对问题进行了求解分析,得到了比较客观的分析结果。最后我们还根据模型的特点,对模型进行了推广,使其更具有一般性,能够解决更多实际问题。关键词:指数模型非线性回归MATLABnlinfitcftool残差图1一、问题提出某生化系学生为了研究嘌呤霉素在某项酶促反应中对反应速度和底物浓度之间的关系的影响,设计了两个实验,一个实验中使用的酶是经过嘌呤霉素处理的,而另一个是未经过嘌呤霉素处理的,所的实验数据见下表底物浓度/ppm0.020.060.110.220.561.10反应速度处理764797107123139159152191201207200未处理6751848698115131124144158160对实验处理结果实际数据做非线性回归分析,其结果如何?试做模型的残差图进行比较。二、基本假设1、假设1.当底物浓度较小时,反应速度大致与浓度成正比(即一级反应);2、假设2.当底物浓度很大时,渐进饱和时,反应速度将趋于一个固定值—最终反应速度(即零级反应)3、假设3.反应速度与底物浓度成正比关系,即线性关系;4、假设4.反应速度不受外界温度的影响,而酶的活性在反应中一直保持不变。三、符号说明符号意义单位备注y酶促反应速度ppm/hx底物浓度ppm片系数i二1,2,3/a系数b系数四、问题分析酶促反应动力学简称酶动力学,主要研究酶促反应的速度和底物浓度以及其他因素的关系。在底物浓度低时,酶促反应是一级反应;在底物浓度高时,酶促浓度是零级反2应。y=卩](e-卩3x一e-卩2x)当反应浓度低时,反应速度大致与浓度成正比;当浓度很大时,渐进饱和时,反应速度趋近于一个固定值一一最终反应速度。以下指数增长模型满足这个性质即y=f(x,卩)=卩(1-e-P2x)与1下面分别对这两个模型进行分析求解。五、模型的建立与求解5.1模型一建立与求解5.1.1模型一的分析由给出模型,先用Matlab中的nlinfit函数可求出系数,此处需先给出系数的初始值进行迭代,根据函数意义,P为最终反映速度,反映该酶促反应达最终速度的快慢,粗略估其值为220与10.125.1.2模型一模型的建立y二卩(1-e-卩2x)15.1.3模型一模型的求解利用MATLAB统计工具箱中的nlinfit命令代入初值进行求解,将得到的结果作为初值再次代入到模型中求解,得到稳定的系数(见下表)。参数参数估计值参数置信区间P1192.0945[173.8772210.3117]P211.3854[7.757115.0137]rmse(剩余标准差)=17.440035.1.4模型一结果的分析及验证用MATLAB中eftool函数进行验证,得出结果如下:f(x)=a*(1-exp((-b)*x))Coeffieients(with95%eonfideneebounds):a=192.1(173.9,210.3)b=11.38(7.757,15.01)Goodnessoffit:SSE(残差平方和):3042R-square:0.9014AdjustedR-square:0.8916RMSE:17.44有上述两种模型可以得出P1、卩2的参数估计值,以及置信区间。5.2模型二模型建立与求解5.2.1模型二的分析因反映中...