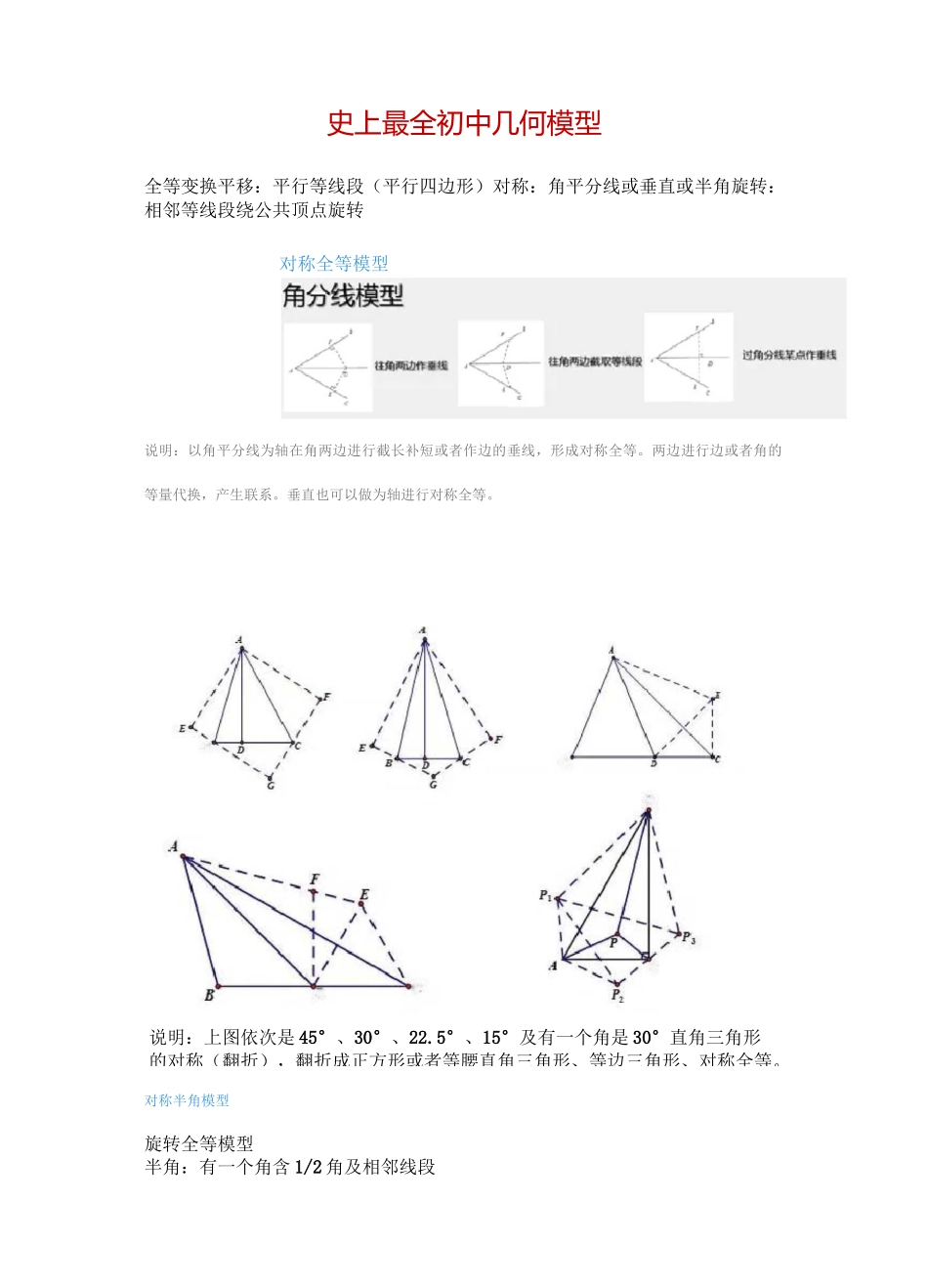
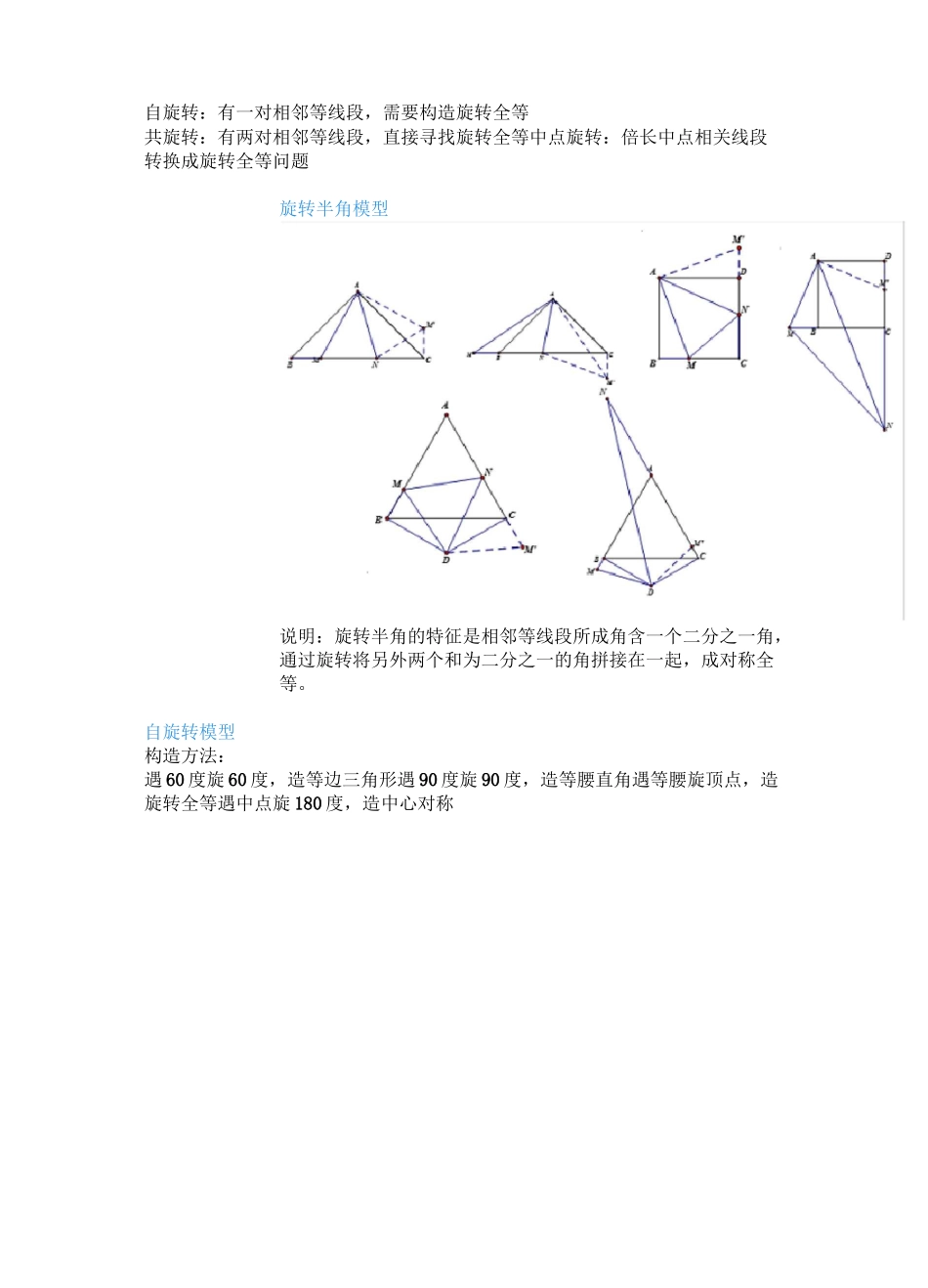
EE号ccD说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。史上最全初中几何模型全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。对称半角模型旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容通。过“8”字模型可以证明。模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。说明:两个正方形、两个中点模型it中审伦沪边就中位密怖逼三議4御蒂貝边中歿几何最值模型对称最值(两点间线段最当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。中点旋转:m:a4加小模型R«l>翼段之和轴对称模型三践段之利廉短棋型过侨悅唱同侧.异側两线段之堆址小松舉三痢场周出巔小模型线段和差模型411WM说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。旋转最值(共线有最值)说明:找到与所要求最值相关成三角形的两个定长线段定长线段的和为最大值,定长线段的差为最小值。正方形+等腰直角三角形-正方形剪拼模型三角形9四边形说明:剪拼主要是通过中点的180度旋转及平移改变图形的形状。说明:通过射影定理找到正方形的边长,通过平移与旋转完成形状改变矩形-正方形匚EE说明:两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似。健转相徵模面积等推广:两个任意相似三角形旋转成一定角度,成旋转相似。第三边所成夹角符合旋转“8”字的规律。说明:注意边和角的匹应「相等绘段或者相番比值在证明相似中起到通过等量代按来构造相忙西形的作月.说明:⑴三垂直到」钱三等庠的演变,三等角以30滾、45良60复形式出现的居多。(2)内外角平分线走理到射彩走理的游变•注息之间的柏同与不同之处。另外,怡似、射彫走理、杞交弦走理(可以准广到匝1鬲走理)N间的比值可以转涣成乗枳.通过等岌段、等比值、等乘积送行代涣.进行证明得到需要的结论。说明:相似证明中最耸用的铺助线是做平行.根据題目的条件或者结论的比值来傲相应的平行^A模型一二手拉手模型-族转型全等(2)«*7A>条件:5勺笳初直角三角形a结论:①儿②—£方・90°,>③OE平分一ED.<»>任斌尊1»三角形a条件:乩"疋。均为苓腫三角形a结论:①AOXC?■NOBD.②/LAEB■LAOB;»②OF平分/>nA杀件:从皿皿。劝弄边三角刑a结论:①AO4C・MMD$②£J£fi-60°;③OE平分LAED.A模型二手拉手模型-旋转型相似>CD//AB9将AOCQ検转至右图位賈A结论:a右图中①AOC2AOAB8AOACM)BD}a②运长局交加于点卫必有厶BEC・乙BCU<2>删曲况>糸件:CDHAB9LAOB・90°,将"疋》踏专至右囹位!S>偌论:右图中0)AOCgAO*〃QAO/ICM)BD)②延*/C交BD干点E,込有厶BEC•LBOA,lanZfXDj④BD丄彳C;©ii接a.BC,AD:*BC■AB'*CDy⑥S“““-訐CxBD(对角纟垣*睡直的四酬)A模型三:对角互补模型⑴全等型刖a条件:①厶OB・ZJX?£・90°丿②g平分"(出a结论,®CD=C£②OD^OE■J1OC丿③S(HKt•S皿♦SMt-^OC2ainw^:①作垂言.如圉F避月"'DM•ZEN,②过点C作佯丄OC.如上图(右),证明AODC・MEC\>当的一边交加的延於好点D时舟以±£偉论:(DCD-CE《不变)j©OE-OD->/20C,@"曲■仏“-2