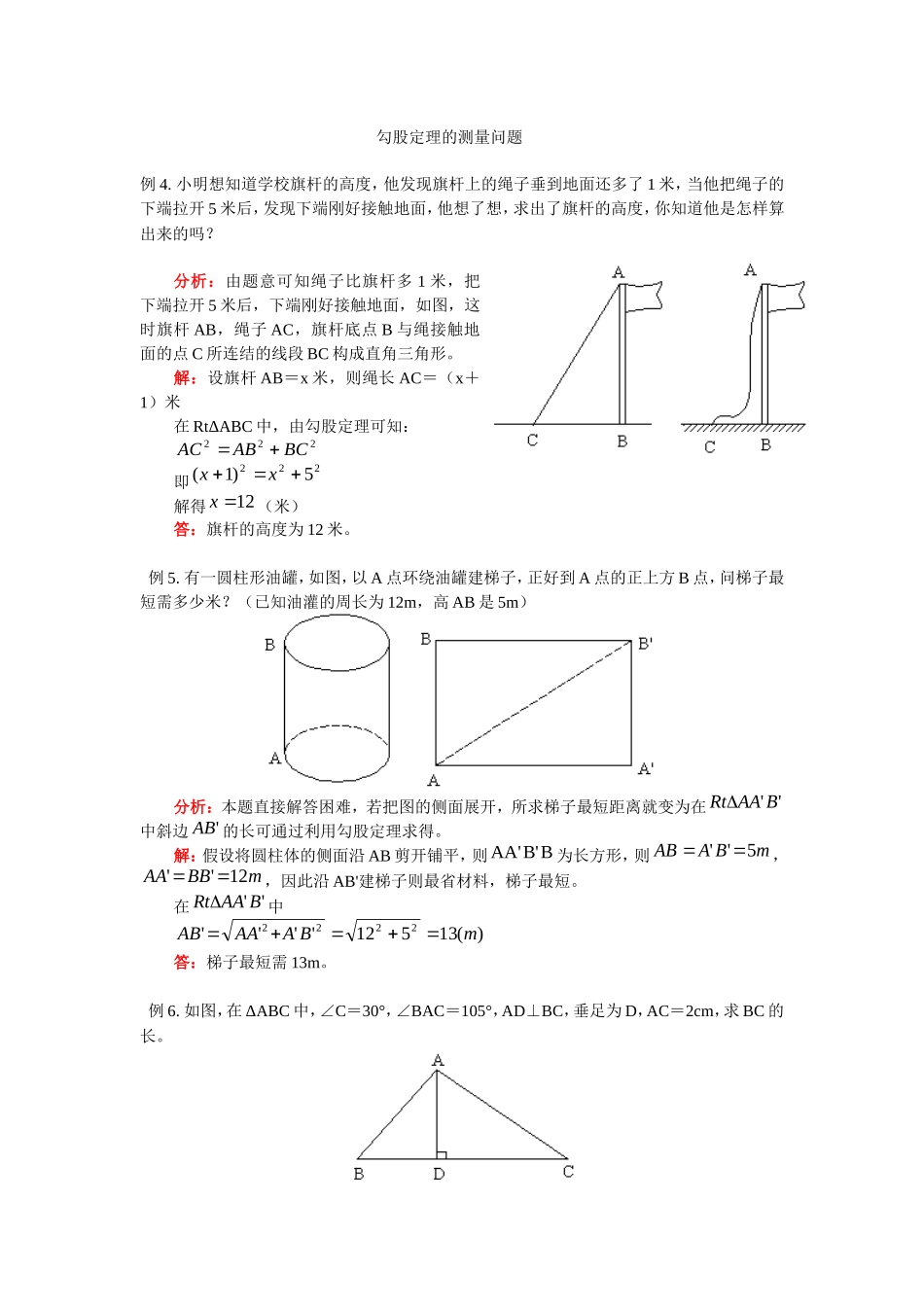
勾股定理的测量问题例4.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多了1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,他想了想,求出了旗杆的高度,你知道他是怎样算出来的吗?分析:由题意可知绳子比旗杆多1米,把下端拉开5米后,下端刚好接触地面,如图,这时旗杆AB,绳子AC,旗杆底点B与绳接触地面的点C所连结的线段BC构成直角三角形。解:设旗杆AB=x米,则绳长AC=(x+1)米在RtΔABC中,由勾股定理可知:222BCABAC即2225)1(xx解得12x(米)答:旗杆的高度为12米。例5.有一圆柱形油罐,如图,以A点环绕油罐建梯子,正好到A点的正上方B点,问梯子最短需多少米?(已知油灌的周长为12m,高AB是5m)分析:本题直接解答困难,若把图的侧面展开,所求梯子最短距离就变为在''BAARt中斜边'AB的长可通过利用勾股定理求得。解:假设将圆柱体的侧面沿AB剪开铺平,则B'B'AA为长方形,则mBAAB5'',mBBAA12'',因此沿AB'建梯子则最省材料,梯子最短。在''BAARt中)(13512''''2222mBAAAAB答:梯子最短需13m。例6.如图,在ΔABC中,∠C=30°,∠BAC=105°,AD⊥BC,垂足为D,AC=2cm,求BC的长。解析: 在ΔABC中,AD⊥BC∴ΔADC为RtΔ ∠C=30°ACAD21 AC=2∴AD=14560105DACBACBAD60DAC105BAC312ADACDC2222,即RtΔABD为等腰三角形∴BD=AD=1∴BC=DB+DC=(1+3)(cm)例7.如图,已知BC=9,AB=17,AC=10,AD⊥BC于D,求AD的长。分析:无论把AD放在直角ΔADC还是在直角ΔADB中,都不易直接利用勾股定理计算AD,必须先求出CD的长才能解决问题,需求CD的长,可设CD=x,设法找到关于x的方程,通过解方程的方法求出未知的CD长,题中的AD可作为解题的桥梁,列出方程。解:设CD=x,在直角三角形ADC中2222210xCDACAD在直角ΔABD中222222222)9(1710)9(17xxxBDABAD解得6x例8.如图分别以直角三角形的三边为边长向外作正三角形,试探索三个正三角形面积间的关系。分析:首先应探索出正三角形的面积与正三角形的边长之间的关系,然后可设出直角ΔABC的各边长,分别计算SI、SII、SIII,再进行比较。一、填空题861022AD1.在RtΔABC中,∠C=90°,若AC=5,AB=13,则BC=________。2.在直角三角形中有两边的长为3和4,则第三边的长为________。3.如图1,在直角梯形ABCD中,已知底AD=6cm,BC=11cm,腰CD=12cm,则直角梯形的周长为________。图14.直角三角形的周长为62,斜边的长为2,则此三角形面积为________。5.若222543,则将等式两边乘以3得27、48、75为边的三角形________(①不是直角三角形,②是直角三角形)6.一个等腰三角形周长是16cm,底边上的高是4cm,则三角形各边长为________。7.若一个直角三角形的三边为三个连续的偶数,则它的周长为________。8.如果一个直角三角形的三边为三个连续的整数,则它的面积为________。9.若直角三角形的两条直角边各扩大一倍,则斜边扩大________倍。10.正方形的面积为236cm,是其对角线长为________cm。二、选择题1.等腰直角三角形斜边为10,则其直角边为()A.25B.34C.52D.322.矩形的周长为20m,宽为2m,则对角线长为()A.m35B.m112C.m172D.m1323.ΔABC中,若∠A:∠B:∠C=1:2:3,则BC:AC:AB的值为()A.3:2:1B.3:2:1C.2:1:3D.2:3:14.直角三角形两直角边的长分别为5,12,则斜边上的高为()A.6B.8C.1380D.13605.已知在ΔABC中,a=3,633cb,,则∠A,∠B分别为()A.60°,30°B.30°,60°C.70°,60°D.60°,90°6.在RtΔABC中,∠C=90°,已知104:3:cba,,则ΔABC面积为()A.24B.12C.28D.307.三角形三边的长分别为a、b、c,且0)()(22222cbaba,则三角形的形状为()A.任意等腰三角形B.任意直角三角形C.等腰直角三角形D.等边三角形8.一直角三角形的斜边长比直角边大2,另一直角边为6,则斜边长为()A.4B.8C.10D.129.已知一个直角三角形的周长为30cm,面积为30cm2,那么这个直角三角形的斜边长为()A.15B.14C.13D.1210.ΔABC的三边长分...