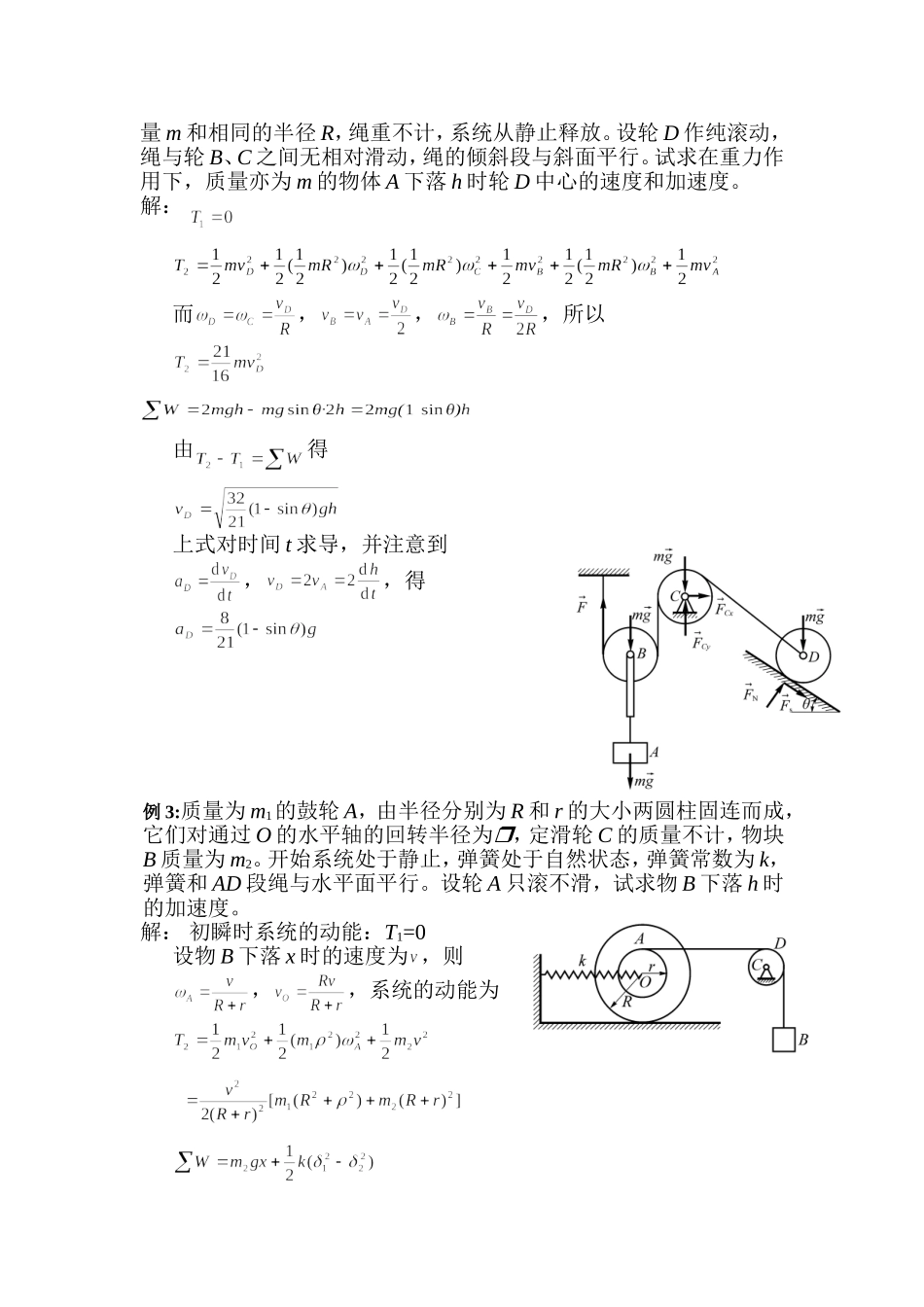
例1:在图示机构中,已知:匀质轮C作纯滚动,半径为r,质量为m3,鼓轮B的内径为r,外径为R,对其中心轴的回转半径为ρ,质量为m2,物A的质量为m1。绳的CE段与水平面平行,系统从静止开始运动。试求:(1)物块A下落距离s时轮C中心的速度与加速度;(2)绳子AD段的张力。解:研究系统:T2-T1=ΣWi+JCω2+JBω2+=m1gs式中:,代入得:vC=式两边对t求导得:aC=对物A:m=Σ,即:m1aA=m1g-FADFAD=m1g-m1aA=m1g-例2:三个均质轮B、C、D,具有相同的质量m和相同的半径R,绳重不计,系统从静止释放。设轮D作纯滚动,绳与轮B、C之间无相对滑动,绳的倾斜段与斜面平行。试求在重力作用下,质量亦为m的物体A下落h时轮D中心的速度和加速度。解:而,,,所以由得上式对时间t求导,并注意到,,得例3:质量为m1的鼓轮A,由半径分别为R和r的大小两圆柱固连而成,它们对通过O的水平轴的回转半径为,定滑轮C的质量不计,物块B质量为m2。开始系统处于静止,弹簧处于自然状态,弹簧常数为k,弹簧和AD段绳与水平面平行。设轮A只滚不滑,试求物B下落h时的加速度。解:初瞬时系统的动能:T1=0设物B下落x时的速度为,则,,系统的动能为其中,由,并对时间t求导,得当x=h时,例4:在图示系统中,物块A、B的质量分别为mA、mB,它们与接触面间的动摩擦系数都是f;均质滑轮的半径为R,质量为m。若绳与滑轮间无相对滑动,它的两段分别与水平面和斜面平行,试求物块A沿斜面下滑的加速度。解:其中,,,于是由有条件:若,则无滑动。例5:在图示机构中,鼓轮O重为G,内外半径分别为r和R,R=2r,对转轴的回转半径。物体A重P1,物体B重P2,且,B物与倾角为的斜面的动摩擦系数为f,绳的倾斜段与斜面平行,开始时系统静止。试求当物体A下降任意高度h时,鼓轮的角速度和角加速度。解:其中,其中,由有(1)式(1)对时间t求导得例6:在图示机构中,已知:匀质鼓轮O的质量为m1,外半径为R,内半径为r,对O的回转半径为ρ,其上绕有细绳,一端吊一质量为m2的物块A,另一端与匀质轮C相连,轮作纯滚动,质量为m3,半径为r,斜面倾角φ=30˚,绳的倾斜段与斜面平行。试求:(1)鼓轮的角加速度;(2)斜面的摩擦力及连接物块A的绳子的张力(表示成角加速度的函数)。例7:在图示机构中,已知:匀质圆盘A的质量为m1,匀质轮O的质量为m2,半径均为R,斜面的倾角为β,圆盘A沿斜面作纯滚动,轮O上作用一力偶矩为M的常值力偶。试求:(1)轮O的角加速度;(2)绳的拉力F(表示成角加速度的函数);(3)圆盘与斜面间的摩擦力Fs(表示成角加速度的函数)。