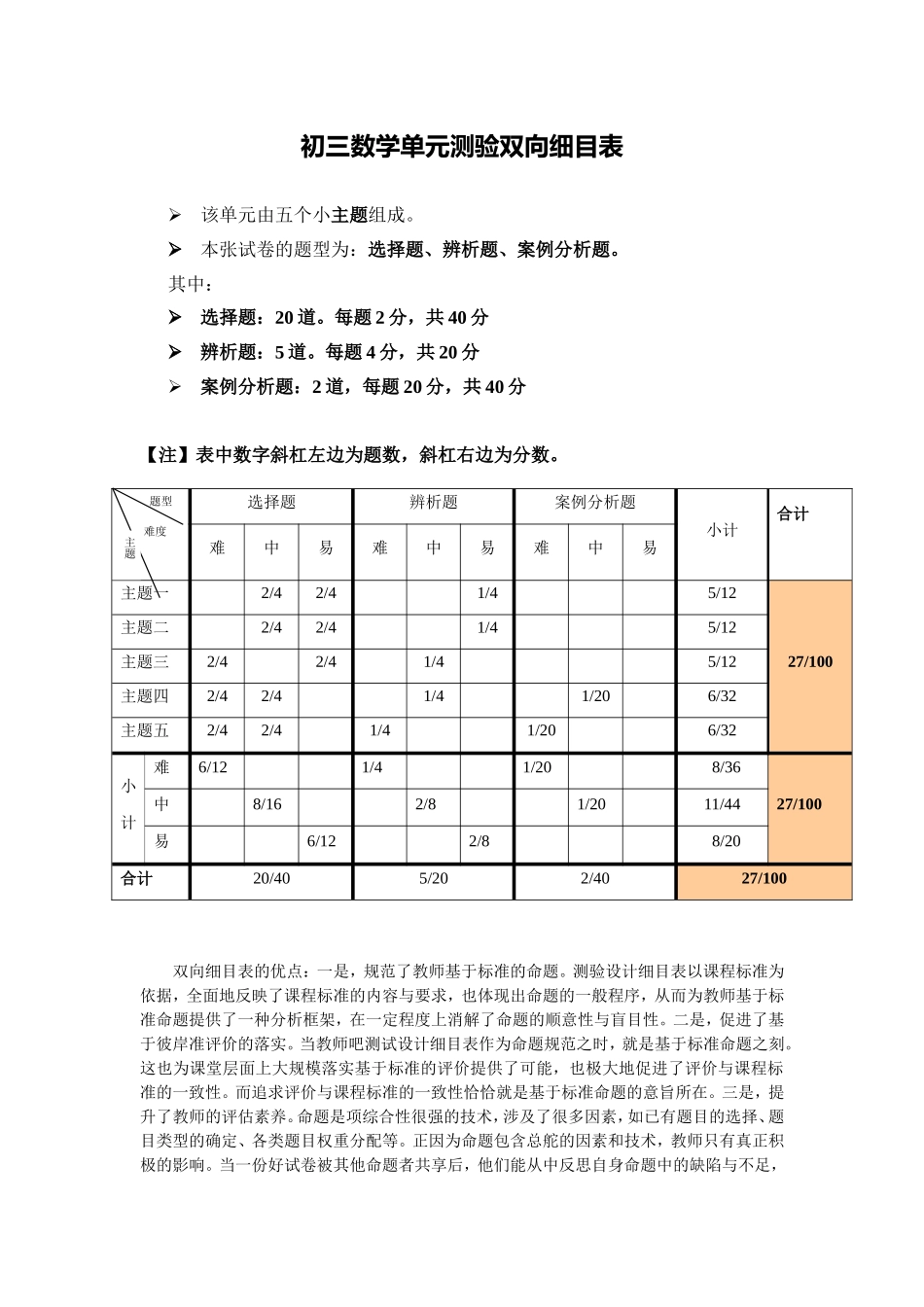
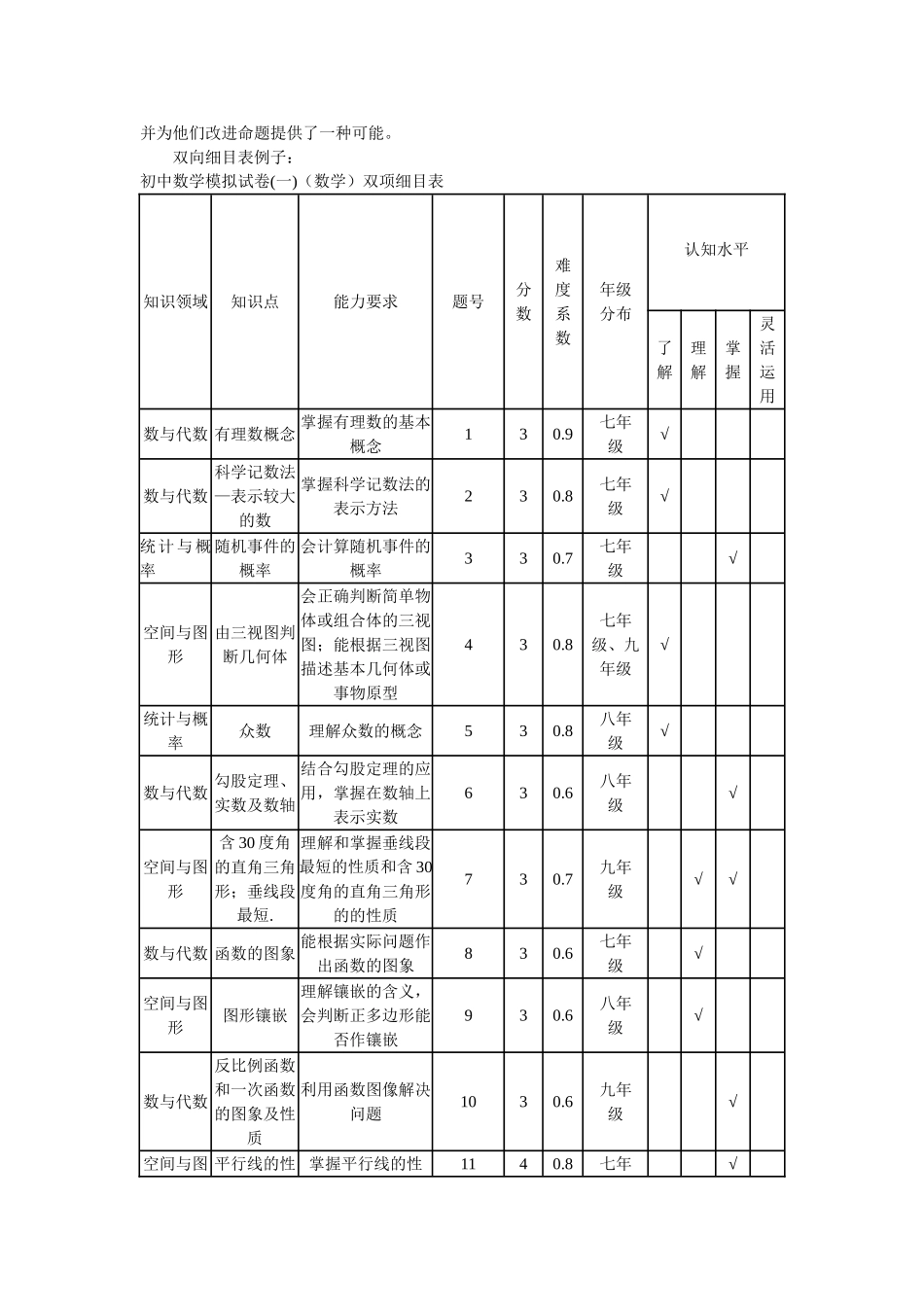
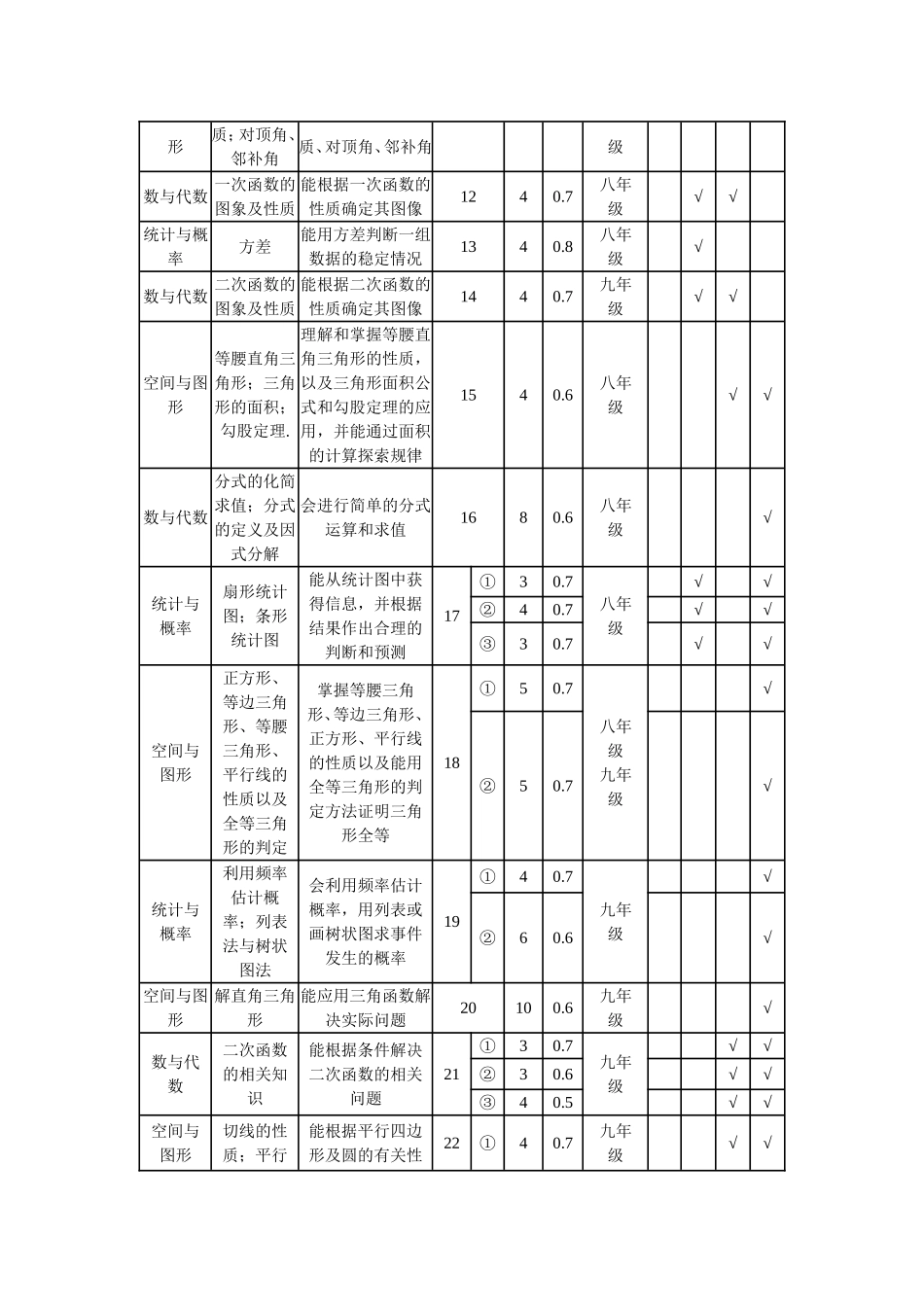
初三数学单元测验双向细目表该单元由五个小主题组成。本张试卷的题型为:选择题、辨析题、案例分析题。其中:选择题:20道。每题2分,共40分辨析题:5道。每题4分,共20分案例分析题:2道,每题20分,共40分【注】表中数字斜杠左边为题数,斜杠右边为分数。题型难度选择题辨析题案例分析题小计合计难中易难中易难中易主题一2/42/41/45/1227/100主题二2/42/41/45/12主题三2/42/41/45/12主题四2/42/41/41/206/32主题五2/42/41/41/206/32小计难6/121/41/208/3627/100中8/162/81/2011/44易6/122/88/20合计20/405/202/4027/100双向细目表的优点:一是,规范了教师基于标准的命题。测验设计细目表以课程标准为依据,全面地反映了课程标准的内容与要求,也体现出命题的一般程序,从而为教师基于标准命题提供了一种分析框架,在一定程度上消解了命题的顺意性与盲目性。二是,促进了基于彼岸准评价的落实。当教师吧测试设计细目表作为命题规范之时,就是基于标准命题之刻。这也为课堂层面上大规模落实基于标准的评价提供了可能,也极大地促进了评价与课程标准的一致性。而追求评价与课程标准的一致性恰恰就是基于标准命题的意旨所在。三是,提升了教师的评估素养。命题是项综合性很强的技术,涉及了很多因素,如已有题目的选择、题目类型的确定、各类题目权重分配等。正因为命题包含总舵的因素和技术,教师只有真正积极的影响。当一份好试卷被其他命题者共享后,他们能从中反思自身命题中的缺陷与不足,主题并为他们改进命题提供了一种可能。双向细目表例子:初中数学模拟试卷(一)(数学)双项细目表知识领域知识点能力要求题号分数难度系数年级分布认知水平了解理解掌握灵活运用数与代数有理数概念掌握有理数的基本概念130.9七年级√数与代数科学记数法—表示较大的数掌握科学记数法的表示方法230.8七年级√统计与概率随机事件的概率会计算随机事件的概率330.7七年级√空间与图形由三视图判断几何体会正确判断简单物体或组合体的三视图;能根据三视图描述基本几何体或事物原型430.8七年级、九年级√统计与概率众数理解众数的概念530.8八年级√数与代数勾股定理、实数及数轴结合勾股定理的应用,掌握在数轴上表示实数630.6八年级√空间与图形含30度角的直角三角形;垂线段最短.理解和掌握垂线段最短的性质和含30度角的直角三角形的的性质730.7九年级√√数与代数函数的图象能根据实际问题作出函数的图象830.6七年级√空间与图形图形镶嵌理解镶嵌的含义,会判断正多边形能否作镶嵌930.6八年级√数与代数反比例函数和一次函数的图象及性质利用函数图像解决问题1030.6九年级√空间与图平行线的性掌握平行线的性1140.8七年√形质;对顶角、邻补角质、对顶角、邻补角级数与代数一次函数的图象及性质能根据一次函数的性质确定其图像1240.7八年级√√统计与概率方差能用方差判断一组数据的稳定情况1340.8八年级√数与代数二次函数的图象及性质能根据二次函数的性质确定其图像1440.7九年级√√空间与图形等腰直角三角形;三角形的面积;勾股定理.理解和掌握等腰直角三角形的性质,以及三角形面积公式和勾股定理的应用,并能通过面积的计算探索规律1540.6八年级√√数与代数分式的化简求值;分式的定义及因式分解会进行简单的分式运算和求值1680.6八年级√统计与概率扇形统计图;条形统计图能从统计图中获得信息,并根据结果作出合理的判断和预测17①30.7八年级√√②40.7√√③30.7√√空间与图形正方形、等边三角形、等腰三角形、平行线的性质以及全等三角形的判定掌握等腰三角形、等边三角形、正方形、平行线的性质以及能用全等三角形的判定方法证明三角形全等18①50.7八年级九年级√②50.7√统计与概率利用频率估计概率;列表法与树状图法会利用频率估计概率,用列表或画树状图求事件发生的概率19①40.7九年级√②60.6√空间与图形解直角三角形能应用三角函数解决实际问题20100.6九年级√数与代数二次函数的相关知识能根据条件解决二次函数的相关问题21①30.7九年级√√②30.6√√③40.5√√空间与图形切线的性质;平行能根据平行四边形及圆的有关性22①40.7九年级√√四边形的性质;扇...