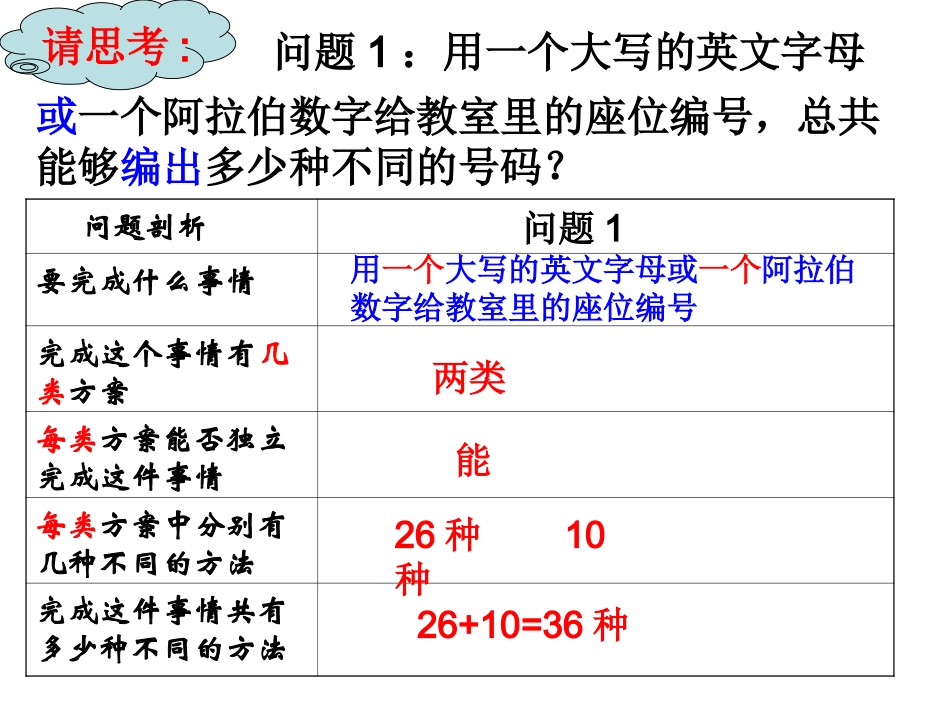
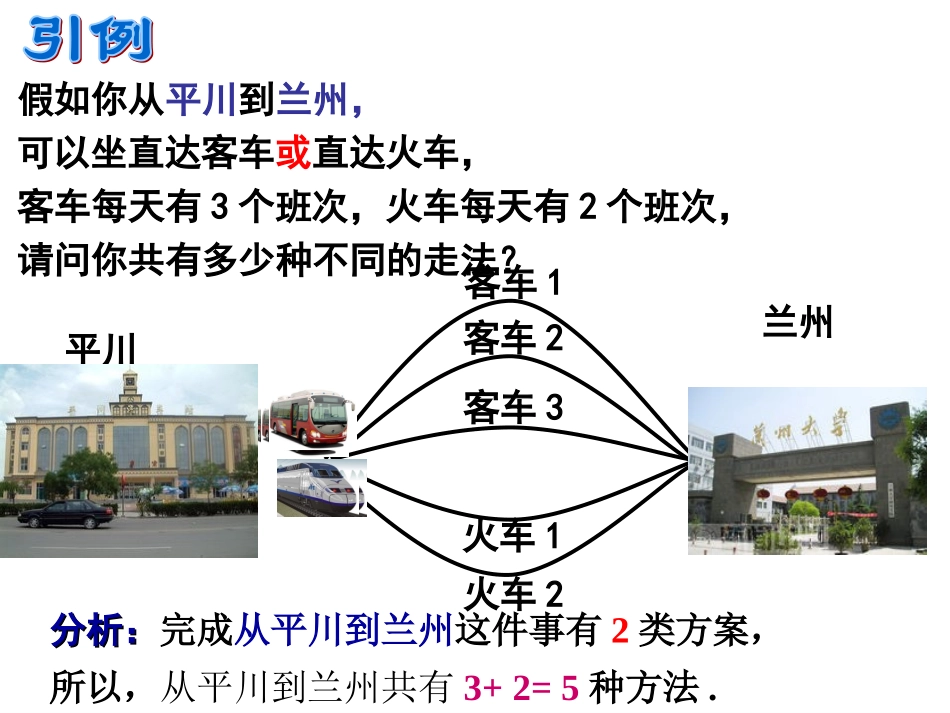
1.1分类计数原理与分步计数原理问题剖析问题1要完成什么事情完成这个事情有几类方案每类方案能否独立完成这件事情每类方案中分别有几种不同的方法完成这件事情共有多少种不同的方法两类能26种10种26+10=36种或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?请思考:问题1:用一个大写的英文字母用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号假如你从平川到兰州,请问你共有多少种不同的走法?客车每天有3个班次,火车每天有2个班次,可以坐直达客车或直达火车,客车1客车2客车3火车1火车2平川兰州分析:分析:完成从平川到兰州这件事有2类方案,所以,从平川到兰州共有3+2=5种方法.问题1:你能否发现这两个问题有什么共同特征?1、都是要完成一件事2、用任何一类方法都能直接完成这件事3、都是采用加法运算你能总结出这类问题的一般解决规律吗?你能总结出这类问题的一般解决规律吗?完成一件事有两类不同的方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法。例1.在填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:A大学B大学生物学化学医学物理学工程学数学会计学信息技术学法学如果这名同学只能选一个专业,那么他共有多少种选择呢?变式:在填写高考志愿表时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,具体情况如下:A大学B大学生物学化学医学物理学工程学数学会计学信息技术学法学如果这名同学只能选一个专业,那么他共有多少种选择呢?C大学机械制造建筑学广告学汉语言文学韩语N=5+4+5=14(种)如果完成一件事情有3类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3类方案中有m3种不同的方法,那么完成这件事情有种不同的方法N=m1+m2+m3探究1如果完成一件事情有n类不同方案,在每一类中都有若干种不同方法,那么应当如何计数呢?完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,那么完成这件事共有种不同的方法。……在第n类方案中有mn种不同的方法,nmmmN21引例1:用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?变换:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?分析:分析:完成给教室里的座位编号编号这件事分两步完成:第1步:先确定一个英文字母第2步,后确定一个阿拉伯数字字母数字得到的号码123456789A1A2A3A4A5A6A7A8A9树形图树形图ABB1B2B3B4B5B6B7B8B9CC1C2C3C4C5C6C7C8C9DD1D2D3D4D5D6D7D8D9EE1E2E3E4E5E6E7E8E9FF1F2F3F4F5F6F7F8F9变换:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?分析:分析:完成给教室里的座位编号这件事需要两个步骤,第1步,确定一个英文字母,有6种不同方法;第2步,确定一个阿拉伯数字,有9种不同方法;所以,编号共有6×9=54种方法.例2、设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?例3、北京的部分电话号码是0943665××××,后面每个数字来自0~9这10个数,问可以产生多少个不同的电话号码?变式:若要求最后4个数字不重复,则又有多少种不同的电话号码?094366510101010×××=104分析:分析:=504010987×××完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有种不同的方法.N=m+n分类加法计数原理:完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法.那么完成这件事共有N=m×n分步乘法计数原理:种不同的方法.那么完成这件事共有种不同的方法。nmmmN21完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……做第n步有mn种不同的方法,两个计数原理两个计数原理分类加法计数原理分步乘法计数...