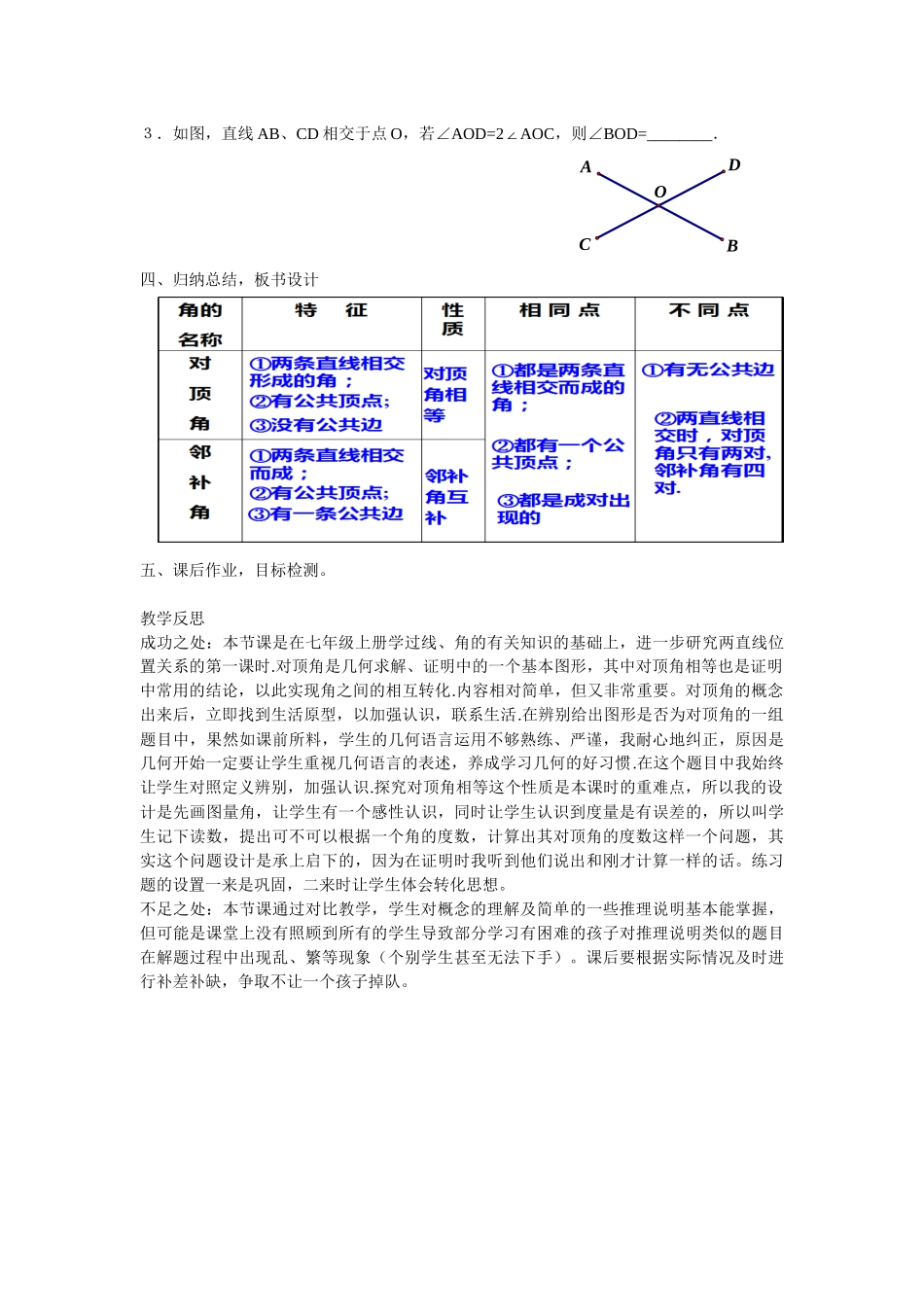
第1课时相交线教学内容5.1.1相交线教学目标1.理解对顶角和邻补角的概念,能在图形中辨认.2.掌握对顶角相等的性质和它的推证过程.3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.教学重点:在较复杂的图形中准确辨认对顶角和邻补角.教学难点:在较复杂的图形中准确辨认对顶角和邻补角.一、创设情境,引入课题问题:请同学们观察下面的图片,说一说那些道路是交错的,那些是平行的?教师导入:图中的道路是有宽度的,是有限长的,而且也不是完全直的,当我们把它们看成直线时,这些直线有些是相交线,有些是平行线.相交线、平行线都有许多重要性质,并且在生产和生活中有广泛应用.所以研究这些问题对今后的工作和学习都是有用的,也将为后面的学习做些准备.我们先研究直线相交的问题.二、目标导学,探索新知目标导学一:理解对顶角和邻补角的概念,并会在图形中进行辨别1.观察图片,注意剪刀剪开布片过程中有关角的变化.2.将剪刀抽象为几何图形并画一画.答:如图2几何语言描述图形:直线AB、CD相交于点O.概念:如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。3.观察上图,同桌讨论。(1)两条直线相交组成几个角?(2)这两条直线相交得到哪几对角?(3)每对角中两个角的位置有怎样的关系?(4)根据它们的位置和度数的关系将这几对角进行分类.4.概念归纳(1)∠1与∠3是直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角.(2)∠1与∠2是直线AB、CD相交得到的,有公共顶点O,且有一条公共边,像这样的两个角叫做邻补角.5.概念深化(1)找一找上图中还有没有对顶角,如果有,是哪两个角?(2)找一找上图中还有没有邻补角,如果有,是哪两个角?学生口答:∠2和∠4再也是对顶角.∠3与∠2、∠1与∠4、∠3与∠4也互为邻补角。4231图2DCBA6.初步应用例1:(1)下列图中的∠1与∠2是邻补角吗?为什么?【教师强调】邻补角的特点:①顶点相同;②有一条公共边,另一边互为反向延长线;③成对出现。(2)下列各图中∠1、∠2是对顶角吗?【教师强调】对顶角的特点:①顶点相同;②角的两边互为反向延长线;③成对出现的。(3)请分别画出下图中∠1的对顶角和∠2的邻补角.学习目标2:掌握对顶角的性质并会推导问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?1.动手操作,推出性质已知,直线AB与CD相交于O点(如图),试猜想∠1、∠3的大小关系,并借助量角器或其他方式验证你的想法.答:∠1=∠3.思考:你能用说理的方法推出∠1=∠3吗?解: ∠1与∠2互补,∠3与∠2互补(邻补角定义),∴∠l=∠3(同角的补角相等).或写成: ∠1=180°-∠2,∠3=180°-∠2(邻补角定义),∴∠1=∠3(等量代换).教师提醒:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而填邻补角定义.2.性质归纳:对顶角相等.3.初步应用例1:如图,直线a、b相交,∠1=40º,求∠2,∠3,∠4的度数.解: ∠1=∠3(对顶角相等),∠1=40º(已知)∴∠3=40º.又 ∠1+∠2=180º(邻补角定义),∠1=40º(已知)∠2=∠4(对顶角相等).∴∠4=∠2=180º-∠1=140º.4.变式练习学生活动:让学生把例题中∠1=40°这个条件换成其他条件,而结论不变,自编几道题.变式1:把∠l=40°变为∠2-∠1=40°.变式2:把∠1=40°变为∠2是∠l的3倍.变式3:把∠1=40°变为∠1:∠2=2:9.三、巩固训练,熟练技能1.(1)若∠1与∠2是对顶角,∠1=16º,则∠2=______º;(2)若∠3与∠4是邻补角,则∠3+∠4=______º.2.若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3=_____º.4231DCBA3.如图,直线AB、CD相交于点O,若∠AOD=2AOC∠,则∠BOD=________.四、归纳总结,板书设计五、课后作业,目标检测。教学反思成功之处:本节课是在七年级上册学过线、角的有关知识的基础上,进一步研究两直线位置关系的第一课时.对顶角是几何求解、证明中的一个基本图形,其中对顶角相等也是证明中常用的结论,以此实现角之间的相互转化.内容相对简单,但又非常重要。对顶角的概念出来后,立即找到...