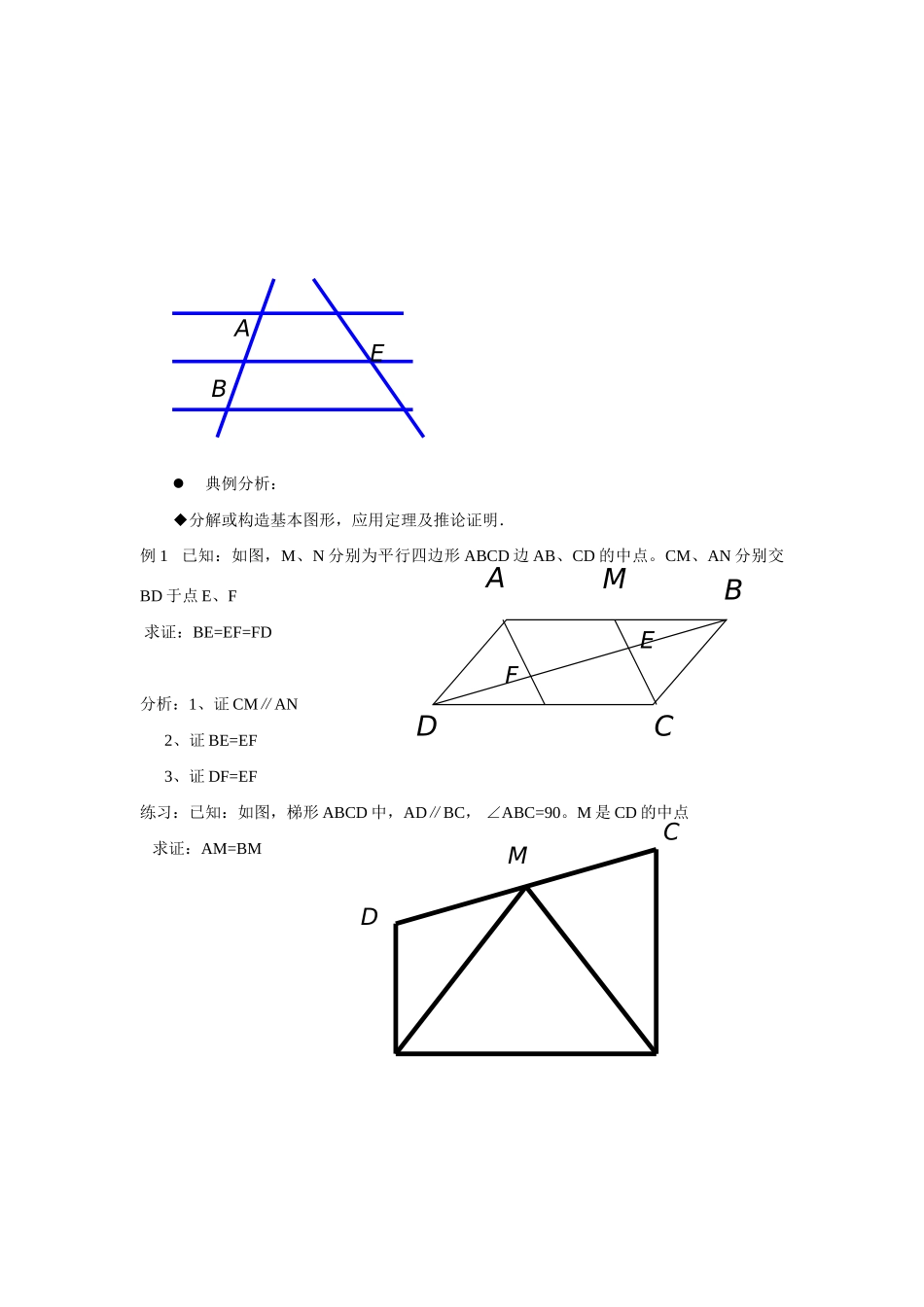
《平行线分线段定理》导学案学习目标:1.了解平行线分线段定理产生的背景,体验定理的产生过程;2.探索并理解平行线分线段定理的证明过程;3.能独立证明平行线分线段定理的推论 1、推论 2;4.能应用定理和推论解决相关的几何计算问题和证明问题;重、难点:重点:掌握平行线分线段定理以及推论;难点:定理和推论的应用;学习过程:一、课前准备:1)预习教材第二页至第五页的内容,从中找出疑惑之处;2)回忆初中学习过的平行线的判定和性质;二、新课导学:知识梳理:平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段 推论 1:经过三角形一边的中点与另一边平行的直线必 推论 2:经过梯形一腰的中点,且与底边平行的直线 基础自测:判断题1.如图△ABC 中点 D、E 三等分 AB,DF∥EG∥BC,DF、EG 分别交 AC 于点 F、G,则点 F、G 三等分 AC( ) A 2.四边形 ABCD 中,点 M、N 分别在 AB、CD 上若 AM=BM、DN=CN 则 AD∥MN∥BC ( )3.一组平行线,任意相邻的两平行线间的距离都相等,则这组平行线能等分线段。 ( )4.如图l1∥l2∥l3且AB=BC,那么AB=BC=DE=EF ( ) DBEFCGCDFl3l2l1典例分析:◆分解或构造基本图形,应用定理及推论证明. 例 1 已知:如图,M、N 分别为平行四边形 ABCD 边 AB、CD 的中点。CM、AN 分别交BD 于点 E、F 求证:BE=EF=FD 分析:1、证 CM∥AN 2、证 BE=EF 3、证 DF=EF练习:已知:如图,梯形 ABCD 中,AD∥BC, ∠ABC=90。M 是 CD 的中点 求证:AM=BM ABEABMEFCDCDM例 2 如图 4-85. AB⊥j 于 B. CD⊥j 于 C,E 为 AD 中点.求证:△EBC 是等腰三角形. 分析:先分析图中存在哪些基本图形,然后怎样利用它们的结论解题.练习:如图 4-86,CB⊥AB,DA⊥AB,M 为 CD 中点.求证:∠MAB=∠MBA.AB◆ n 等分任意一已知线段的作图例 3 已知:线段AB,求作:线段AB的五等分点引申:问题1: 求作一点P把线段AB分成2:3问题2: 如果把△ABC 的面积分成2:3怎么办?分析:引导学生构造定理的基本图形,进行作图和证明,强调平行线组要分别经过点 A 和点 B.◆达标检测,回授效果 1.已知:如图 11,在梯形 ABCD 中,AB//CD,E 是 CD 的中点, EF//BC 交 AB 于 F,FG// BD 交 AD 于 G。 求证:AG = DG。 2.如图 12,在△ABC 中,D 是 AB 的中...