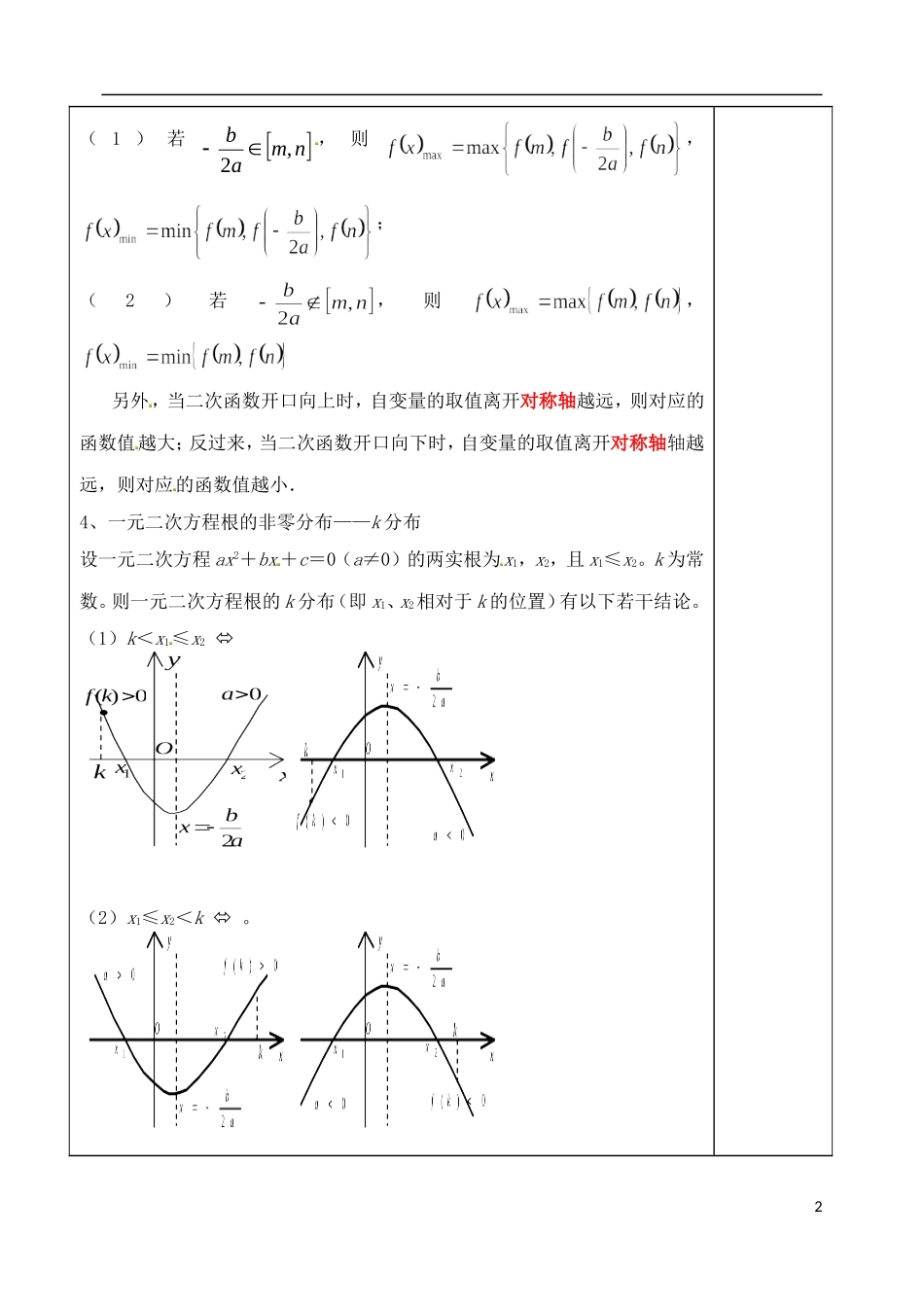
山东省泰安市肥城市第三中学高考数学一轮复习二次函数幂函数教案学习内容学习指导、即时感悟学习目标:理解二次函数的概念,熟练掌握二次函数的图像和性质.能结合二次函数的图像,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系。通过具体实例了解幂函数的图象和性质,并能进行简单的应用.学习重点:二次函数的性质和应用,二次函数根的分布和恒成立等问题学习难点:二次函数的性质和应用,二次函数根的分布和恒成立等问题回顾﹒预习1、二次函数的三种表示方法:(1)一般式(2)顶点式(3)两根式2、二次函数y=ax2+bx+c(a≠0)有如下性质:二次函数(a>0)图像△>0△=0[来源:学科网]△<0与x轴的交点对称轴顶点坐标单调区间二次函数(a<0)图像△>0△=0△<0与x轴的交点[来源:Zxxk.Com]对称轴顶点坐标单调区间3、二次函数在区间上的最值问题。设,则二次函数在闭区间上的最大、最小值有二次函数的图像与性质1(1)若nmab,2,则,;(2)若,则,另外,当二次函数开口向上时,自变量的取值离开对称轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开对称轴轴越远,则对应的函数值越小.4、一元二次方程根的非零分布——k分布设一元二次方程ax2+bx+c=0(a≠0)的两实根为x1,x2,且x1≤x2。k为常数。则一元二次方程根的k分布(即x1、x2相对于k的位置)有以下若干结论。(1)k<x1≤x2(2)x1≤x2<k。2特殊地①x1<0<x2ac<0。②x1<1<x2a(a+b+c)<0。5、幂函数:定义域、值域、单调性、定点基础自测1、函数f(x)=x2-2x+2的单调增区间是()(A)[1,+∞),(B)(-∞,-1)(C)[-1,+∞),(D)以上都不对2、函数的定义域为,那么其值域为()A.B.C.D.3、已知一个二次函数的顶点的坐标为(0,4),且过点(1,5),这个二次函数的解析式为4、利用函数的性质,判断下列两个值的大小3[来源:学科网]在第Ⅰ象限单调[来源:学科网]在第Ⅰ象限单调在第Ⅰ象限单调在第Ⅰ象限单调在第Ⅰ象限单调(,)(,)(,)(,)(,)(1)(2)(3)[来源:学科网]自主﹒合作﹒探究例1:求在区间上的最大值和最小值解:f(x)=x^2-2ax-1=(x-a)^2-a^2-1对称轴是x=a当a≤0时,最大值为f(2)=3-4a;最小值为f(0)=-1当0<a≤1时,最大值为f(2)=3-4a;最小值为f(a)=-a^2-1当1<a≤2时,最大值为f(0)=-1;最小值为f(a)=-a^2-1当a>2时,最大值为f(0)=-1;最小值为f(0)=-a^2-1例3、关于的方程有两个实根,(1)若一个大于1,一个小于1,求的取值范围;(2)若都大于1,求的取值范围;(3)若在(0,1)内,求的取值范围;(4)若一个大于0,一个小于0求的取值范围;有两个实数根,则有:=4(m+3)^2-4(2m+14)=4m^2+24m+36-8m-56=4m^2+16m-20>=0m^2+4m-5>=0(m+5)(m-1)>=0m>=1或者m<=-5一根比4大,另一根比4小,则有:f(4)<0即:4^2+2(m+3)*4+2m+14<016+8m+24+2m+14<010m<-54m<-5.4结合图像①对称轴与区间的关系,对称轴在区间左侧、右侧、在区间内②当在区间内时看距离与端点的远近[来源:学科网][来源:Zxxk.Co4综上所述,m<-5.4例3、已知幂函数是偶函数,且在区间上是减函数.(1)求函数的解析式;(2)讨论的奇偶性.解析:(1)为偶函数,则m²-2m-3为偶数,在区间(0,正无穷)上是单调减函数,则有m²-2m-3<0,即-1