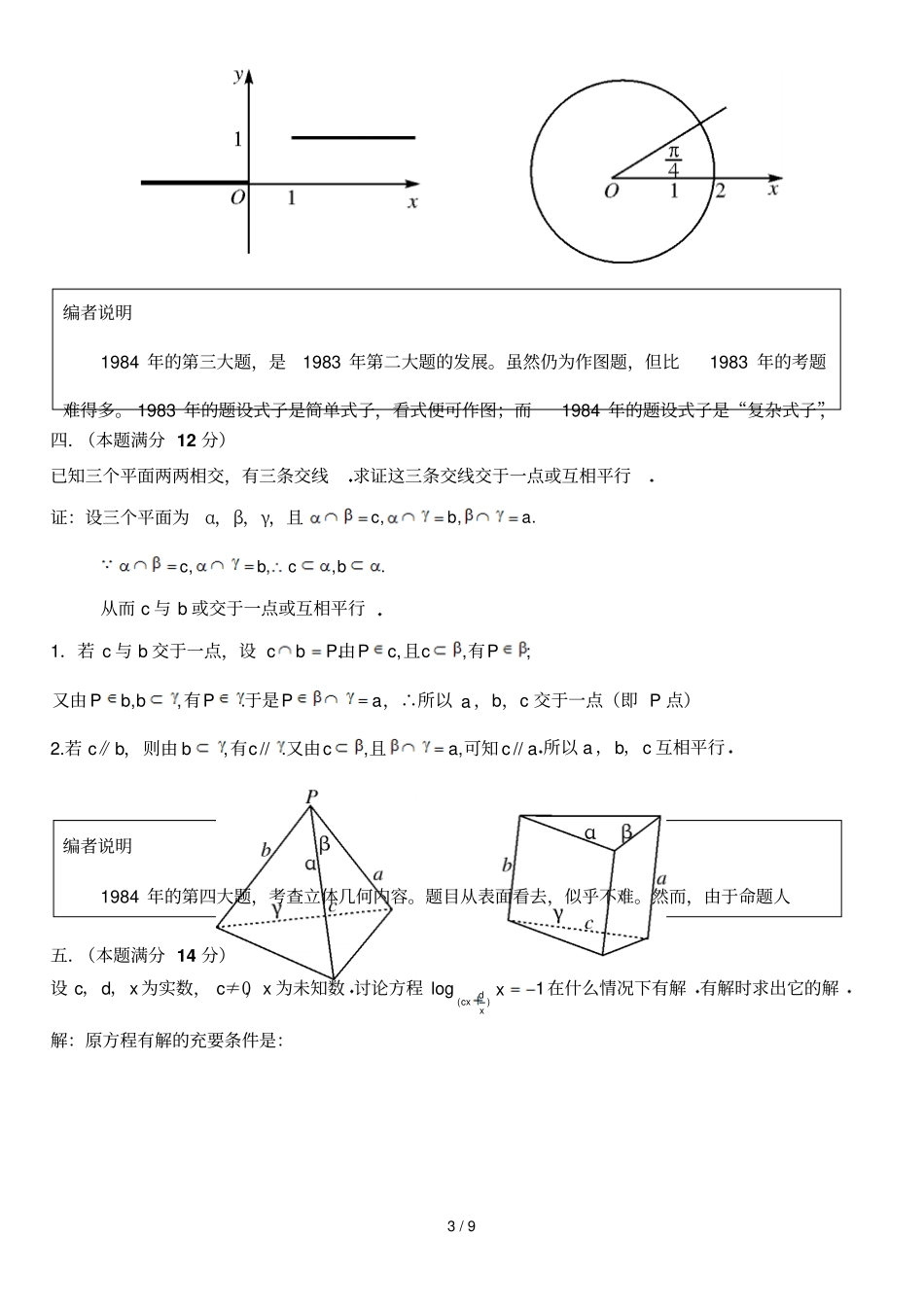
1/9编者说明数学试题选择题,同上一年,即1983年一样多,也是5道小题,但考生感到比上年难得多。有的考生拿到第1小题就不能动笔。首先是因为1984年对选择题的考题要求很严。第一次也是唯一一次提出“得负分”的评分要求。数学月刊七月号创难度之最的1984年普通高等学校招生全国统一考试理科数学试题(这份试题共八道大题,满分120分第九题是附加题,满分10分,不计入总分)一.(本题满分15分)本题共有5小题,每小题选对的得3分;不选,选错或多选得负1分1.数集X={(2n+1)π,n是整数}与数集Y={(4k1)π,k是整数}之间的关系是(C)(A)XY(B)XY(C)X=Y(D)X≠Y2.如果圆x2+y2+Gx+Ey+F=0与x轴相切于原点,那么(C)(A)F=0,G≠0,E≠0.(B)E=0,F=0,G≠0.(C)G=0,F=0,E≠0.(D)G=0,E=0,F≠0.3.如果n是正整数,那么)1]()1(1[812nn的值(B)(A)一定是零(B)一定是偶数(C)是整数但不一定是偶数(D)不一定是整数4.)arccos(x大于xarccos的充分条件是(A)(A)]1,0(x(B))0,1(x(C)]1,0[x(D)]2,0[x5.如果θ是第二象限角,且满足,sin12sin2cos那么2(B)(A)是第一象限角(B)是第三象限角(C)可能是第一象限角,也可能是第三象限角(D)是第二象限角二.(本题满分24分)本题共6小题,每一个小题满分4分只要求直接写出结果)1.已知圆柱的侧面展开图是边长为2与4的矩形,求圆柱的体积答:.84或2.函数)44(log25.0xx在什么区间上是增函数?答:x<-2.3.求方程21)cos(sin2xx的解集编者说明1984年,是中国高考改革有创意的一年。就在这一年,数学命题组提出了高考“出活题,考基础,考能力”的命题指导思想。自1977年恢复高考以来,高考命题基本上是“模仿命题”,模仿课本上的例习题,模仿教参上的参考题,考场上出现了“解题有套”的现象,高校传出了“高分低能”的说法。2/9编者说明1984年的第二大题,含6个小题,比1983年的2个小题多出了4个,从而使整个试卷的题量比1983年多出了3道。题目很活,题量又大,多数考生在规定的时间不能完成解答,这也是1984年数学得分很低的原因之一。答:},12|{},127|{ZnnxxZnnxx4.求3)2||1|(|xx的展开式中的常数项答:-205.求1321limnnn的值答:06.要排一张有6个歌唱节目和4个舞蹈节目的演出节目单,任何两个舞蹈节目不得相邻,问有多少种不同的排法(只要求写出式子,不必计算)答:!647P三.(本题满分12分)本题只要求画出图形1.设,0,1,0,0)(xxxH当当画出函数y=H(x-1)的图象2.画出极坐标方程)0(0)4)(2(的曲线解(1)(2)解:1.2.3/9编者说明1984年的第三大题,是1983年第二大题的发展。虽然仍为作图题,但比1983年的考题难得多。1983年的题设式子是简单式子,看式便可作图;而1984年的题设式子是“复杂式子”,编者说明1984年的第四大题,考查立体几何内容。题目从表面看去,似乎不难。然而,由于命题人四.(本题满分12分)已知三个平面两两相交,有三条交线求证这三条交线交于一点或互相平行证:设三个平面为α,β,γ,且.,,abc.,,,bcbc从而c与b或交于一点或互相平行1.若c与b交于一点,设;,,.PccPPbc有且由aPPbbP于是有又由.,,,∴所以a,b,c交于一点(即P点)2.若c∥b,则由acaccb//,,.//,可知且又由有所以a,b,c互相平行五.(本题满分14分)设c,d,x为实数,c≠0,x为未知数讨论方程1log)(xxdcx在什么情况下有解有解时求出它的解解:原方程有解的充要条件是:4/9编者说明1984年的第五题,考查对数函数。具体考查对数方程的有解条件。然而设计“创新到了对数底数”,使得一直看惯了“底数只为单一字母”的考生不知所云。(4))((3),0(2),0(1),01xxdcxxdcxxdcxx由条件(4)知1)(xdcxx,所以12dcx再由c≠0,可得.12cdx又由1)(xdcxx及x>0,知0xdcx,即条件(2)包含在条件(1)及(4)中再由条件(3)及1)(xdcxx,知.1x因此,原条件可简化为以下的等价条件组:(6).1x(5)1,x(1),02cdx由条件(1)(6)知.01cd这个不等式仅在以下两种情形下成立:①c>0,1-d>0,即c>0,d<1;②c<0,1-d<0,即c<0,d>1.再由条件(1)(5)及(6)可知dc1从而,当c>0,d<1且dc1时,或者当c<0,d>1且dc1时,原方程...