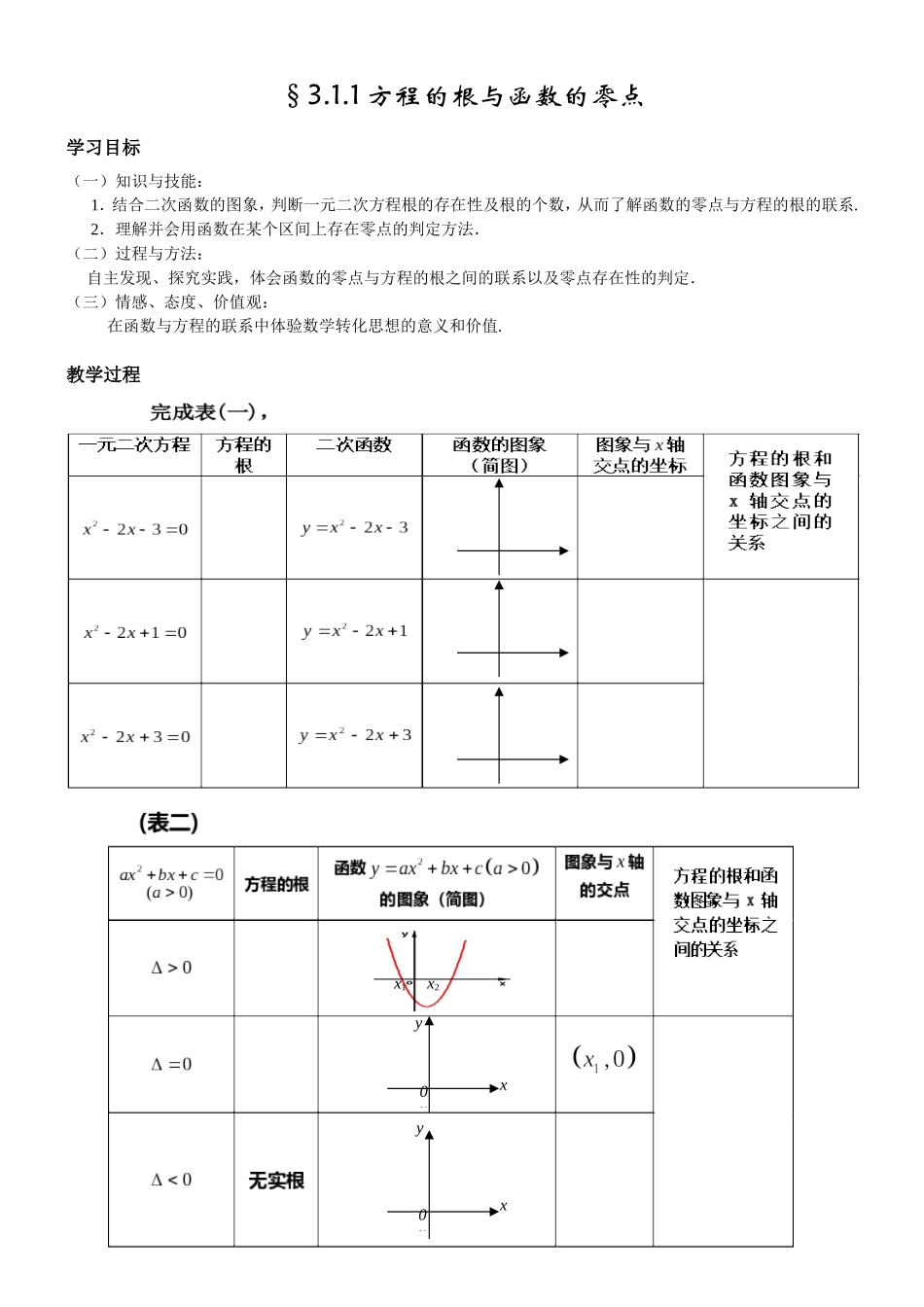
§3.1.1方程的根与函数的零点学习目标(一)知识与技能:1.结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程的根的联系.2.理解并会用函数在某个区间上存在零点的判定方法.(二)过程与方法:自主发现、探究实践,体会函数的零点与方程的根之间的联系以及零点存在性的判定.(三)情感、态度、价值观:在函数与方程的联系中体验数学转化思想的意义和价值.教学过程x1x2xy0xxy0x1.函数的零点的定义对于函数,我们把叫做的零点.2、沙场点兵(2)、求下列函数的零点.①②(4)求函数的零点个数.3小组活动把绳子的一端固定在P点,另一端在直线上Q点或M点,并随意摆放绳子,探究以下问题:(1)另一端在Q点时,绳子在[a,b]上是否与x轴一定有交点?(2)另一端在M点时,绳子在[a,b]上是否与x轴一定有交点?(3)把绳子看作是函数在[a,b]上的图象,函数图象的端点在什么情况下,函数必存在零点?(4)如何用f(a)、f(b)的值刻画(3)中的情况?(5)剪断绳子,(3)中的结论是否还成立?4、零点存在性定理新知:如果函数在区间,上的图像是,并且满足,那么函数在区间,内有零点,即存在,,使得,这个也就是方程的根.5、例题讲解例1、求函数的零点个数.6、新知应用,巩固深化(1)、已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:x1234567f(x)239-711-5-12-26那么函数在区间[1,6]上的零点至少有()A.5个B.4个C.3个D.2个(2)、方程x3+3x-5=0一定存在根的区间为()A.(–2,0)B.(0,1)C.(1,2)D.(2,3)7、我的收获8、作业布置:1、课本P88练习12、(1)、函数的零点所在的大致区间是()(2)、若方程在内恰有一解,则的取值范围是()