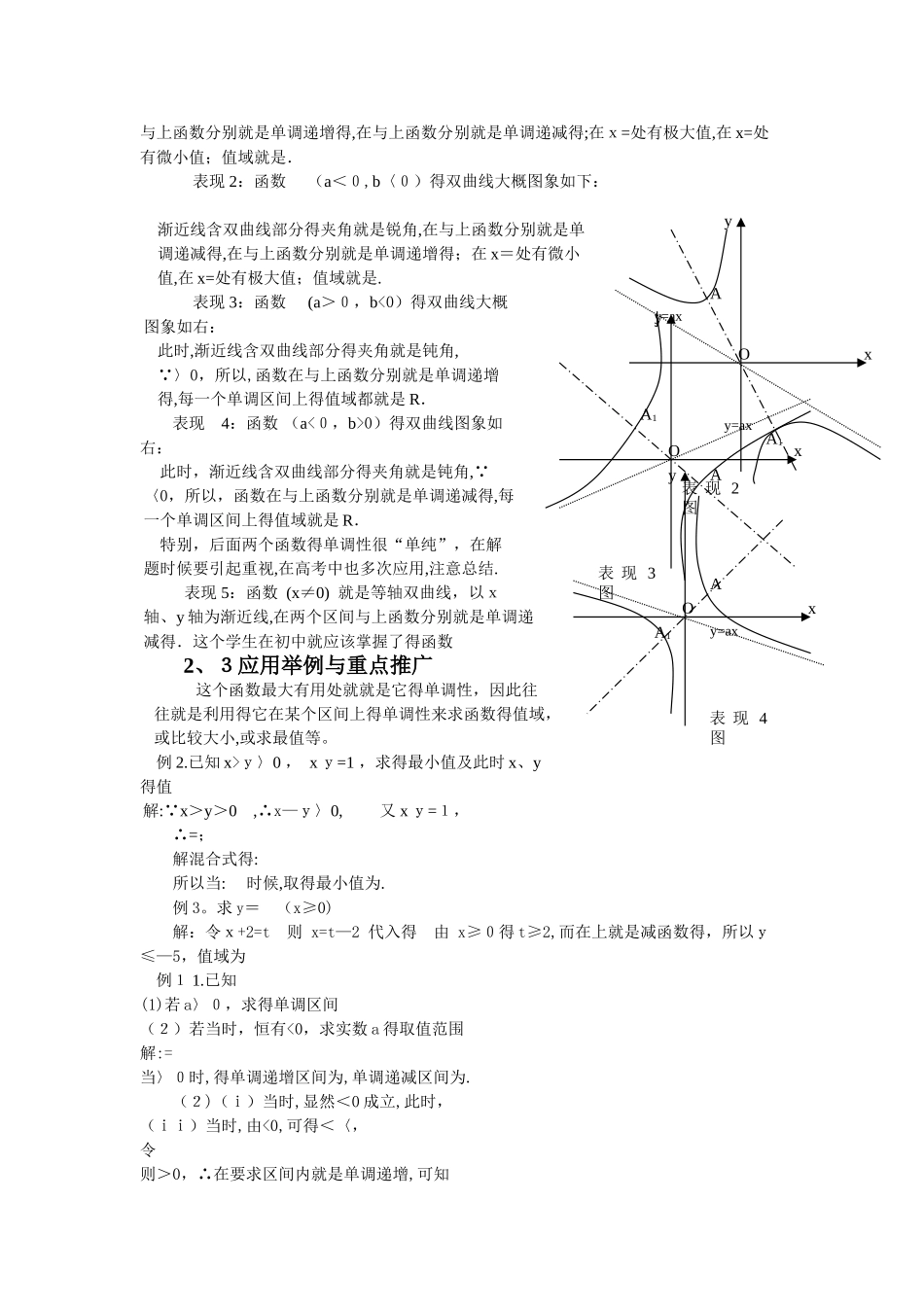
一个十分重要得函数得图象与性质应用 新课标高一数学在“基本不等式”一节课中已经隐含了函数得图象、性质与重要得应用,就是高考要求范围内得一个重要得基础知识.那么在高三第一轮复习课中,对于重点中学或基础比较好一点学校得同学而言,我们务必要系统介绍学习(ab≠0)得图象、性质与应用。2.1 定理:函数(ab≠0)表示得图象就是以 y=a x 与 x=0(y 轴)得直线为渐近线得双曲线。首先,我们根据渐近线得意义可以理解:a x得值与得值比较,当很大很大得时候, 得值几乎可以忽略不计,起决定作用得就是ax得值;当得值很小很小,几乎为0得时候,ax 得值几乎可以忽略不计,起决定作用得就是得值.从而,函数(ab≠0)表示得图象就是以y=a x 与 x=0(y 轴)得直线为渐近线得曲线.另外我们可以发现这个函数就是奇函数,它得图象应该关于原点成中心对称.由于函数形式比较抽象,系数都就是字母,因此要证明曲线就是双曲线就是很麻烦得,我们通过一个例题来说明这一结论.例 1.若函数就是双曲线,求实半轴 a,虚半轴 b,半焦距 c,渐近线及其焦点,并验证双曲线得定义。 分析:画图,曲线如右所示;由此可知它得渐近线应该就是与 x=0 两条直线;由此,两条渐近线得夹角得平分线 y=x 就就是实轴了,得出顶点为 A(,3),A1(-,—3); ∴ a==, 由渐近线与实轴得夹角就是 30º,则有=ta n30º, 得 b=2 , c==4, ∴ F1(2,)F 2(-2,-)。为了验证函数得图象就是双曲线,在曲线上任意取一点P(x, )满足即可;所以,函数表示得曲线就是双曲线.(在许多地方,老师把这个曲线形状形象概括为“双钩曲线”,其实很不准确得.)2。2五种表现形式表现 1:函数 (a>0,b〉0)得双曲线大概图象如下:渐近线含双曲线部分得夹角就是锐角,在OxyAA1例1图OxyAA1y=ax表 现 1图与上函数分别就是单调递增得,在与上函数分别就是单调递减得;在x=处有极大值,在 x=处有微小值;值域就是.表现 2:函数 (a<0,b〈0)得双曲线大概图象如下:渐近线含双曲线部分得夹角就是锐角,在与上函数分别就是单调递减得,在与上函数分别就是单调递增得;在 x=处有微小值,在 x=处有极大值;值域就是.表现 3:函数 (a>0,b<0)得双曲线大概图象如右:此时,渐近线含双曲线部分得夹角就是钝角, 〉0,所以,函数在与上函数分别就是单调递增得,每一个单调区间上得值域都就是 R.表现 4:函数 (a<0,b>0)得双曲线图象如右:此时,...