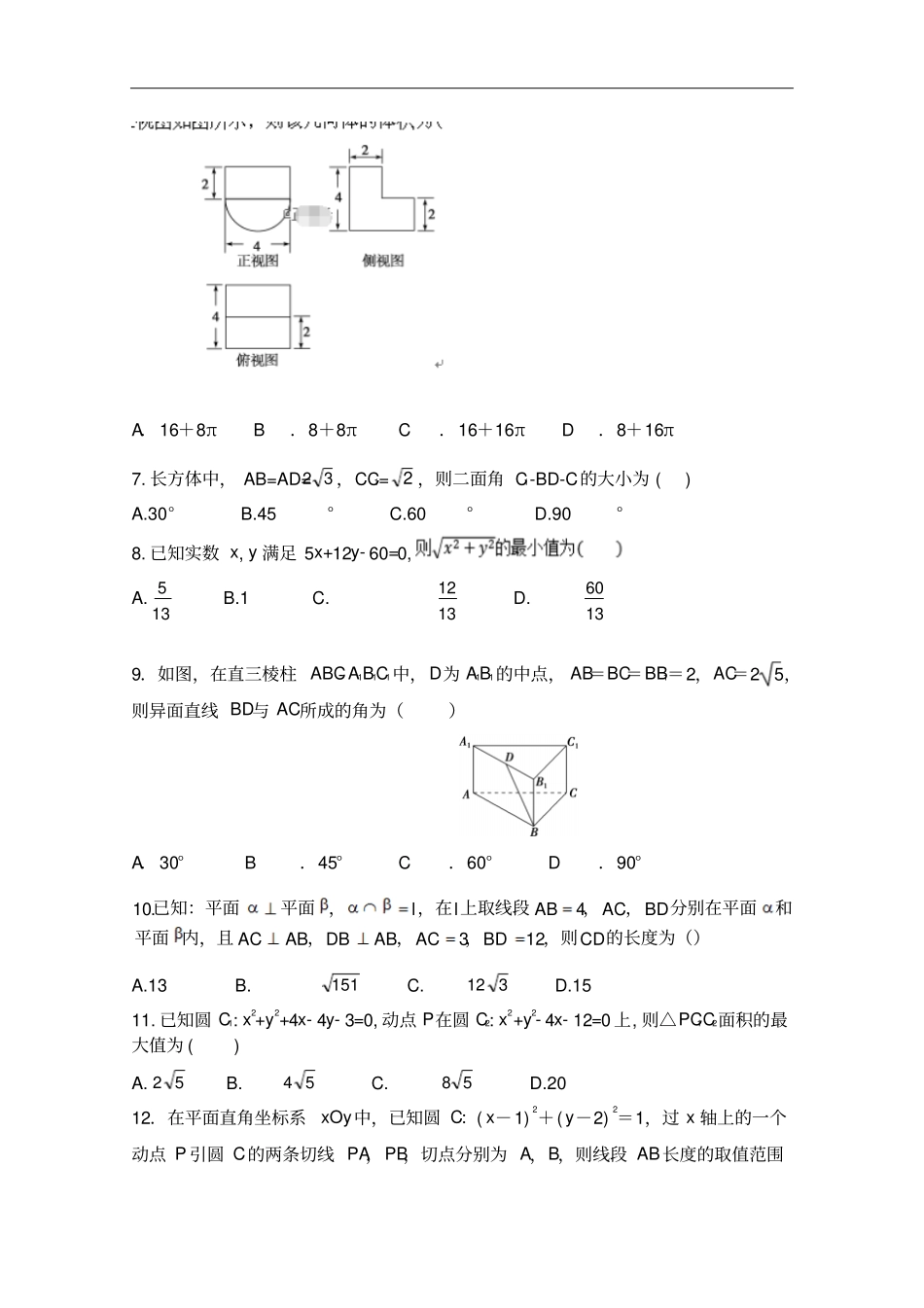
宁夏银川市兴庆区长庆高级中学2019-2020学年高一上学期期末考试数学试卷满分:150分时间:120分钟一.选择题:(每题只有一个正确答案,每题5分,共60分)1.对两条不相交的空间直线a与b,必存在平面α,使得()A.ba,B.//,baC.ba,D.ba,2.已知点A(1,),B(-1,3),则直线AB的倾斜角是()A.60°B.30°C.120°D.150°3.如图,A′B′C′D′为各边与坐标轴平行的正方形ABCD的直观图,若A′B′=3,则原正方形ABCD的面积是()A.9B.3C.94D.364.过点P(4,-1),且与直线3x-4y+6=0垂直的直线方程是()A.4x+3y-19=0B.4x+3y-13=0C.3x+4y-16=0D.3x+4y-8=05.直线x+y-1=0被圆(x+1)2+y2=3截得的弦长等于()A.2B.2C.22D.46.某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π7.长方体中,AB=AD=32,CC1=2,则二面角C1-BD-C的大小为()A.30°B.45°C.60°D.90°8.已知实数x,y满足5x+12y-60=0,A.135B.1C.1312D.13609.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=BB1=2,AC=25,则异面直线BD与AC所成的角为()A.30°B.45°C.60°D.90°的长度为(),则,,,内,且平面和分别在平面,,上取线段,在,平面已知:平面CDBDACABDBABACBDACABll1234.10A.13B.151C.312D.1511.已知圆C1:x2+y2+4x-4y-3=0,动点P在圆C2:x2+y2-4x-12=0上,则△PC1C2面积的最大值为()A.52B.54C.58D.2012.在平面直角坐标系xOy中,已知圆C:(x-1)2+(y-2)2=1,过x轴上的一个动点P引圆C的两条切线PA,PB,切点分别为A,B,则线段AB长度的取值范围是()A.(3,2)B.[3,2)C.(3,2]D.[3,2]二.填空题(每题5分,共20分)13.过点P(3,4)在两坐标轴上截距相等的直线方程为______________.14.已知a,b表示直线,α,β,γ表示平面.①则若,,,baba;②内任意一条直线,则垂直于若aa,;③baba,则,,若;④////,则,,若baba.上述命题中,正确命题的序号是________.15.点P(-2,-1)到直线l:(1+3λ)x+(1+2λ)y=2+5λ的距离为d,则d的取值范围是16.已知正三棱柱的底面边长为,为的中点,平面与平面所成的锐二面角的正切值是,则四棱锥外接球的表面积为________.三.解答题(共70分)17.(本小题满分10分)已知某几何体的俯视图是矩形(如图),正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.18.(本小题满分12分)直线l经过两直线l1:3x+4y-2=0和l2:2x+y+2=0的交点.(1)若直线l与直线3x+y-1=0平行,求直线l的方程;(2)点A(3,1)到直线l的距离为5,求直线l的方程.19.(本小题满分12分)设圆C的方程为x2+y2-4x-5=0,(1)求该圆的圆心坐标及半径.(2)若此圆的一条弦AB的中点为P(3,1),求直线AB的方程.20.(本小题满分12分)如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.(1)求证:DC⊥平面PAC;(2)求证:平面PAB⊥平面PAC;(3)设点E为AB的中点,在棱PB上是否存在点F,使得PA∥平面CEF?并说明理由.21.(本小题满分12分)已知以点C为圆心的圆经过点A(-1,0)和B(3,4),且圆心C在直线x+3y-15=0上.(1)求圆C的标准方程;(2)设点Q(-1,m)(m>0)在圆C上,求△QAB的面积.22.(本小题满分12分)如图(1),在矩形ABCD中,已知AB=2,AD=22,M,N分别为AD和BC的中点,对角线BD与MN交于O点,沿MN把矩形ABNM折起,使两个半平面所成二面角为60°,如图(2).(1)求证:BO⊥DO;(2)求AO与平面BOD所成角的正弦值.数学答案一.选择题1-5:BCABB6-10:AADCA11-12:BB二.填空题13.xy34或x+y-7=014.②④15.0≤d<1316.19三.解答题17.解:(1)几何体的体积V=S矩形h=×6×8×4=64.(2)正侧面及相对侧面底边上的高h1==5.左、右侧面的底边上的高h2==4.故几何体的侧面积S=2·×8×5+=22440.18.解:由3x+4y-2=0,2x+y+2=0,解得x=-2,y=2,所以两直线的交点M(-2,2).(1)设直线l的方程为3x+y+c=0(c≠-1),把点(-2,2)代入方程,得c=4,所以直线l的方程为3x+y+4=0.(2)当直线l的斜率不存在时,直线方程为x=-2,此时点A(3,1)到直线l的...