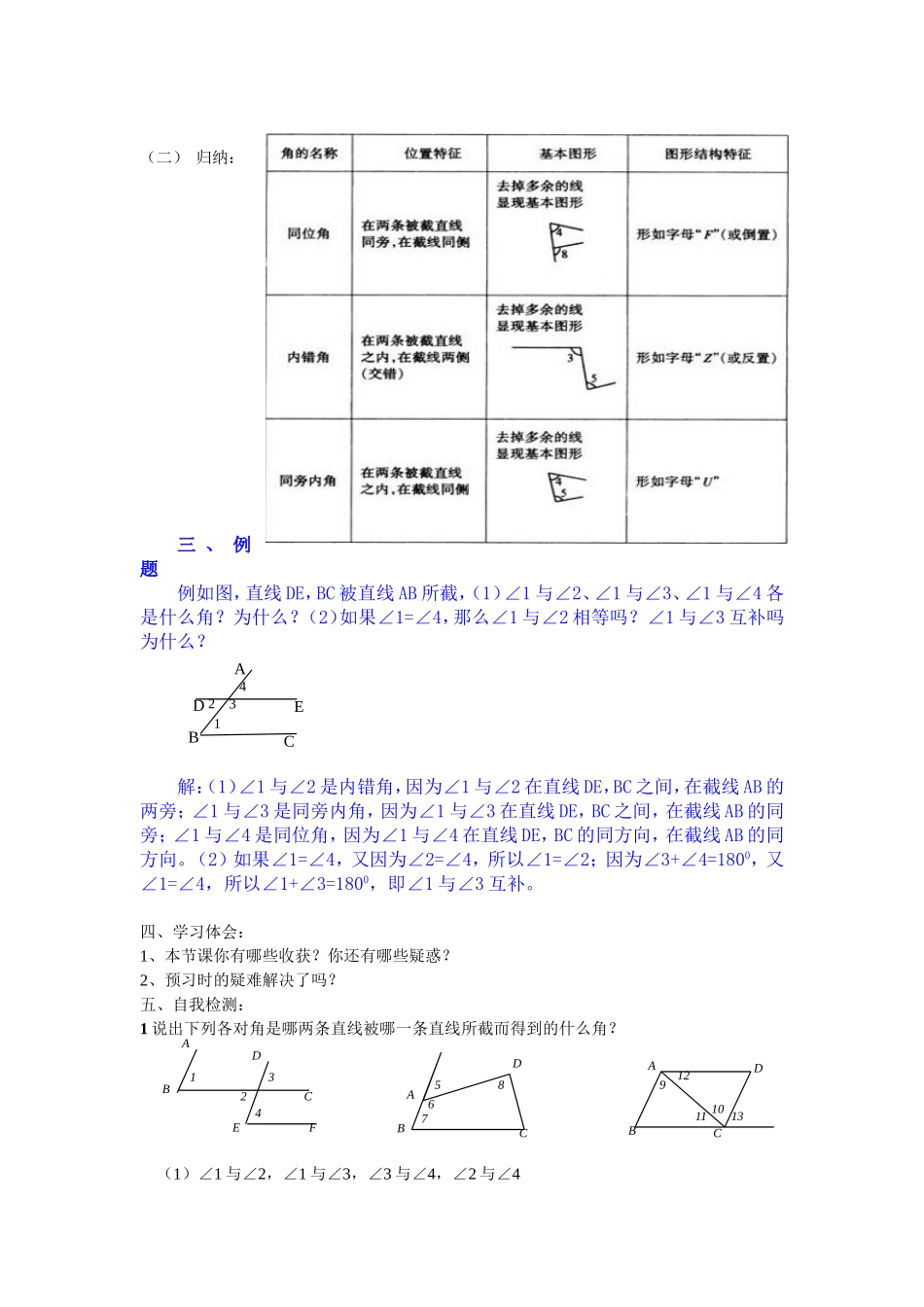
5.1.3同位角、内错角、同旁内角主备:南苑学习目标:1、理解同位角、内错角、同旁内角的意义。2、会熟练地识别图中的同位角、内错角、同旁内角。3、培养学生分析、抽象、归纳能力,培养学生的识图能力学习重点:同位角、内错角、同旁内角的识别。学习难点:较复杂图形中同位角、内错角、同旁内角的识别。学习过程:一、自主探究1、预习疑难:。2、直线AB、CD相交于O小于平角的角有几个?有几对对顶角?有几对邻补角?二、探索与思考如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截)构成个角。我们来研究其中没有公共顶点的两个角的关系。(一)同位角1、定义:如图1,∠1和∠5,分别在直线AB、CD的,在直线EF的。具有这种位置关系的一对角叫做同位角。2、请你找出图中还有哪几对角构成同位角。3、两条直线被第三条直线所截构成的八个角中,共有对同位角。(二)内错角(1)1、定义:如图2,∠3和∠5,分别在直线AB、CD的,在直线EF的。具有这种位置关系的一对角叫做内错角。2、请你找出图中还有哪几对角构成内错角。3、两条直线被第三条直线所截构成的八个角中,共有对内错角(三)同旁内角1、定义:如图2,∠3和∠6,分别在直线AB、CD的,在直线EF的。具有这种位置关系的一对角叫做同旁内角。(2)2、请你找出图中还有哪几对角构成同旁内角。3、两条直线被第三条直线所截构成的八个角中,共有对同旁内角(四)总结:(1)以上三对角都有一边公共,是第三条直线(截线).(2)识别“第三条直线(两个角一边所在的同一直线)”是关键.三、应用(一)例如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?(二)变式训练:找出图中所有的同位角、内错角、同旁内角。EF(二)归纳:三、例题例如图,直线DE,BC被直线AB所截,(1)∠1与∠2、∠1与∠3、∠1与∠4各是什么角?为什么?(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗为什么?解:(1)∠1与∠2是内错角,因为∠1与∠2在直线DE,BC之间,在截线AB的两旁;∠1与∠3是同旁内角,因为∠1与∠3在直线DE,BC之间,在截线AB的同旁;∠1与∠4是同位角,因为∠1与∠4在直线DE,BC的同方向,在截线AB的同方向。(2)如果∠1=∠4,又因为∠2=∠4,所以∠1=∠2;因为∠3+∠4=1800,又∠1=∠4,所以∠1+∠3=1800,即∠1与∠3互补。四、学习体会:1、本节课你有哪些收获?你还有哪些疑惑?2、预习时的疑难解决了吗?五、自我检测:1说出下列各对角是哪两条直线被哪一条直线所截而得到的什么角?(1)∠1与∠2,∠1与∠3,∠3与∠4,∠2与∠431BD4ACE2BACDEF1234ABCD5768ABCD129101113(2)∠5与∠8,∠5与∠7,∠6与∠7,∠6与∠8(3)∠9与∠10,∠11与∠12,∠9与∠11,∠10与∠12,∠B与∠132、如图(3),直线、被所截,∠1与∠2是内错角,直线、被所截,∠1与∠B是同位角;直线、被所截,∠3和∠B是同位角。3、如右图所示:(1)∠1,∠2,∠3,∠4,∠5,∠6是直线、被第三条直线所截而成的。(2)∠2的同位角是,∠1的同位角是。(3)∠3的内错角是,∠4的内错角是。(4)∠6的同旁内角是,∠5的同旁内角是,(5)∠4与∠A是同旁内角吗?为什么?4.如图,将长方形纸片折叠后再展开,折痕的夹角是多少?反思:本节课首先通两条直线相交的位置关系到三条直线相交自然、直接的引入了新课,,让学生通过自己回顾发现,充分发挥学生的积极性、主动性和创造性。这些问题设计的目的是深化教学重点,而后通过细致入微的师生共同学习同位角的概念及结构特征,能使学生更好的理解概念以及判别这类角。而在内错角与同旁内角的学习则由学生通过类比学习感受。之后的双手比划,让学生既动手又动脑,实验体会,在活动中加深对概念的理解.习题的选择也是采用趣味知识竞赛的方式,激发了学生的求知欲,起到了巩固新知的作用。最后,用表格式小结完善知识结构,而学生也能清楚明了本节课所应掌握的知识。BCFED123A图(3)ABCEF134562