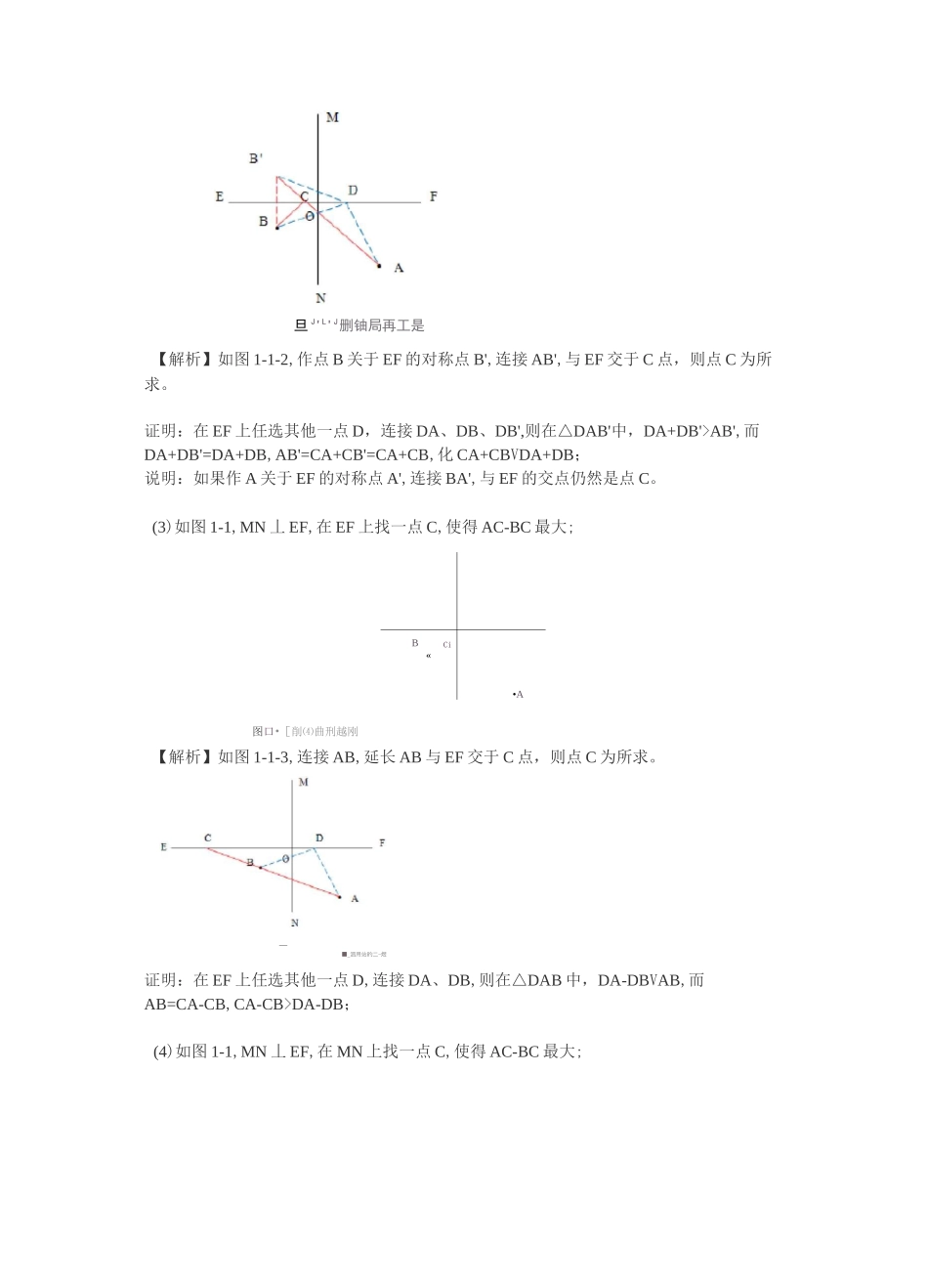
轴对称与折叠问题(适合初一学生)(—)几何作图最值模型模型一:直角坐标系下的几何最值1.两条线段的和差最值问题:(1)如图1-1,MN丄EF,在MN上找一点C,使得AC+BC最小;【解析】如图1-1-1,连接AB,与MN交于C点,则点C为所求。证明:在MN上任选其他一点D,连接DA、DB,则在△DAB中,DA+DB>AB,AB=CA+CB,・•・CA+CBVDA+DB;(2)如图1-1,MN丄EF,在EF上找一点C,使得AC+BC最小;旦J'L'J删铀局再工是【解析】如图1-1-2,作点B关于EF的对称点B',连接AB',与EF交于C点,则点C为所求。证明:在EF上任选其他一点D,连接DA、DB、DB',则在△DAB'中,DA+DB'>AB',而DA+DB'=DA+DB,AB'=CA+CB'=CA+CB,化CA+CBVDA+DB;说明:如果作A关于EF的对称点A',连接BA',与EF的交点仍然是点C。(3)如图1-1,MN丄EF,在EF上找一点C,使得AC-BC最大;BCi«•A图口•[削⑷曲刑越刚【解析】如图1-1-3,连接AB,延长AB与EF交于C点,则点C为所求。■_泗用站旳二-煜证明:在EF上任选其他一点D,连接DA、DB,则在△DAB中,DA-DBVAB,而AB=CA-CB,CA-CB>DA-DB;(4)如图1-1,MN丄EF,在MN上找一点C,使得AC-BC最大;图1-L-3M0*B*AB0■*A圈1-1【解析】如图1-1-4,作点A关于MN的对称点A',连接A'B,延长线与MN交于C点,则点C为所求。证明:在MN上任选其他一点D,连接DA、DB、DA',则在△DA'B中,DA'-DBVA'B,而DA'-DB=DA-DB,A'B=CA'-CB=CA-CB,CA-CB>DA-DB;说明:如果作B关于MN的对称点B',连接AB',延长线与MN的交点仍然是点C。2,三条线段之和的最值问题:(1)如图1-2-1-1,MN丄EF,在EF上找一点C,MN上找一点D,使得丨AC+CD+BDI最小;【解析】如图1-2-1-2,分别作A关于EF的对称点A'和B关于MN的对称点B',连接A'B',分别与EF、MN交于C、D两点,则点C、D为所求。证明:分别在EF、MN任取其他两点P、Q,连接PQ、PA、PA'、QB、QB',则在点A'和点B'之间,A'B'最短,而AC+CD+BD=A'C+CD+DB'=A'B';PA+PQ+QB=A'P+PQ+QB'>A'B',・•・AC+CD+BDVPA+PQ+QB。(2)如图1-2-2-1,等腰直角AABC中,AB=BC,ZABC=90°,点E为AB边上一点,将AABC沿AC翻折至AADC,在AC上求作一点P,使得APBE的周长最短。【解析】因为BE的长度已经固定,实际上是求作点P,使得PE+PB最小。如图1-2-2-2,点D是点B关于AC的对称点,连接DE,与AC相交于点P,则点P为所求。证明:取AC上其他任一点Q,则QB+QE=QE+QD>DE=PE+PD=PE+PB,故PE+PB+BEVQB+QE+BEo(此题与1(2)类似)模型二:含平行线的多线段之和的几何最值如图2-1,直线a〃b.A、B为两定点,M、N分别在直线a、b上,且MN丄a,请确定M、N的位置,使得AM+MN+NB最小。【解析】如图2-2,过A作AE丄a,并截取AE=MN,连接BE,与b交于N,过N作NM丄a,与a交于M点。则M、N为所求的两点。证明:如图2-2,设MN平移至PQ的位置,则因为AE=PQ,且AE〃PQ,所以四边形AEQP为平行四边形,即AP=EQ;同样,AM=EN,AM+BN=BE,在厶BQE中,BQ+QE>BE,所以BQ+AP>BN+AM,两边同时加上PQ和MN,得:BQ+PQ+AP〉BN+MN+AM。模型三:一个角内多线段之和的最值1,如图3-1,点P为ZAOB内部的一点,试分别在OA、OB上各找一点M、N,使厶PMN的周长最小。【解析】如图3-2,分别作P关于OA、OB的对称点P「P2,连接P]P2,与OA、OB分别交于点M、N,则M、N两点为所求。证明:因为PM=MP],NP=NP2,所以△PMN的周长为P]P2;分别在OA、OB上任选其他两点C、D,连接PC、PD、P]C、P2D、CD,贝9CP=CP],DP=DP2,所以APCD的周长为P]C+CD+DP2,而在P1P2两点之间,P]P2的线段最短,故P1P2