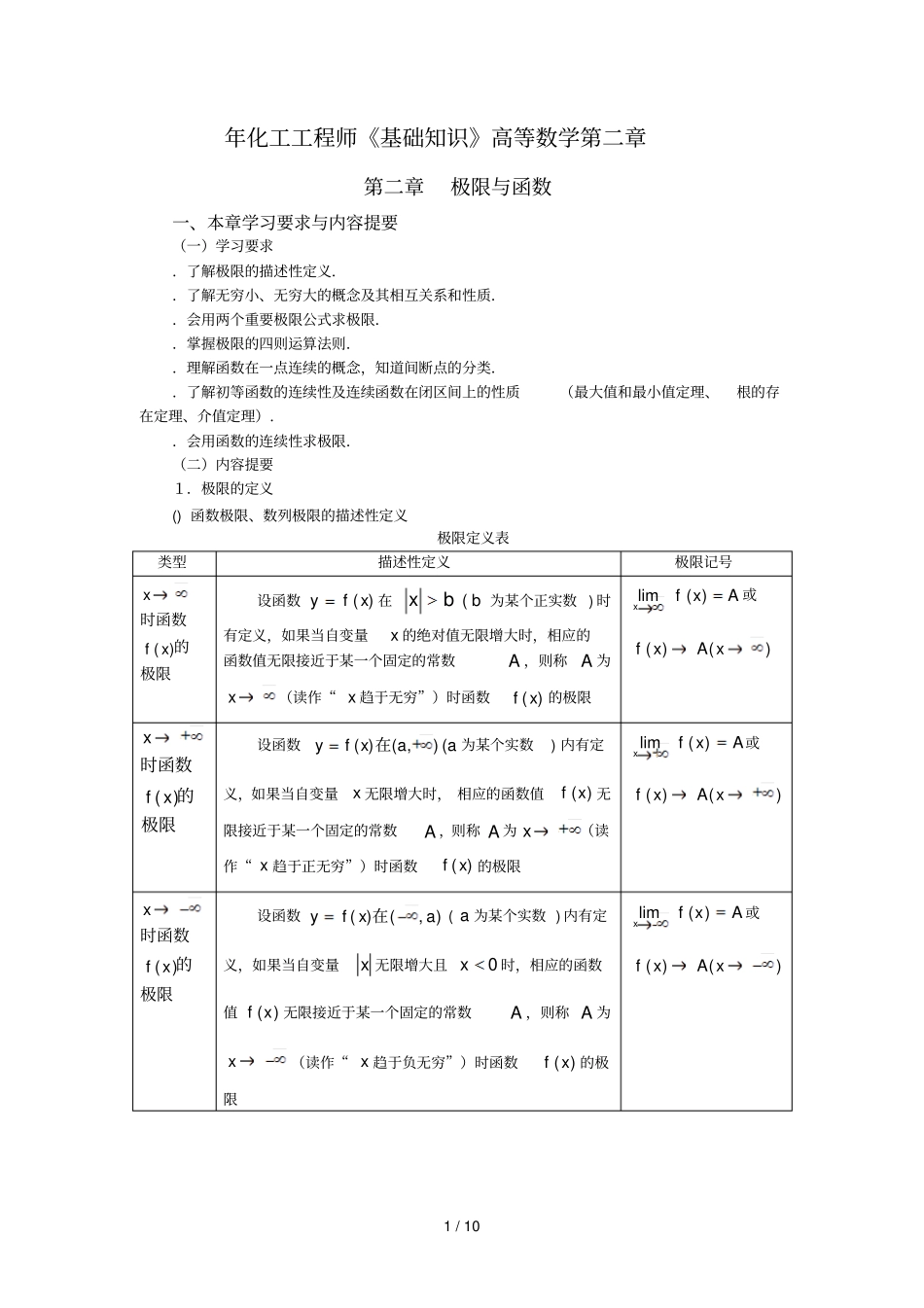
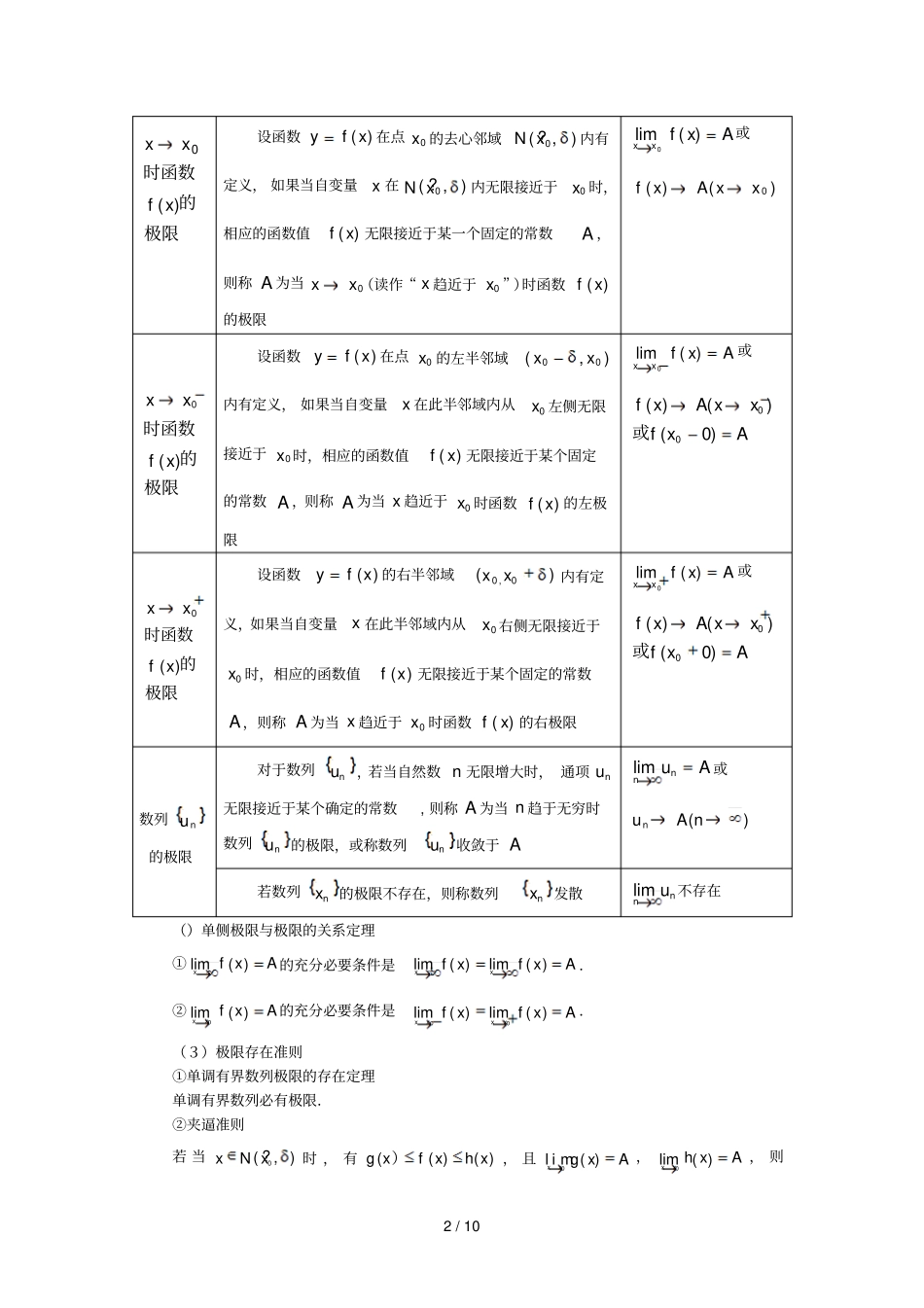
1/10年化工工程师《基础知识》高等数学第二章第二章极限与函数一、本章学习要求与内容提要(一)学习要求.了解极限的描述性定义..了解无穷小、无穷大的概念及其相互关系和性质..会用两个重要极限公式求极限..掌握极限的四则运算法则..理解函数在一点连续的概念,知道间断点的分类..了解初等函数的连续性及连续函数在闭区间上的性质(最大值和最小值定理、根的存在定理、介值定理)..会用函数的连续性求极限.(二)内容提要1.极限的定义()函数极限、数列极限的描述性定义极限定义表类型描述性定义极限记号极限的时函数)(xfx设函数)(xfy在bxb(为某个正实数)时有定义,如果当自变量x的绝对值无限增大时,相应的函数值无限接近于某一个固定的常数A,则称A为x(读作“x趋于无穷”)时函数)(xf的极限Axfx)(lim或)()(xAxf极限的时函数)(xfx设函数aaxfy(),()(在为某个实数)内有定义,如果当自变量x无限增大时,相应的函数值)(xf无限接近于某一个固定的常数A,则称A为x(读作“x趋于正无穷”)时函数)(xf的极限Axfx)(lim或)()(xAxf极限的时函数)(xfx设函数),()(axfy在(a为某个实数)内有定义,如果当自变量x无限增大且0x时,相应的函数值)(xf无限接近于某一个固定的常数A,则称A为x(读作“x趋于负无穷”)时函数)(xf的极限Axfx)(lim或)()(xAxf2/10极限的时函数)(0xfxx设函数)(xfy在点0x的去心邻域),?(0xN内有定义,如果当自变量x在),?(0xN内无限接近于0x时,相应的函数值)(xf无限接近于某一个固定的常数A,则称A为当0xx(读作“x趋近于0x”)时函数)(xf的极限Axfxx)(lim0或)()(0xxAxf极限的时函数)(0xfxx设函数)(xfy在点0x的左半邻域),(00xx内有定义,如果当自变量x在此半邻域内从0x左侧无限接近于0x时,相应的函数值)(xf无限接近于某个固定的常数A,则称A为当x趋近于0x时函数)(xf的左极限Axfxx)(lim0或AxfxxAxf)0()()(00或极限的时函数)(0xfxx设函数)(xfy的右半邻域)(0,0xx内有定义,如果当自变量x在此半邻域内从0x右侧无限接近于0x时,相应的函数值)(xf无限接近于某个固定的常数A,则称A为当x趋近于0x时函数)(xf的右极限Axfxx)(lim0或AxfxxAxf)0()()(00或数列nu的极限对于数列nu,若当自然数n无限增大时,通项nu无限接近于某个确定的常数,则称A为当n趋于无穷时数列nu的极限,或称数列nu收敛于AAunnlim或)(nAun若数列nx的极限不存在,则称数列nx发散nnulim不存在()单侧极限与极限的关系定理①Axfx)(lim的充分必要条件是)(limxfxAxfx)(lim.②Axfxx)(lim0的充分必要条件是)(lim0xfxxAxfxx)(lim0.(3)极限存在准则①单调有界数列极限的存在定理单调有界数列必有极限.②夹逼准则若当),?(0xNx时,有)()((xhxfxg),且Axgxx)(lim0,Axhxx)(lim0,则3/10Axfxx)(lim0..极限的四则运算法则设)(lim0xfxx及)(lim0xgxx都存在,则())(lim)(lim)()(lim000xgxfxgxfxxxxxx;())(lim)(lim)()(lim000xgxfxgxfxxxxxx,)(lim)(lim00xfCxCfxxxx(C为任意常数);())()(lim)()(lim00xgxfxgxfxxxx)0)(lim(0xgxx.上述极限四则运算法则对自变量的其他变化过程下的极限同样成立..两个重要极限(),1sinlim0xxx一般形式为1)()(sinlim0)(xuxuxu(其中)(xu代表x的任意函数).(),11limexxx一般形式为e)()()(11limxuxuxu(其中)(xu代表x的任意函数).4.无穷小量与无穷大量(1)无穷小量在自变量的某个变化过程中,以零为极限的变量称为该极限过程中的无穷小量,简称无穷小.例如,如果0)(lim0xfxx,则称当0xx时,)(xf是无穷小量.注意一般说来,无穷小表达的是变量的变化状态,而不是变量的大小,一个变量无论多么小,都不能是无穷小量,数零是惟一可作为无穷小的常数.(2)无穷大量在自变量的某个变化过程中,绝对值可以无限增大的变量称为这个变化过程中的无穷大量,简称无穷大.应该注意的是:无穷大量是极限不存在的一种情形,我们借用极限的记号)(lim0xfxx,表示“当0xx时,)(xf是无穷大量”.(3)无穷小量与无穷大量的关系在自变量的某个变化过程中,无穷大量的倒数是无穷小量,非零无穷小量的倒数是无穷大量.(4)无穷小量的运算4/10①有限个无穷小量的代数和是无穷小量.②有限个无穷...