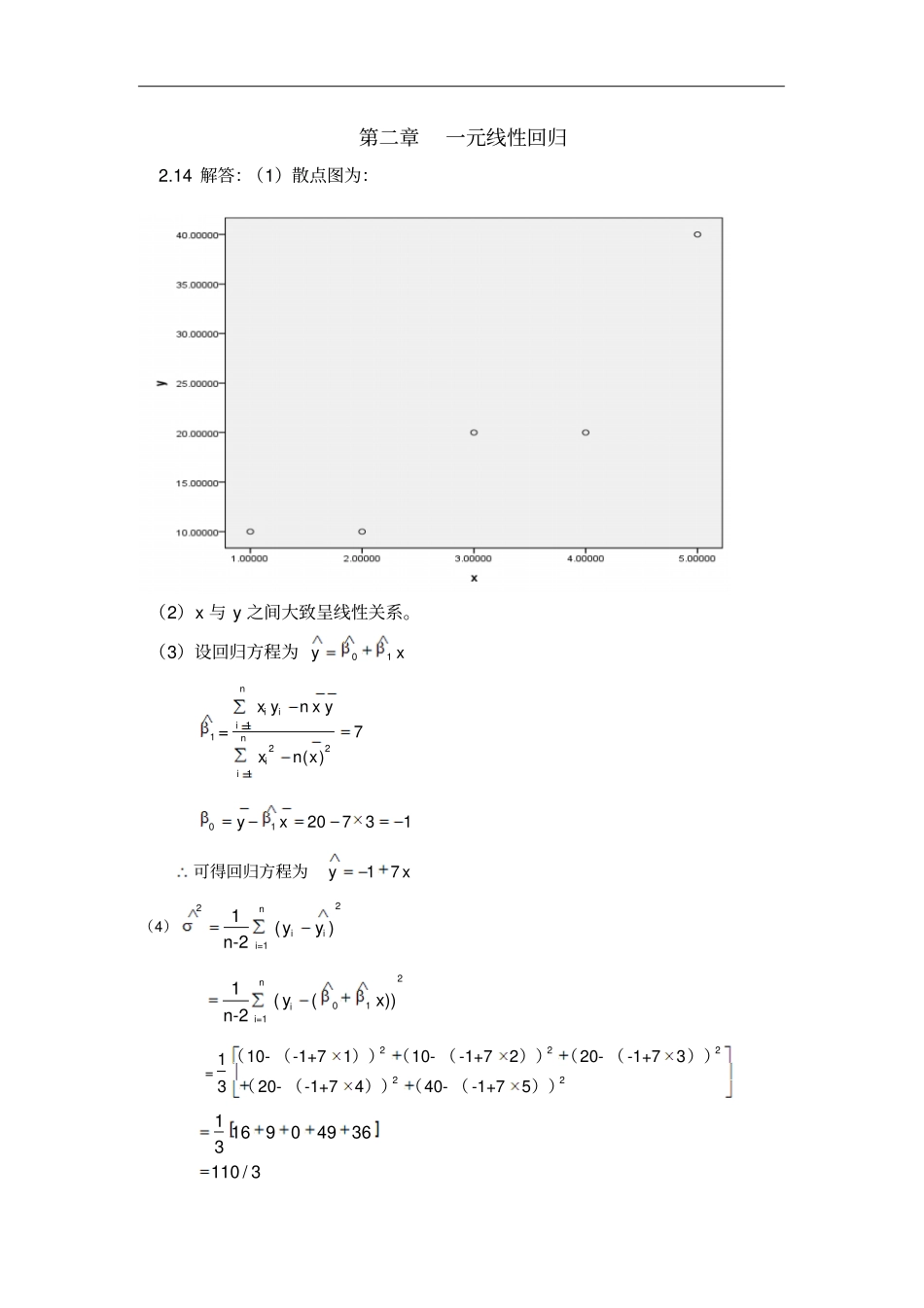
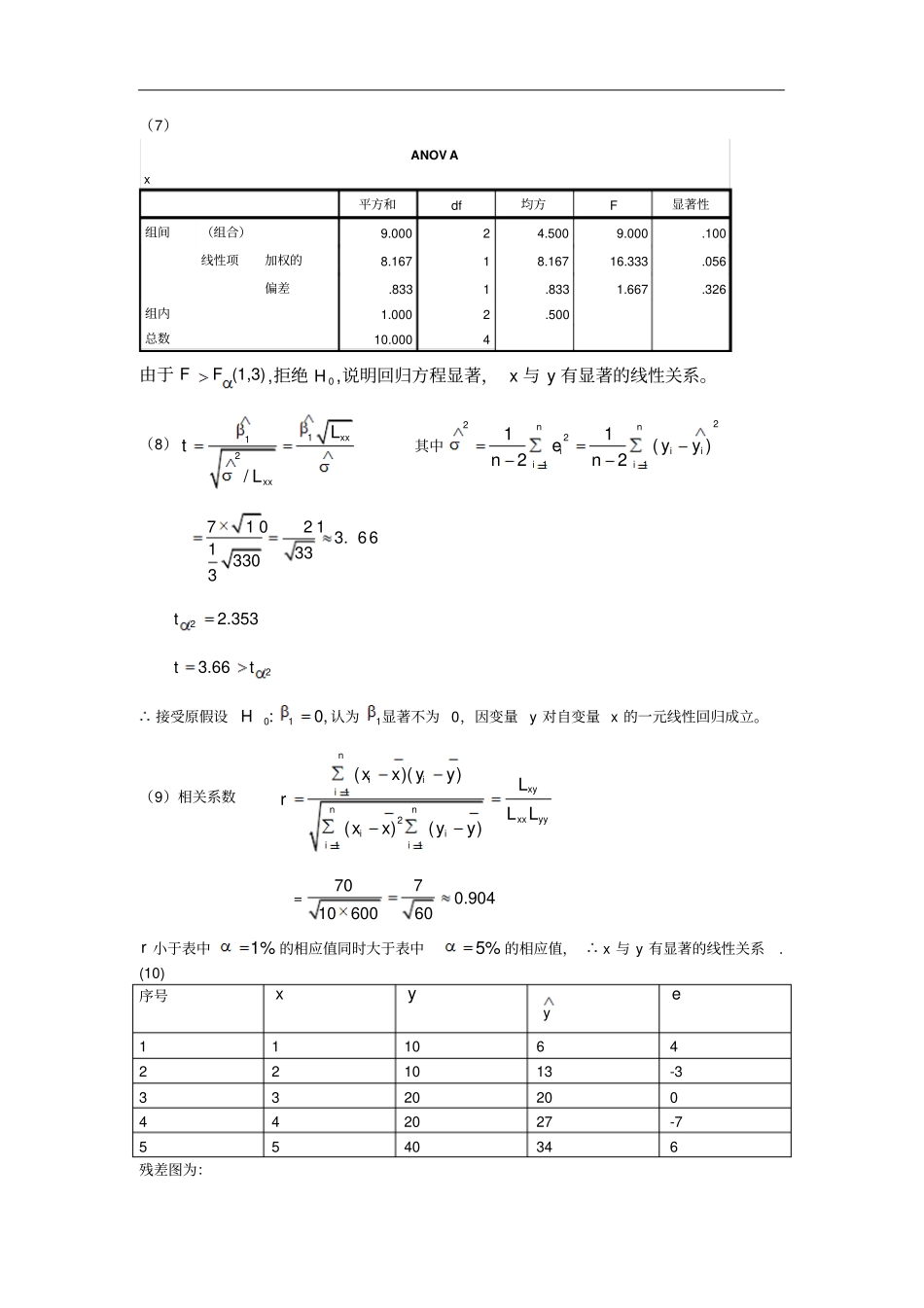
第二章一元线性回归2.14解答:(1)散点图为:(2)x与y之间大致呈线性关系。(3)设回归方程为01yx1=12217()niiiniixynxyxnx0120731yx17yx可得回归方程为(4)22ni=11()n-2iiyy2n01i=11(())n-2iyx=2222213(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75))1169049363110/313306.13(5)由于211(,)xxNL1112()/xxxxLtL服从自由度为n-2的t分布。因而1/2()||(2)1xxLPtn也即:1/211/2()xxxxpttLL=1可得11195%333333的置信度为的置信区间为(7-2.353,7+2.353)即为:(2.49,11.5)22001()(,())xxxNnL00002221()1()()xxxxtxxnLnL服从自由度为n-2的t分布。因而00/22||(2)11()xxPtnxnL即220/200/21()1()()1xxxxxxpttnLnL可得195%7.77,5.77的置信度为的置信区间为()(6)x与y的决定系数22121()490/6000.817()niiniiyyryy(7)ANOVAx平方和df均方F显著性组间(组合)9.00024.5009.000.100线性项加权的8.16718.16716.333.056偏差.8331.8331.667.326组内1.0002.500总数10.0004由于(1,3)FF,拒绝0H,说明回归方程显著,x与y有显著的线性关系。(8)112/xxxxLtL其中2221111()22nniiiiieyynn710213.661333303/22.353t/23.66tt接受原假设01:0,H认为1显著不为0,因变量y对自变量x的一元线性回归成立。(9)相关系数1211()()()()niixyinnxxyyiiiixxyyLrLLxxyy=7070.9041060060r小于表中1%的相应值同时大于表中5%的相应值,x与y有显著的线性关系.(10)序号xyye111064221013-33320200442027-75540346残差图为:从图上看,残差是围绕e=0随机波动,从而模型的基本假定是满足的。(11)当广告费0x=4.2万元时,销售收入028.4y万元,95%置信度为的置信区间y2近似为,即(17.1,39.7)2.15解答:(1)散点图为:(2)x与y之间大致呈线性关系。(3)设回归方程为01yx1=1221(2637021717)0.0036(71043005806440)()niiiniixynxyxnx012.850.00367620.1068yx0.10680.0036yx可得回归方程为(4)22ni=11()n-2iiyy2n01i=11(())n-2iyx=0.23050.4801(5)由于211(,)xxNL1112()/xxxxLtL服从自由度为n-2的t分布。因而1/2()||(2)1xxLPtn也即:1/211/2()xxxxpttLL=1可得195%的置信度为的置信区间为0.4801/12978600.4801/1297860(0.0036-1.860,0.0036+1.860)即为:(0.0028,0.0044)22001()(,())xxxNnL00002221()1()()xxxxtxxnLnL服从自由度为n-2的t分布。因而00/22||(2)11()xxPtnxnL即220/200/21()1()()1xxxxxxpttnLnL可得195%0.3567,0.5703的置信度为的置信区间为()(6)x与y的决定系数22121()()niiniiyyryy16.8202718.525=0.908(7)ANOVAx平方和df均方F显著性组间(组合)1231497.5007175928.2145.302.168线性项加权的1168713.03611168713.03635.222.027偏差62784.464610464.077.315.885组内66362.500233181.250总数1297860.0009由于(1,9)FF,拒绝0H,说明回归方程显著,x与y有显著的线性关系。(8)112/xxxxLtL其中2221111()22nniiiiieyynn0.003612978608.5420.04801/21.895t/28.542tt接受原假设01:0,H认为1显著不为0,因变量y对自变量x的一元线性回归成立。(9)相关系数1211()()()()niixyinnxxyyiiiixxyyLrLLxxyy=46530.9489129786018.525r小于表中1%的相应值同时大于表中5%的相应值,x与y有显著的线性关系.(10)序号xyye18253.53.07680.4232221510.88080.11923107043.95880.0412455022.0868-0.0868548011.8348-0.8348692033.4188-0.4188713504.54.9688-0.466883251.51.27680.2232967032.51880.481210121554.48080.5192从图上看,残差是围绕e=0随机波动,从而模型的基本假定是满足的。(11)0010003.7x新保单时,需要加班的时间为y小时。(12)00/200y(2)1ytnh的置信概率为1-的置信区间精确为,即为(2.7,4.7)近似置信区间为:02y,即(2.74,4.66)(13)可得置信水平为1-的置信区间为0/200(2)ytnh,即为(3.33,4.07).2.16(1)散点图为:可以用直线回归描述y与x之间的关系.(2)回归方程为:12112.6293.314yx(3)从图上可看出,检验误差项服从正态分布。第三章多元线性回归3.11解:(1)用SPSS算出y,x1,x2,x3相关系数矩阵:相关性yx1x2x3Pearson相关性y1.000.556.731.724x1.5561.000.113.398x...