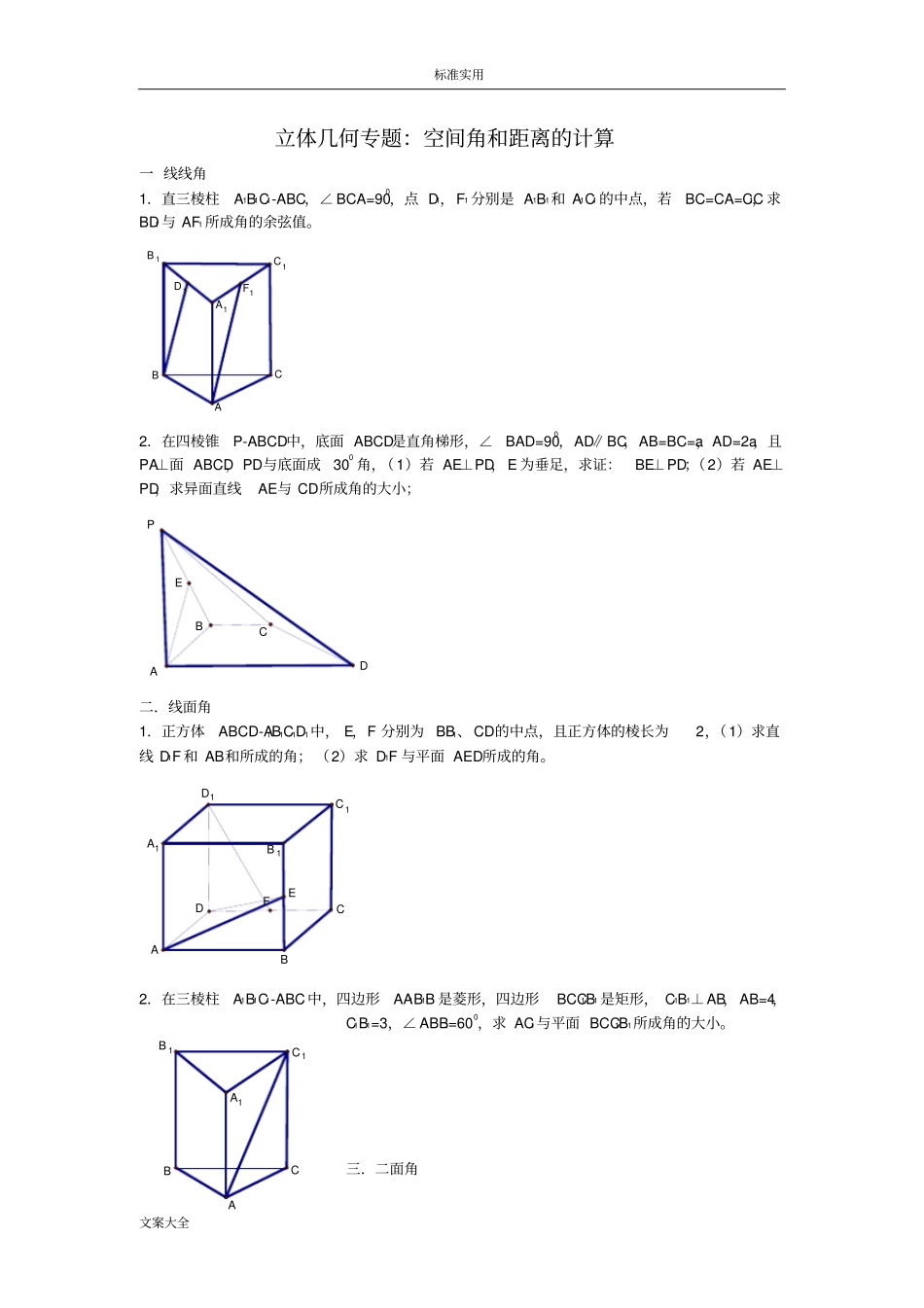
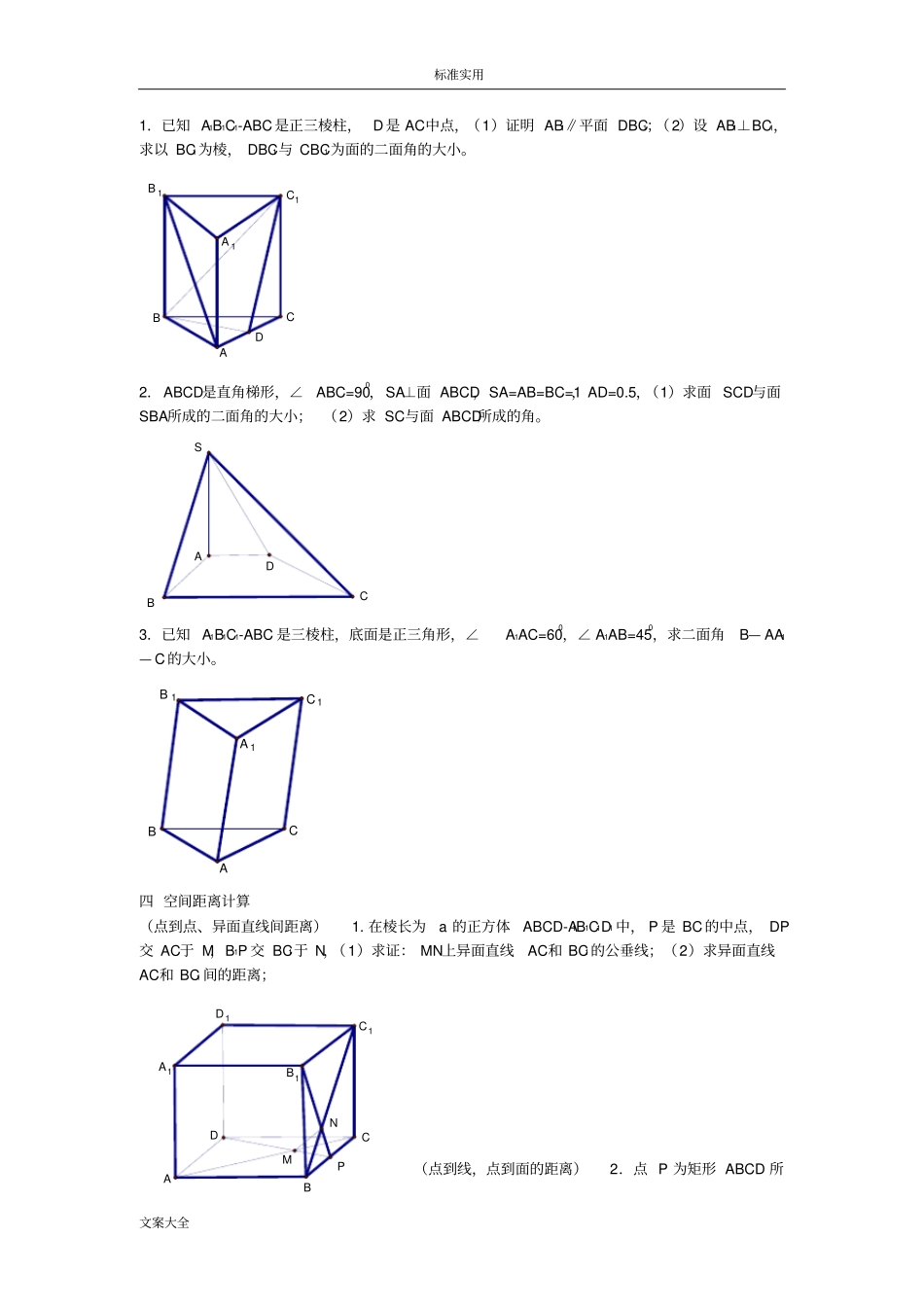
标准实用文案大全立体几何专题:空间角和距离的计算一线线角1.直三棱柱A1B1C1-ABC,∠BCA=900,点D1,F1分别是A1B1和A1C1的中点,若BC=CA=CC1,求BD1与AF1所成角的余弦值。F1D1B1C1A1BAC2.在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=900,AD∥BC,AB=BC=a,AD=2a,且PA⊥面ABCD,PD与底面成300角,(1)若AE⊥PD,E为垂足,求证:BE⊥PD;(2)若AE⊥PD,求异面直线AE与CD所成角的大小;ABCDPE二.线面角1.正方体ABCD-A1B1C1D1中,E,F分别为BB1、CD的中点,且正方体的棱长为2,(1)求直线D1F和AB和所成的角;(2)求D1F与平面AED所成的角。CDEFD1C1B1A1AB2.在三棱柱A1B1C1-ABC中,四边形AA1B1B是菱形,四边形BCC1B1是矩形,C1B1⊥AB,AB=4,C1B1=3,∠ABB1=600,求AC1与平面BCC1B1所成角的大小。三.二面角B1C1A1BAC标准实用文案大全1.已知A1B1C1-ABC是正三棱柱,D是AC中点,(1)证明AB1∥平面DBC1;(2)设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角的大小。DB1C1A1BAC2.ABCD是直角梯形,∠ABC=900,SA⊥面ABCD,SA=AB=BC=1,AD=0.5,(1)求面SCD与面SBA所成的二面角的大小;(2)求SC与面ABCD所成的角。BADCS3.已知A1B1C1-ABC是三棱柱,底面是正三角形,∠A1AC=600,∠A1AB=450,求二面角B—AA1—C的大小。B1C1BACA1四空间距离计算(点到点、异面直线间距离)1.在棱长为a的正方体ABCD-A1B1C1D1中,P是BC的中点,DP交AC于M,B1P交BC1于N,(1)求证:MN上异面直线AC和BC1的公垂线;(2)求异面直线AC和BC1间的距离;(点到线,点到面的距离)2.点P为矩形ABCD所CDNMPD1C1B1A1AB标准实用文案大全在平面外一点,PA⊥面ABCD,Q为线段AP的中点,AB=3,CB=4,PA=2,求(1)点Q到直线BD的距离;(2)点P到平面BDQ的距离;3.边长为a的菱形ABCD中,∠ABC=600,PC⊥平面ABCD,E是PA的中点,求E到平面PBC的距离。(线到面、面到面的距离)4.已知斜三棱柱A1B1C1-ABC的侧面A1ACC1与底面ABC垂直,∠ABC=900,BC=2,AC=23,且AA1⊥A1C,AA1=A1C,(1)求侧棱AA1与底面ABC所成角的大小;(2)求侧面A1ABB1与底面ABC所成二面角的大小;(3)求侧棱B1B和侧面A1ACC1距离;B1C1BACA15.正方形ABCD和正方形ABEF的边长都是1,且平面ABCD、ABFE互相垂直,点M在AC上移动,点N在BF上移动,若CM=NB=a(20a),(1)求MN的长;(2)当a为何值时,MN的长最小;立体几何中的向量问题空间角与距离1.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为.基础自测标准实用文案大全答案45°或135°2.二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为.答案60°3.如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成角的余弦值等于.答案5154.如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO—A′B′C′D′,A′C的中点E与AB的中点F的距离为.答案a225.(2008·福建理,6)如图所示,在长方体ABCD—A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为.答案510例1(2008·海南理,18)如图所示,已知点P在正方体ABCD—A′B′C′D′的对角线BD′上,∠PDA=60°.(1)求DP与CC′所成角的大小;(2)求DP与平面AA′D′D所成角的大小.解如图所示,以D为原点,DA为单位长度建立空间直角坐标系D—xyz.则DA=(1,0,0),CC=(0,0,1).连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.设DH=(m,m,1)(m>0),由已知〈DH,DA〉=60°,由DA·DH=|DA||DH|cos〈DH,DA〉,可得2m=122m.解得m=22,所以DH=(22,22,1).(1)因为cos〈DH,CC〉=2111022022=22,所以〈DH,CC〉=45°,即DP与CC′所成的角为45°.(2)平面AA′D′D的一个法向量是DC=(0,1,0).标准实用文案大全因为cos〈DH,DC〉=2101122022=21,所以〈DH,DC〉=60°,可得DP与平面AA′D′D所成的角为30°.例2在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=23,M、N分别为AB、SB的中点,如图所示.求点B到平面CMN的距离.解取AC的中点O,连接OS、OB....