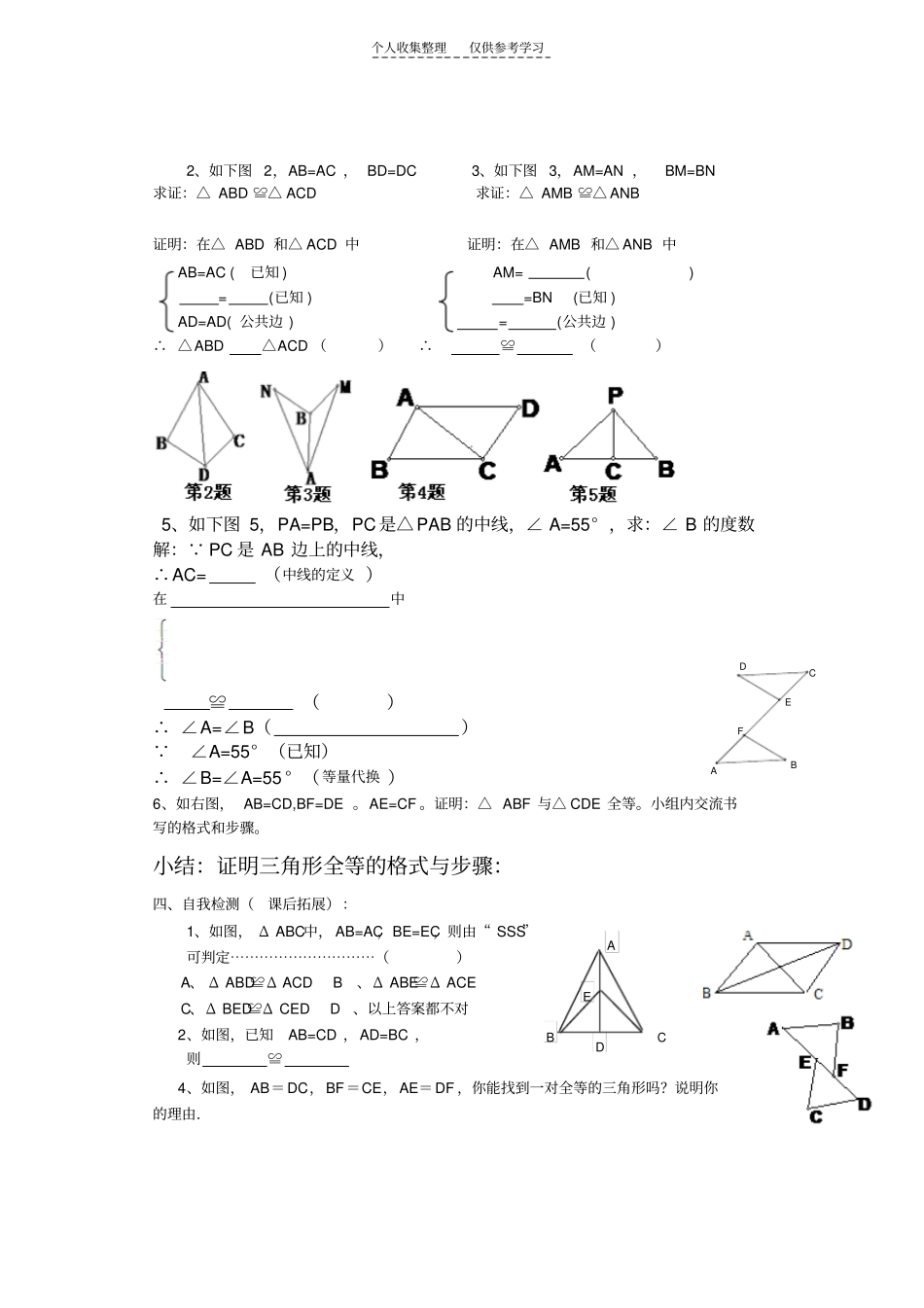
个人收集整理仅供参考学习达县城南学校导学案(宝剑不磨要生锈,人不学习要落后。聪明出于勤奋,天才在于积累)3.三角形全等条件的探索学科:数学年级:七年级主写人:张子军学习小组自我评价:学习目标:1、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;2、掌握三角形的“边边边”条件。3、在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。流程:温故知新探索新知例题研习巩固练习自我检测反思小结重难点:重点:三角形”边边边”的全等条件。难点:用三角形”边边边”的条件进行有条理的思考并进行简单的推理教师活动(环节、措施)温故知新,探索新知,例题研习,巩固练习,自我检测,反思小结,教学后记。)学生活动(自主参与、合作探究、展示交流,总结结论,知识应用,自我检测,课后小结,课后拓展)学具准备:圆规,刻度尺,量角器,硬纸板,小剪刀(或小刀片);一、准备活动:1、全等三角形的__________相等,__________相等.2、如图1,已知△AOC≌△BOD,则∠A=∠B,∠C=_______,______=∠2,对应边有AC=________,______=OB,______=OD.3、如图2,已知△AOC≌△DOB,则∠A=∠D,∠C=_______,______=∠2,对应边有AC=_______,OC=_______,AO=_______.4、如图3,已知∠B=∠D,∠1=∠2,∠3=∠4,AB=CD,AD=CB,AC=CA.则△________≌△___________5、判定两个三角形全等,依定义必须满足()(A)三边对应相等(B)三角对应相等(C)三边对应相等和三角对应相等(D)不能确定二、实验操作:每人都画三角形,并编号,并剪下来在小组内(或与其它组同学)进行比较是否全等,(1)画一个三角形:使一边为10cm(2)画一个三角形:使一角为50o结论:是否全等?结论:是否全等?个人收集整理仅供参考学习(3)画一个三角形:(4)画一个三角形:使其中两个角分别为35o,75o使其中两边分别为9cm,12cm结论:是否全等?结论:是否全等?(5)画一个三角形:(6)画一个三角形:使一边为10cm,一个角为50o使三个角为35o,65o,80o结论:是否全等?结论:是否全等?(7)画一个三角形:使三边为10cm,13cm,16cm作图方法:(保留作图痕迹)先画一线段AB,使得AB=10cm,再分别以A、B为圆心,13cm、16cm为半径画弧,?两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=105cm,AC=13cm,BC=15cm.结论:____________________________________________________.归纳:三边对应相等的两个三角形,简写为“”或“”.若用数学语言表述:如右图在△ABC和'''ABC中, ''ABABACBC∴△ABC≌()用上面的规律可以判断两个三角形.判断,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.又如图,在△ABC与△ABD中AB=。 CA=。=BD∴△ABC≌△ABD()三、应用新知巩固练习:填空例1:如上图在四边形ACBD中,AC=AD,BD=BC,则∠C=∠D,请说明理由解:在△ABC与△ABD中AB=。 CA=。=BD∴△ABC≌△ABD()∴∠C=∠D()C'B'A'CBA个人收集整理仅供参考学习2、如下图2,AB=AC,BD=DC3、如下图3,AM=AN,BM=BN求证:△ABD≌△ACD求证:△AMB≌△ANB证明:在△ABD和△ACD中证明:在△AMB和△ANB中AB=AC(已知)AM=()=(已知)=BN(已知)AD=AD(公共边)=(公共边)∴△ABD△ACD()∴≌()5、如下图5,PA=PB,PC是△PAB的中线,∠A=55°,求:∠B的度数解: PC是AB边上的中线,∴AC=(中线的定义)在中≌()∴∠A=∠B() ∠A=55°(已知)∴∠B=∠A=55°(等量代换)6、如右图,AB=CD,BF=DE。AE=CF。证明:△ABF与△CDE全等。小组内交流书写的格式和步骤。小结:证明三角形全等的格式与步骤:四、自我检测(课后拓展):1、如图,ΔABC中,AB=AC,BE=EC,则由“SSS”可判定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()A、ΔABD≌ΔACDB、ΔABE≌ΔACEC、ΔBED≌ΔCEDD、以上答案都不对2、如图,已知AB=CD,AD=BC,则≌4、如图,AB=DC,BF=CE,AE=DF,你能找到一对全等的三角形吗?说明你的理由.EDABCCDABEF个人收集整理仅供参考学习5、如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF你能找到哪两个三角形全...