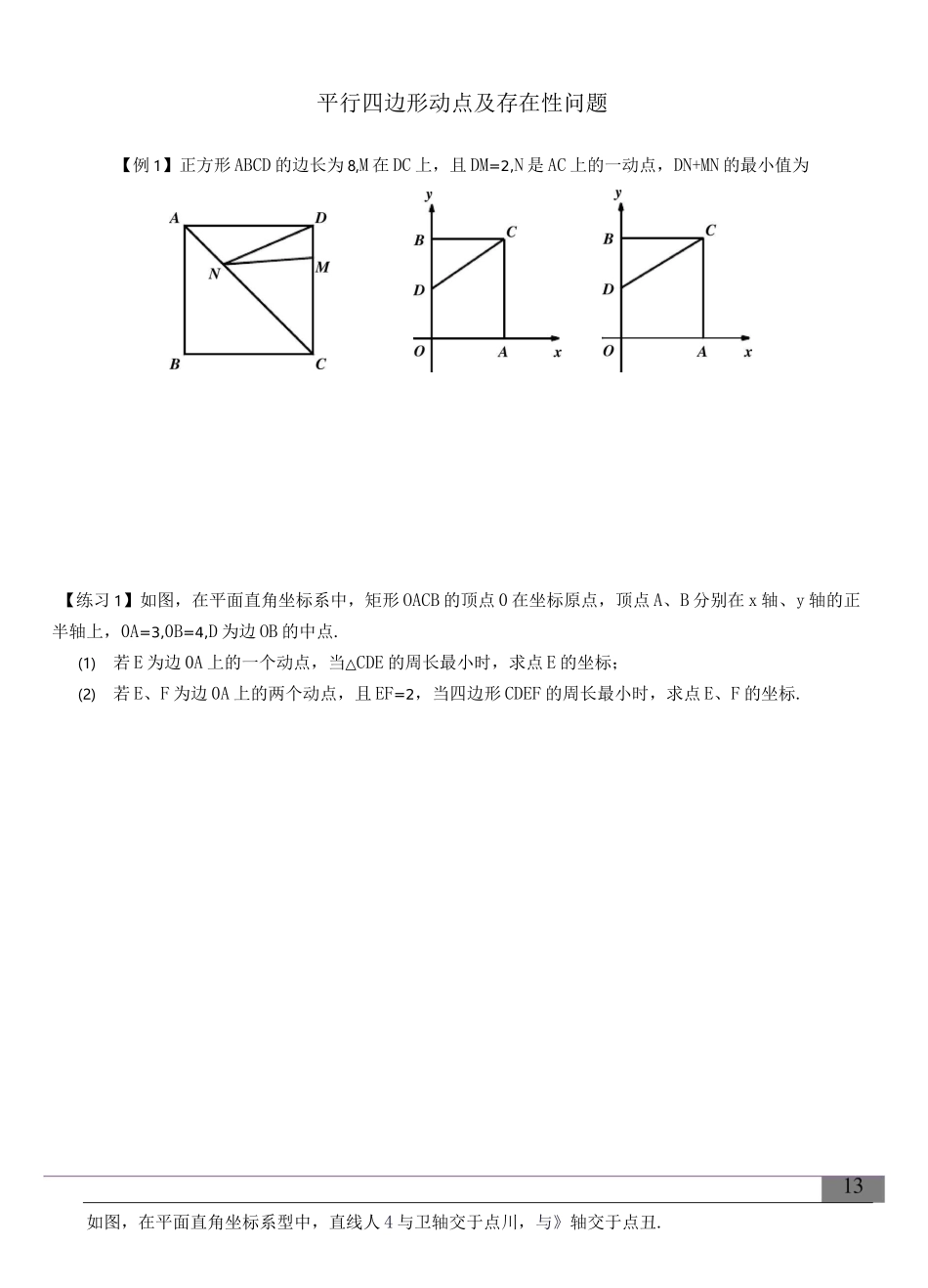
平行四边形动点及存在性问题【例1】正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为【练习1】如图,在平面直角坐标系中,矩形OACB的顶点0在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,0A=3,0B=4,D为边OB的中点.(1)若E为边0A上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边0A上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.如图,在平面直角坐标系型中,直线人4与卫轴交于点川,与》轴交于点丑.⑴求点4占的坐标.(2)若戸是直线x=-2±的一动点,则在坐标平面内是否存在点?使得以儿E玖Q为顶点的四边形是菱形?若存在,求岀点Q的坐标,若不存在,请说明理由.【例3】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当三角形△ODP是腰长为5的等腰三角形时,P的坐标为;A*B13【练习2】如图,在平面直角坐标系中,AB〃OC,A(0,12),B(a,c),C(b,0),并且a,b满足b二ja^21+J2T二a+16•一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点0出发在线段0C上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、0同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒)(1)求B、C两点的坐标;(2)当t为何值时,四边形PQCB是平行四边形?并求出此时P、Q两点的坐标;(3)当t为何值时,APQC是以PQ为腰的等腰三角形?并求出P、Q两点的坐标.【例4】(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,0为坐标原点,点E的坐标为(4,3),则点M的坐标为;(2)在直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.13【练习3】如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).(1)求G点坐标;(2)求直线EF解析式;(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.【例5】在RtAABC中,ZB=90°,AC=60cm,ZA=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(00)(1)_________________________点E的坐标为,F的坐标为(2)当t为何值时,四边形POFE是平行四边形;(3)是否存在某一时刻,使APEF为直角三角形?若存在,一个角度得到△FEC,EF的中点为G,连接DG,在旋转过程中,DG的最大值是;最小值是.3、已知AABC是等腰直角三角形,ZBAC=90°,点D是BC的中点.作正方形DEFG,连接AE,BG,若BC二DE=4,将正方形DEFG绕点D旋转,当AE取最小值时,AF=.4、在三角形纸片ABC中,已知ZABC=90°,AB=6,BC=8。过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为____.BD135、如图,在梯形ABCD中,AD〃BC,ZB=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm...