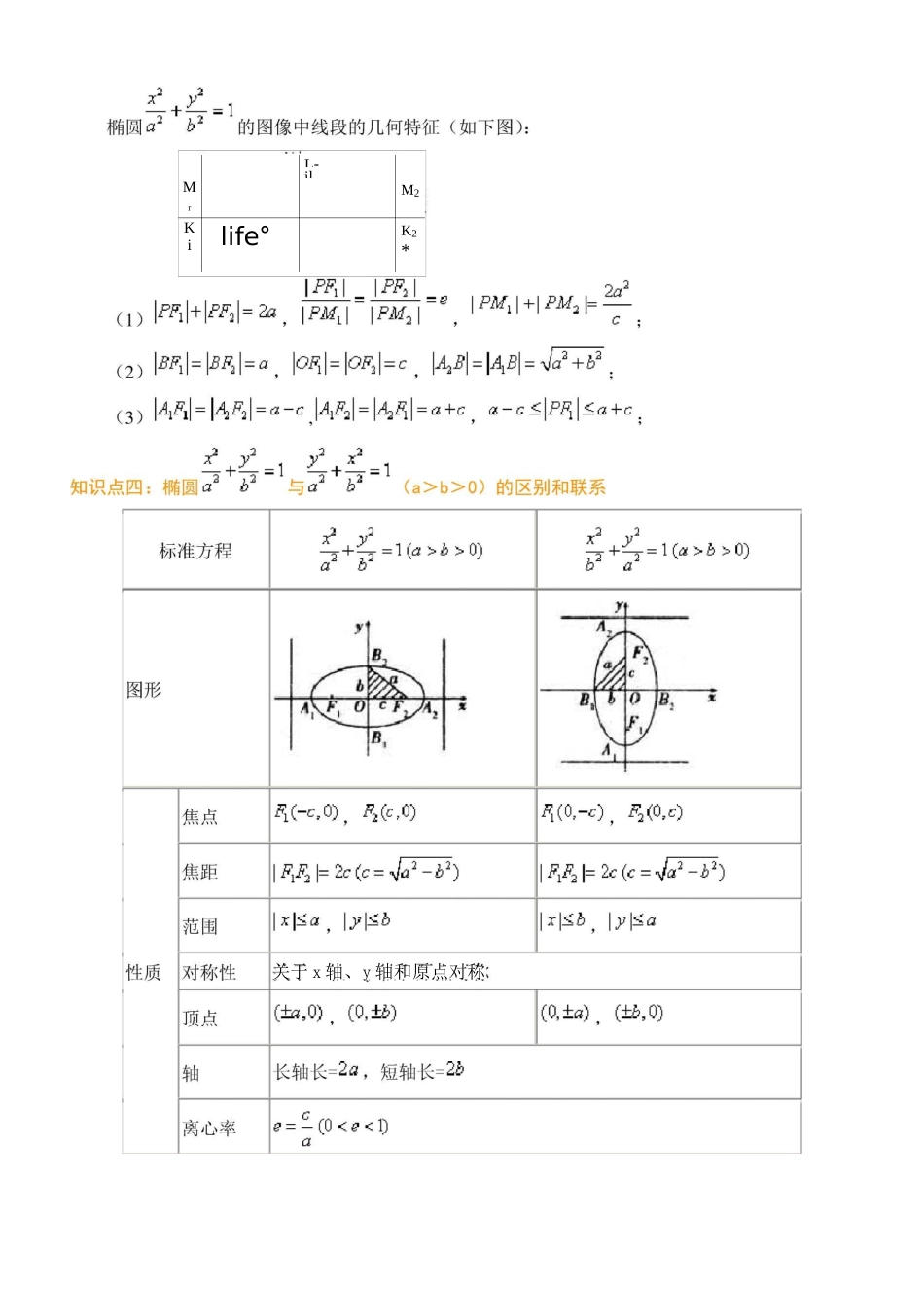
教学课椭知识点一:椭圆的定平面内一个动点尸到两个定点吗、),这个点尸的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦注意:若冋1+肉二阳I,则动点尸的轨迹为线段恥;若KI+KIb>0)与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为A(—a,0),A2(a,0),B1(0,—b),B2(0,b)。③线段A]A2,B1B2分别叫做椭圆的长轴和短轴,lA]A2l=2a,lB]B2l=2b。a和b分别叫做椭圆的长半轴长和短半轴长。(4)离心率2cc3———=—①椭圆的焦距与长轴长度的比叫做椭圆的离心率,用e表示,记作②因为a>c>0,所以e的取值范围是0VeVl°e越接近1,则c就越接近a,从而b=越小,因此椭圆越扁;反之,e越接近于0,c就越接近0,从而b越接近于a,这时椭圆就越接近于圆。当且仅当a=b时,c=0,这时两个焦点重合,图形变为圆,方程为x2+y2=a2。L-il...MrM2Kilife°K2*关于x轴、y轴和原点对称s=—(0<<1)都有a>b>0和注意:椭圆同。题型椭圆焦点三角形面积公式的应配方得:(r+r)2一2rr-2rrcos0=4c2.121212即4a2一2rr(1+cos0)=4c2.122(a2一c2)2b21+cos01+cos0由任意三角形的面积公式S=—rrsin0=b2—sin°亠=b2•AF1PF22121+CO2•002sinco22—b2•0—b22cos2-AF!PF2典题妙例1若P是椭圆_0_+64二1上的一点,仆F2是其焦点,且ZFPF二60°,求122222r十N"彳十計1(a>b>0)的相同点为形状、大小都相同,参数间的关系a2二b2+c2;不同点为两种椭圆的位置不同,它们的焦点坐标也不相0,准线方程焦半径IPF\\=aIPF2\^d—QX参考答积是^3,准线方程为x=±竿,求椭圆的标准方程.的=—-,△FPF212PF-PF6.已知椭圆的中心在原点,F、F为左右焦点,P为椭圆上一点,且112IPFI-1PFIgS=b2tan=9tan30°=3、3.AF!PF22故选答案A.练习1=1,解:设ZFPF=0,则cos0=—12IPFI-1PFI212PF-PF12DC.v'3F1"2的面积为(若IPFI-1PFIPF-PF12F2分别是椭圆的左、右焦点,X2y2例2已知P是椭圆25+专=1上的点,F、两个解法的优劣立解法一复杂繁冗,运算量大,解法二简捷明解法256v'364抒=—rrsin0212SAF!=256r2+r2一曲F1PF2中,由余弦定理得:二2a.由椭圆的第一定义得:〔+r2△F1"2的面积-解法一:在椭圆-00+64=1中,a=10,b=&c=6,而0=60°•记IPF1=r_,IPF_I=r_.100640点P在椭圆上,配方,得:(r+r)2—3rr=144.1212...400—3rr=144.从而12在椭圆100+64二1中,b2二64,而0=60°.S=b2tan=64tan30°=3AF1PF223a=\;b2+c2—2,c=<3或c=c2+b2c2+11==c+=又®鼻=去3,即c3c2b=1.PF-PF.12-F-PF1设ZFPF=9,cos0==一一,9=120。.12IPFI-1PFI21=b2tan=b2tan60°=>,3b2=、3,SAF!PF26.一x2-这时椭圆的标准方程为才+y2=】;