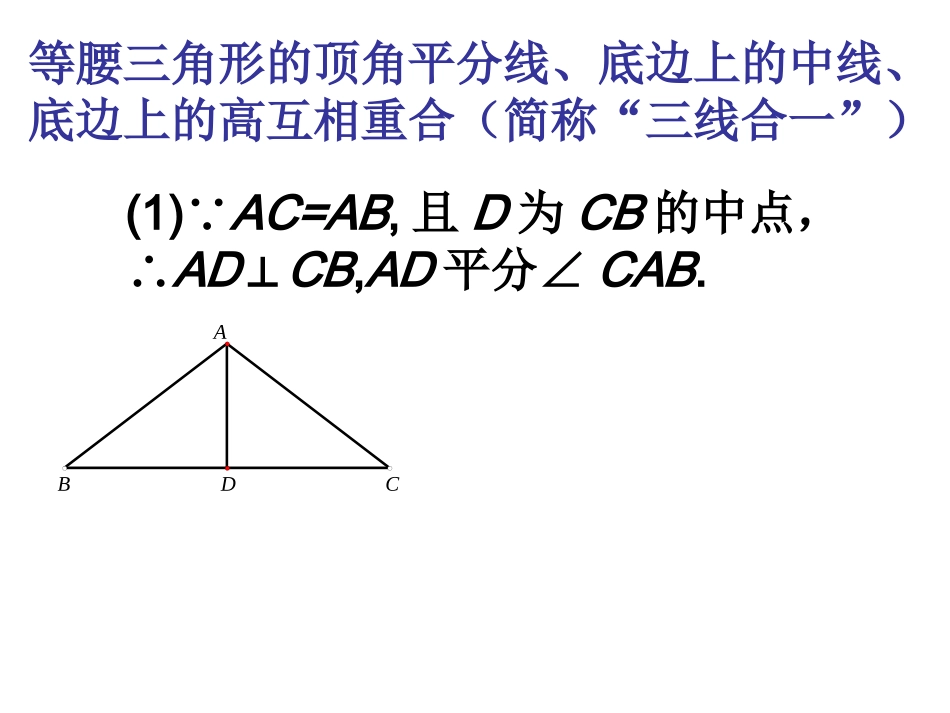
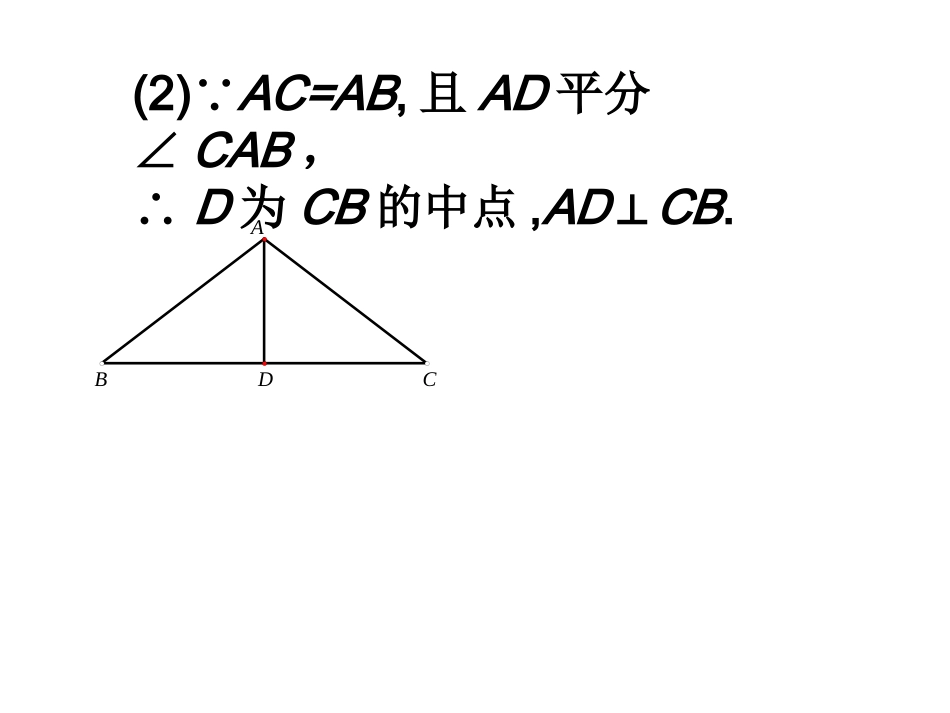
等腰三角形的三线合一复习课等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“三线合一”)(1)∵AC=AB,且D为CB的中点,∴AD⊥CB,AD平分∠CAB.CDAB(2)∵AC=AB,且AD平分∠CAB,∴D为CB的中点,AD⊥CB.CDAB(3)∵AC=AB,且AD⊥CB,∴D为CB的中点,AD平分∠CAB.CDAB例1.已知AB′=AB,E为BB′的中点,EC⊥AB′,ED⊥AB.求证:CE=EDCDB'EAB例2.已知:AB′=AB,BC⊥AB′.求证:∠1=0.5BAB∠′.1CB'AB例3.已知:如图,在△ABC中,AB=AC,E在AC上,D在BA的延长线上,AD=AE,连接DE.求证:DE⊥BC.DABCE例3.已知:如图,在△ABC中,AB=AC,E在AC上,D在BA的延长线上,AD=AE,连接DE.求证:DE⊥BC.图中AR这条线段的引出可以看成是:1.过A点作DE的平行线.2.过A点作BC的垂线.3.∠BAC的角平分线.4.BC边的中线.DABCE还有以下的招法1.过A点作BC的平行线.2.过B点作AC的平行线,交DE的延长线于G点.3.过C点作AB的平行线,交DE的延长线于N点4.过B点作DE的平行线,交CA的延长线于Q点.5.过D点作DOBC∥交CA的延长线于O点,并延长DE交BC于F点.6.过C点作DE的平行线,交BA的延长线于R点7.过D点作AC的平行线,交BC的延长线于H点,并延长DE交BC于F点.拓展提高:课本背后的性质已知:AB=AC,DE⊥AB,DF⊥AC,求证:DE+DF是一个定值.FEDCBA