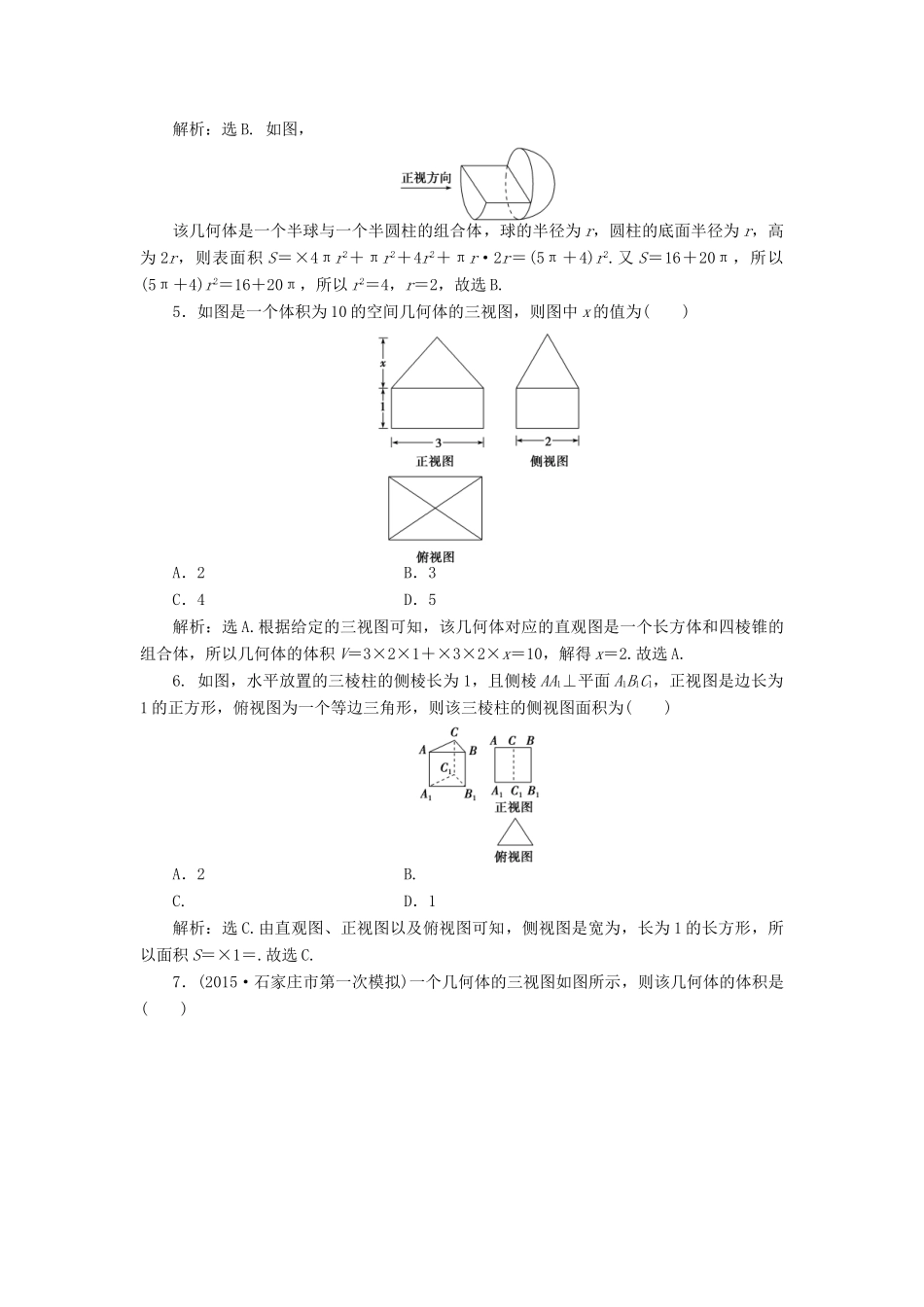
第一部分专题四立体几何第1讲空间几何体专题强化精练提能理[A卷]1.如图所示是一个物体的三视图,则此三视图所描述物体的直观图是()解析:选D.先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确,故选D.2.如图是正方体截去阴影部分所得的几何体,则该几何体的侧视图是()解析:选C.此几何体的侧视图是从左边往右看,故其侧视图应为C.3.(2014·高考陕西卷)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是()A.4πB.3πC.2πD.π解析:选C.由几何体的形成过程知所得几何体为圆柱,底面半径为1,高为1,其侧面积S=2πrh=2π×1×1=2π.4.(2015·高考全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.8解析:选B.如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,所以(5π+4)r2=16+20π,所以r2=4,r=2,故选B.5.如图是一个体积为10的空间几何体的三视图,则图中x的值为()A.2B.3C.4D.5解析:选A.根据给定的三视图可知,该几何体对应的直观图是一个长方体和四棱锥的组合体,所以几何体的体积V=3×2×1+×3×2×x=10,解得x=2.故选A.6.如图,水平放置的三棱柱的侧棱长为1,且侧棱AA1⊥平面A1B1C1,正视图是边长为1的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图面积为()A.2B.C.D.1解析:选C.由直观图、正视图以及俯视图可知,侧视图是宽为,长为1的长方形,所以面积S=×1=.故选C.7.(2015·石家庄市第一次模拟)一个几何体的三视图如图所示,则该几何体的体积是()A.64B.72C.80D.112解析:选B.由三视图可知该几何体是一个组合体,下面是一个棱长为4的正方体;上面是一个三棱锥,三棱锥的高为3.故所求体积为43+××4×4×3=72.8.正三棱柱ABCA1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥AB1DC1的体积为()A.3B.C.1D.解析:选C.由题意可知AD⊥BC,由面面垂直的性质定理可得AD⊥平面DB1C1,又AD=2sin60°=,所以VAB1DC1=AD·S△B1DC1=×××2×=1,故选C.9.(2015·日照二模)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥侧面积和体积分别是()A.4,8B.4,C.4(+1),D.8,8解析:选B.由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为=,所以S侧=4×=4,V=×22×2=.10.(2015·济南市第一次模拟)如图,在正四棱柱ABCDA1B1C1D1中,点P是平面A1B1C1D1内一点,则三棱锥PBCD的正视图与侧视图的面积之比为()A.1∶1B.2∶1C.2∶3D.3∶2解析:选A.根据题意,三棱锥PBCD的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,故三棱锥PBCD的正视图与侧视图的面积之比为1∶1.11.已知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是________(把正确的图的序号都填上).解析:几何体由四棱锥与四棱柱组成时,得①正确;几何体由四棱锥与圆柱组成时,得②正确;几何体由圆锥与圆柱组成时,得③正确;几何体由圆锥与四棱柱组成时,得④正确.答案:①②③④12.(2015·滨州模拟)一平面截一球得到直径为2cm的圆面,球心到这个平面的距离是2cm,则该球的体积是________.解析:因为球心和截面圆心的连线垂直于截面,由勾股定理得,球半径R==3,故球的体积为πR3=36π(cm3).答案:36πcm313.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长是10cm,则圆锥的母线长为________cm.解析:作出圆锥的轴截面如图,设SA=y,O′A′=x,利用平行线截线段成比例,得SA′∶SA=O′A′∶OA,则(y-10)∶y=x∶4x,解得y=.所以圆锥的母线长为cm.答案:14.如图是某空间几何体的三视图,则该几何体的体积为________.解析:由三视图可知,该几何体是棱长为2,2,...