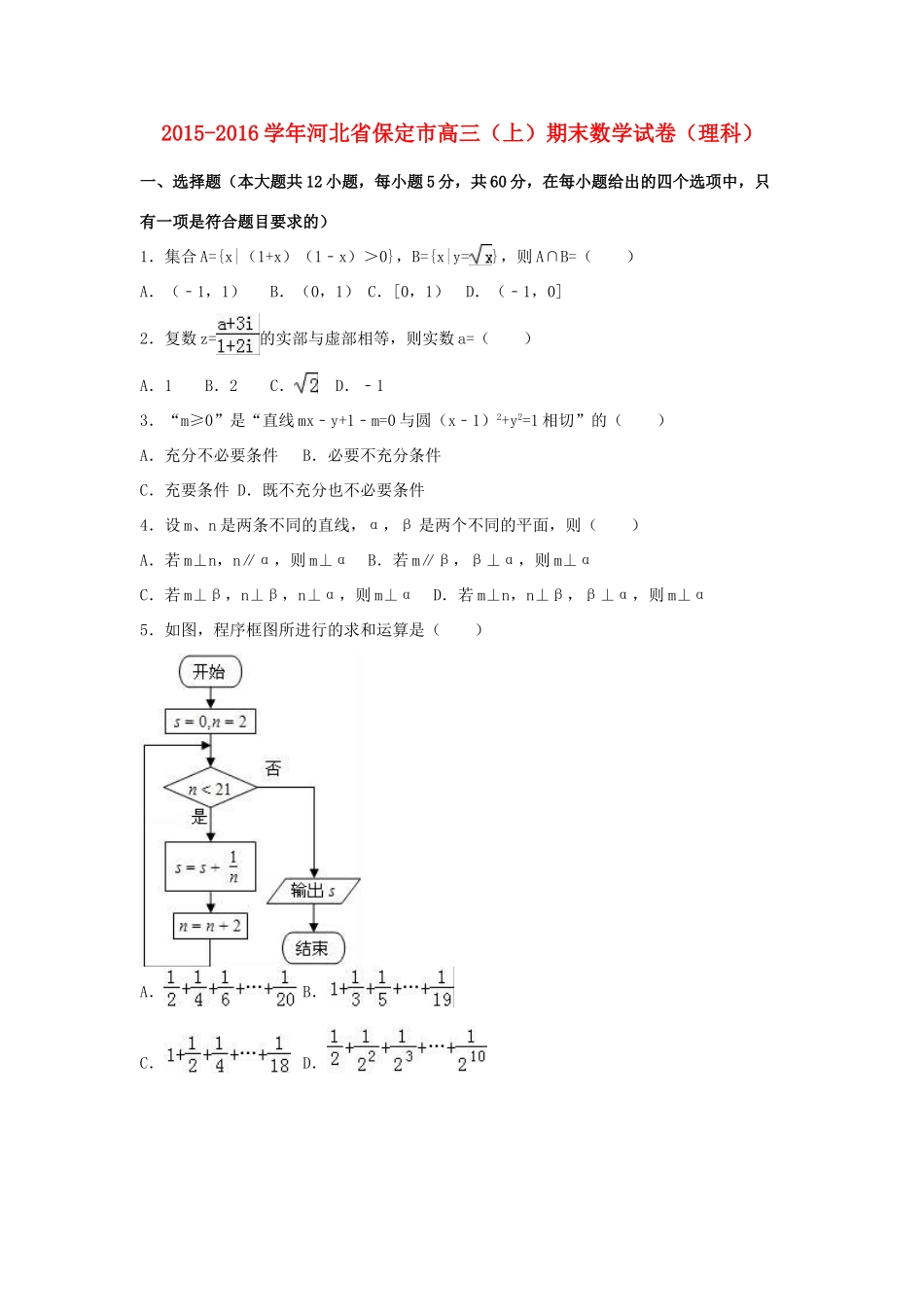
2015-2016学年河北省保定市高三(上)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={x|(1+x)(1﹣x)>0},B={x|y=},则A∩B=()A.(﹣1,1)B.(0,1)C.[0,1)D.(﹣1,0]2.复数z=的实部与虚部相等,则实数a=()A.1B.2C.D.﹣13.“m≥0”是“直线mx﹣y+1﹣m=0与圆(x﹣1)2+y2=1相切”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设m、n是两条不同的直线,α,β是两个不同的平面,则()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.如图,程序框图所进行的求和运算是()A.B.C.D.6.将函数f(x)=sin(4x+)图象上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是直线()A.x=B.x=C.x=D.x=7.下列四个判断:①某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学的平均分为;②10名工人某天生产同一种零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;③设从总体中抽取的样本为(x1,y1),(x2,y2),…,(xn,yn),若记=xi,=yi,则回归直线方程=bx+a必过点(,);④已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤0)=0.4,则P(ξ>2)=0.2.其中正确判断的个数有()A.0个B.1个C.2个D.3个8.已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线x2﹣ay2=a的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a等于()A.B.C.D.9.等差数列{an}中,a1=2016,前n项和为Sn,若﹣=﹣2,则S2016=()A.2014B.2015C.2016D.201710.已知++=,且与的夹角为,||=||,设,的夹角为θ,则tanθ=()A.B.C.﹣1D.﹣11.已知a>0且a≠1,函数f(x)=+3loga(﹣≤x≤),设函数f(x)的最大值是A,最小值是B,则()A.A﹣B=4B.A+B=4C.A﹣B=6D.A+B=612.函数f(x)=﹣k在(0,+∞)上有两个不同的零点a,b(a<b),则下面结论正确的是()A.sina=acosbB.sinb=﹣bsinaC.cosa=bsinbD.sina=﹣acosb二、填空题:本大题共4小题,每小题5分.13.一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用_______个这样的几何体可以拼成一个棱长为2的正方体.14.若a=cosxdx,则(++)4的展开式中常数项为_______.15.设函数,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x﹣2y在D上的最大值为_______.16.已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若同时满足条件:①∀x∈R,f(x)<0或g(x)<0;②∃x∈(﹣∞,﹣4),f(x)g(x)<0.则m的取值范围是_______.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.在△ABC中,内角A,B,C所对的边长分别为a,b,c,若向量=(sinA,sinB),=(cosB,cosA),•=+cos(A+B).(1)求∠C;(2)若c=3,b=a,求△ABC的面积S.18.已知数列{an},{bn},其中a1=1,an=+,=﹣(n∈N*).(1)求证:数列{bn﹣}是等比数列;(2)求数列{bn}的通项公式及数列{anbn}的前n项和Sn.19.某校为了在竞争中更好的发展,校领导专门聘请省内外专家组成“学校建设和发展”专家顾问委员会,项专家接脑、帮助学校制定未来五年发展规划,并召开了座谈会,问需于民,问计与民,广泛征询专家,普通老师和同学们对学校发展的意见和建议,此次座谈会共邀请了50名代表参加,他们分别是专家20人,普通教师15人,学生15人,现从50名代表中随机选出3名做典型发言.(1)求选出的3名代表中,专家比普通教师多一人的概率;(2)若记选出的3名代表中专家的人数为ξ,求ξ的分布列和数学期望.20.在三棱锥P﹣ABC中,AB⊥BC,平面PAB⊥平面ABC,BC=2AB=1,PC=,∠PBA=.(1)求证:BC⊥PB;(2)求二面角A﹣PC﹣B的大小.21.已知抛物线C1:y...