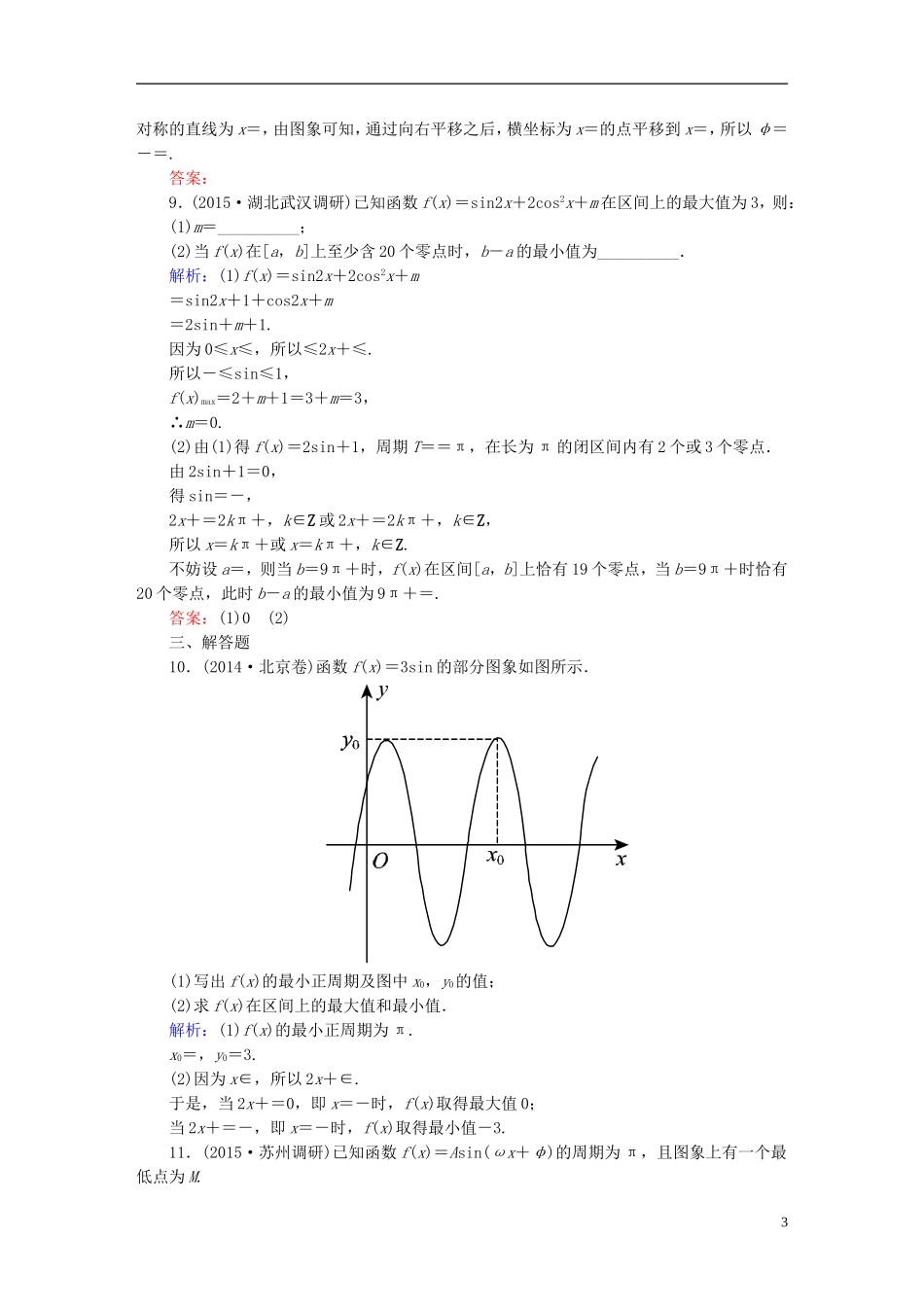
课时作业18函数y=Asin(ωx+φ)的图象及简单三角函数模型的应用一、选择题1.(2014·湖州二模)将函数y=sin2x+cos2x的图象向左平移个单位长度,所得图象对应的函数解析式可以是()A.y=cos2x+sin2xB.y=cos2x-sin2xC.y=sin2x-cos2xD.y=sinxcosx解析:y=sin2x+cos2x=sin――→y=sin=sin=cos=cos2x-sin2x.答案:B2.(2014·福建卷)将函数y=sinx的图象向左平移个单位,得到函数y=f(x)的图象,则下列说法正确的是()A.y=f(x)是奇函数B.y=f(x)的周期为πC.y=f(x)的图象关于直线x=对称D.y=f(x)的图象关于点对称解析:函数y=sinx的图象向左平移个单位后,得到函数f(x)=sin=cosx的图象,f(x)=cosx为偶函数,排除A;f(x)=cosx的周期为2π,排除B;因为f=cos=0,所以f(x)=cosx不关于直线x=对称,排除C;故选D.答案:D3.(2014·新课标全国卷Ⅰ)在函数①y=cos|2x|,②y=|cosx|,③y=cos,④y=tan中,最小正周期为π的所有函数为()A.①②③B.①③④C.②④D.①③解析:①y=cos|2x|,最小正周期为π;②y=|cosx|,最小正周期为π;③y=cos,最小正周期为π;④y=tan,最小正周期为,所以最小正周期为π的所有函数为①②③,故选A.答案:A4.(2014·山东青岛一模)函数f(x)=Asin(ωx+φ)的部分图象如图所示,为了得到y=sin2x的图象,只需将f(x)的图象()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度解析:观察图象可知,A=1,T=π,1∴ω=2,f(x)=sin(2x+φ).将代入上式得sin=0.由已知得φ=,故f(x)=sin.由f(x)=sin2知,为了得到y=sin2x的图象,只需将f(x)的图象向右平移个单位长度.故选B.答案:B5.(2014·天津卷)已知函数f(x)=sinωx+cosωx(ω>0),x∈R.在曲线y=f(x)与直线y=1的交点中,若相邻交点距离的最小值为,则f(x)的最小正周期为()A.B.C.πD.2π解析:由题意得函数f(x)=2sin(ω>0),又曲线y=f(x)与直线y=1相邻交点距离的最小值是,由正弦函数的图象知,ωx+=和ωx+=对应的x的值相差,即=,解得ω=2,所以f(x)的最小正周期是T==π.答案:C6.(2014·长春模拟)函数f(x)=sin(2x+φ)向左平移个单位后是奇函数,则函数f(x)在上的最小值为()A.-B.-C.D.解析:函数f(x)=sin(2x+φ)向左平移个单位后得到函数为f=sin=sin,因为此时函数为奇函数,所以+φ=kπ(k∈Z),所以φ=-+kπ(k∈Z).因为|φ|<,所以当k=0时,φ=-,所以f(x)=sin.当0≤x≤时,-≤2x-≤,即当2x-=-时,函数f(x)=sin有最小值为sin=-.答案:A二、填空题7.(2014·陕西五校三模)函数y=sinx(3sinx+4cosx)(x∈R)的最大值为M,最小正周期为T,则有序数对(M,T)为__________.解析:因为y=sinx(3sinx+4cosx)=+2sin2x=2sin2x-cos2x+≤+=4,所以M=4,T=π,所以有序数对(M,T)为(4,π).答案:(4,π)8.已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=__________.解析:函数f(x)=sin2x的图象在y轴右侧的第一个对称轴为2x=,所以x=,关于x=2对称的直线为x=,由图象可知,通过向右平移之后,横坐标为x=的点平移到x=,所以φ=-=.答案:9.(2015·湖北武汉调研)已知函数f(x)=sin2x+2cos2x+m在区间上的最大值为3,则:(1)m=__________;(2)当f(x)在[a,b]上至少含20个零点时,b-a的最小值为__________.解析:(1)f(x)=sin2x+2cos2x+m=sin2x+1+cos2x+m=2sin+m+1.因为0≤x≤,所以≤2x+≤.所以-≤sin≤1,f(x)max=2+m+1=3+m=3,∴m=0.(2)由(1)得f(x)=2sin+1,周期T==π,在长为π的闭区间内有2个或3个零点.由2sin+1=0,得sin=-,2x+=2kπ+,k∈Z或2x+=2kπ+,k∈Z,所以x=kπ+或x=kπ+,k∈Z.不妨设a=,则当b=9π+时,f(x)在区间[a,b]上恰有19个零点,当b=9π+时恰有20个零点,此时b-a的最小值为9π+=.答案:(1)0(2)三、解答题10.(2014·北京卷)函数f(x)=3sin的部分图象如图所示.(1)写出f(x)的最小正周期及图中x0,y0的值;(2)...