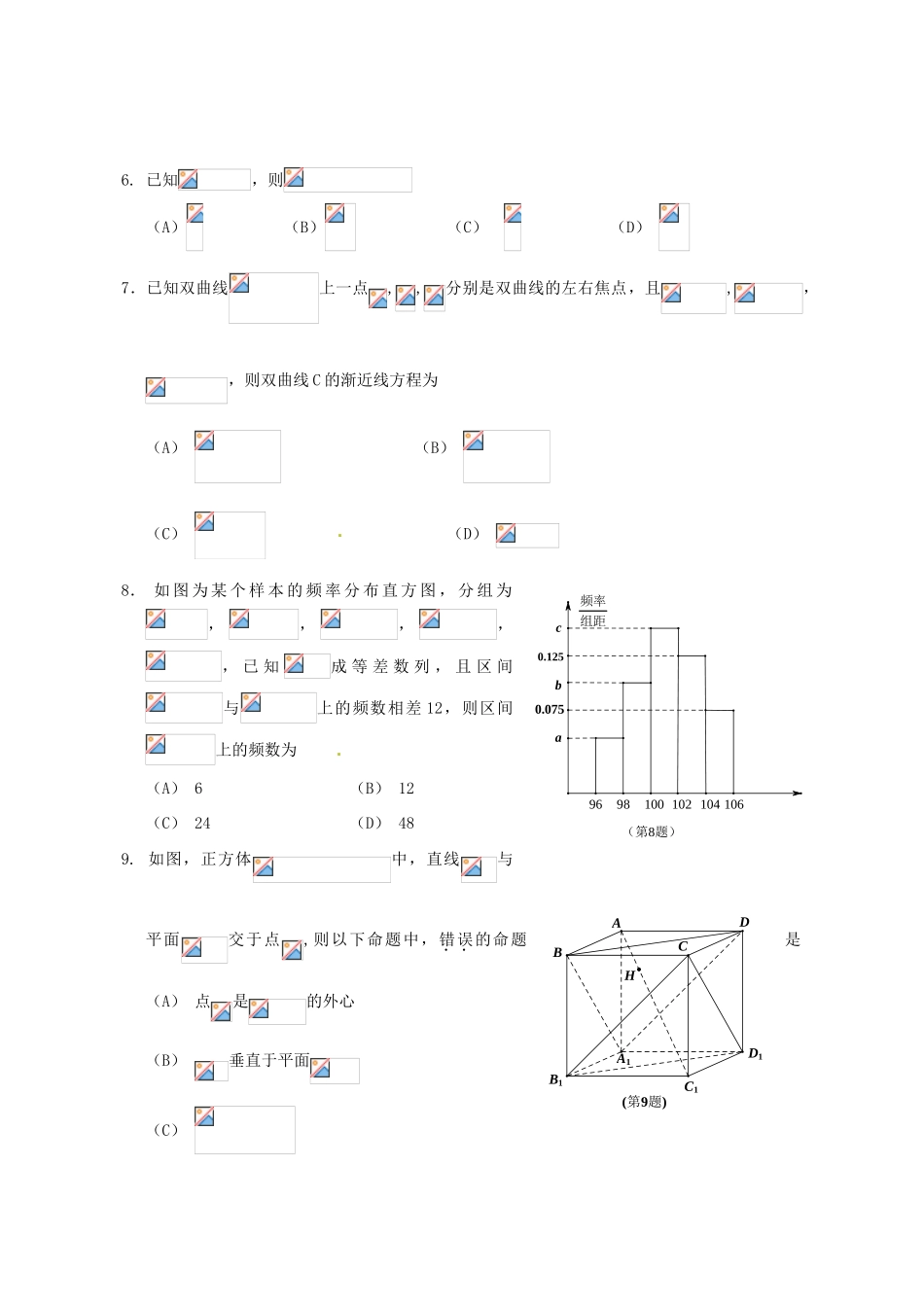
否(第5题)是输出mm=m+2nm≥8?输入m,n结束开始高2013级高考适应性测试(B卷)数学(文史类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至4页.考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效.满分150分,考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题,共50分)注意事项:必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.一、选择题:本大题共10个小题,每小题5分,共50分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,,,则(A)(B)(C)(D)2.“”是“”的(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件3.设是纯虚数,其中是虚数单位,则(A)(B)(C)(D)4.若四面体的三视图如右图所示,则该四面体的体积为(A)8(B)12(第4题图)(C)16(D)245.执行如右图所示的程序框图,如果输入,则输出的的值为(A)8(B)9(C)10(D)116.已知,则(A)(B)(C)(D)7.已知双曲线上一点,,分别是双曲线的左右焦点,且,,,则双曲线C的渐近线方程为(A)(B)(C)(D)8.如图为某个样本的频率分布直方图,分组为,,,,,已知成等差数列,且区间与上的频数相差12,则区间上的频数为(A)6(B)12(C)24(D)489.如图,正方体中,直线与平面交于点,则以下命题中,错误的命题是(A)点是的外心(B)垂直于平面(C)(第8题)频率组距0.075b0.125ca9698100102104106(第9题)DAD1A1CBB1C1H(D)直线和所成角为45°10.已知函数的最大值与最小值的关系是(A)(B)(C)(D)第Ⅱ卷(非选择题,共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.试题卷上作答无效.二、填空题:本大题共5小题,每小题5分,共25分.11.计算:=.12.已知平面向量,,且,则.13.右图是抛物线形拱桥,当水面在时,拱顶离水面2米,水面宽4米,水面下降0.42米后,水面宽为米.(第13题图)14.设不等式组所确定的平面区域为D,在圆+=4上任取一点P,则点P落在区域D内的概率为_______.15.已知有限集.如果A中元素满足,就称A为“创新集”,给出下列结论:①集合是“创新集”;②若集合是“创新集”,则;③是“创新集”,则;④不可能是“创新集”.其中正确的结论是___________.(填上你认为所有正确的结论序号)三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.不能答试卷上,请答在答题卡相应的方框内.16.(本小题满分12分)设等差数列的前项和为,且,.()求数列的通项公式;(Ⅱ)求使得成立的的所有取值.17.(本小题满分12分)某体训队共有六位同学,他们的身高(单位:米)以及体考成绩(单位:分)如下表所示:身高1.661.681.721.761.781.83成绩798086818884(Ⅰ)求该体训队同学体考成绩的中位数与平均数.(Ⅱ)从该体训队中任选2人,求选到的2人的身高都在1.70米以上且成绩都在[82,90)中的概率.18.(本小题满分12分)已知函数()求函数的单调递增区间;(II)将函数的图像各点纵坐标不变,横坐标伸长为原来的2倍,然后向左平移个单位,得函数的图像.若分别是三个内角的对边,当时,取得最大值,又,求的面积.19.(本小题满分12分)已知梯形中,,DCBACBADFEGEF,,、分别是、上的点,且,设,是的中点.沿将梯形翻折,使平面平面(如图).()当时,求证:;(II)若以、、、为顶点的三棱锥的体积记为,求的表达式及其最大值.20.(本小题满分13分)已知椭圆:的离心率为,是椭圆的两个焦点,是椭圆上任意一点,且的周长是.()求椭圆的方程;(Ⅱ)设圆:,过椭圆的上顶点作圆的两条切线交椭圆于、两点,求直线的斜率.21.(本小题满分14分)已知函数.(I)讨论的单调性;(II)若存在正实数,使得,求的最大值;(III)若且时,不等式恒成立,求实数的取值范围.MExOyF高2013级高考适应性测试(B卷)数学(文史类)参考答案说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评...