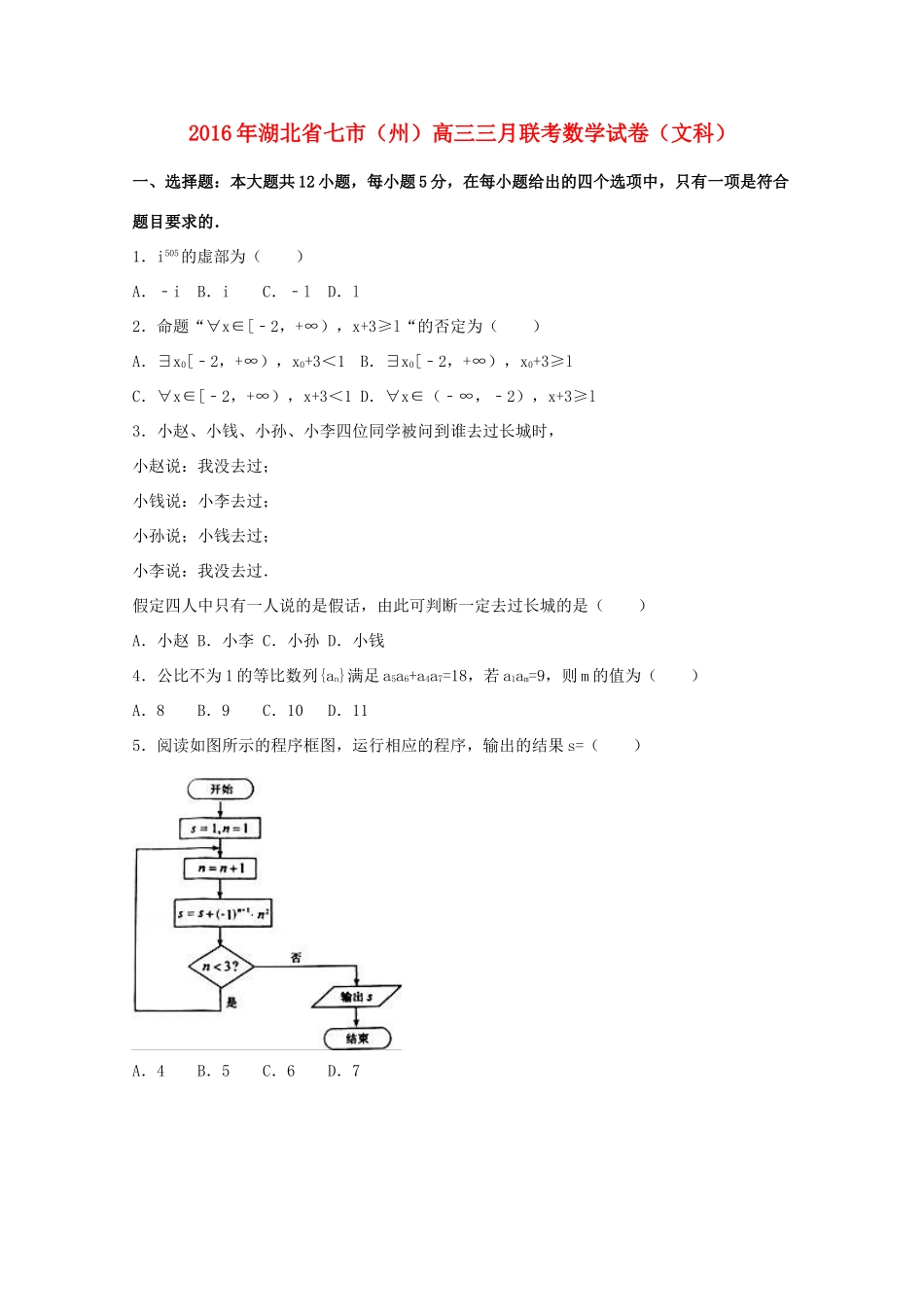
2016年湖北省七市(州)高三三月联考数学试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.i505的虚部为()A.﹣iB.iC.﹣lD.l2.命题“∀x∈[﹣2,+∞),x+3≥l“的否定为()A.∃x0[﹣2,+∞),x0+3<1B.∃x0[﹣2,+∞),x0+3≥lC.∀x∈[﹣2,+∞),x+3<1D.∀x∈(﹣∞,﹣2),x+3≥l3.小赵、小钱、小孙、小李四位同学被问到谁去过长城时,小赵说:我没去过;小钱说:小李去过;小孙说;小钱去过;小李说:我没去过.假定四人中只有一人说的是假话,由此可判断一定去过长城的是()A.小赵B.小李C.小孙D.小钱4.公比不为1的等比数列{an}满足a5a6+a4a7=18,若a1am=9,则m的值为()A.8B.9C.10D.115.阅读如图所示的程序框图,运行相应的程序,输出的结果s=()A.4B.5C.6D.76.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3寸,容纳米2000斛(1丈=10尺,l尺=10寸,斛为容积单位,l斛≈1.62立方尺,π≈3),则圆柱底圆周长约为()A.l丈3尺B.5丈4尺C.9丈2尺D.48丈6尺7.己知直线ax+by﹣6=0(a>0,b>0)被圆x2+y2﹣2x﹣4y=0截得的弦长为2,则ab的最大值是()A.9B.C.4D.8.T为常数,定义fT(x)=,若f(x)=x﹣lnx,则f3[f2(e)]的值为.()A.e﹣lB.eC.3D.e+l9.设M,N是抛物线C:y2=2px(p>0)上任意两点,点E的坐标为(﹣λ,0)(λ≥0),若•的最小值为0,则λ=()A.0B.C.pD.2p10.已知某几何体的三视图如图所示,其中俯视图是正三角形,则该几何体的体积为()A.B.2C.3D.411.已知集合P={n|n=2k﹣1,k∈N+,k≤50},Q={2,3,5},则集合T={xy|x∈P,y∈Q}中元素的个数为()A.147B.140C.130D.11712.设向量=(1,k),=(x,y),记与的夹角为θ.若对所有满足不等式|x﹣2|≤y≤1的x,y,都有θ∈(0,),则实数k的取值范围是()A.(﹣1,+∞)B.(﹣1,0)∪(0,+∞)C.(1,+∞)D.(﹣1,0)∪(1,+∞)二、填空题:本大题共4小题,每小题5分.13.观察下列等式l+2+3+…+n=n(n+l);l+3+6+…+n(n+1)=n(n+1)(n+2);1+4+10+…n(n+1)(n+2)=n(n+1)(n+2)(n+3);可以推测,1+5+15+…+n(n+1)(n+2)(n+3)=.14.函数f(x)=3﹣x+x2﹣4的零点个数是.15.如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=m.16.平面区域A={(x,y)|x2+y2<4,x,y∈R},B={(x,y)||x|+|y|≤3,x,y∈R).在A内随机取一点,则该点取自B的概率为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知函数f(x)=sinx+cosx(x∈R).(Ⅰ)若a∈[0,π]且f(a)=2,求a;(Ⅱ)先将y=f(x)的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x=对称,求θ的最小值.18.某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7),[0.7,0.8),[0.8,0.9],购物金额的频率分布直方图如下:电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:购物金额分组[0.3,0[0.5,0[0.6,0[0.8,0.5).6).8).9]发放金额50100150200(I)求这1000名购物者获得优惠券金额的平均数;(Ⅱ)以这1000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.19.如图,一个侧棱长为l的直三棱柱ABC﹣A1B1C1容器中盛有液体(不计容器厚度).若液面恰好分别过棱AC,BC,B1C1,A1Cl的中点D,E,F,G.(I)求证:平面DEFG∥平面ABB1A1;(Ⅱ)当底面ABC水平放置时,求液面的高.20.已知圆心为H的圆x2+y2+2x﹣15=0和定点A(1,0),B是圆上任意一点,线段AB的中垂线l和直线BH相交于点M,当点B在圆上运动...