招生全国统一考试数学理试题（天津卷，含解析）-人教版高三全册数学试题VIP免费

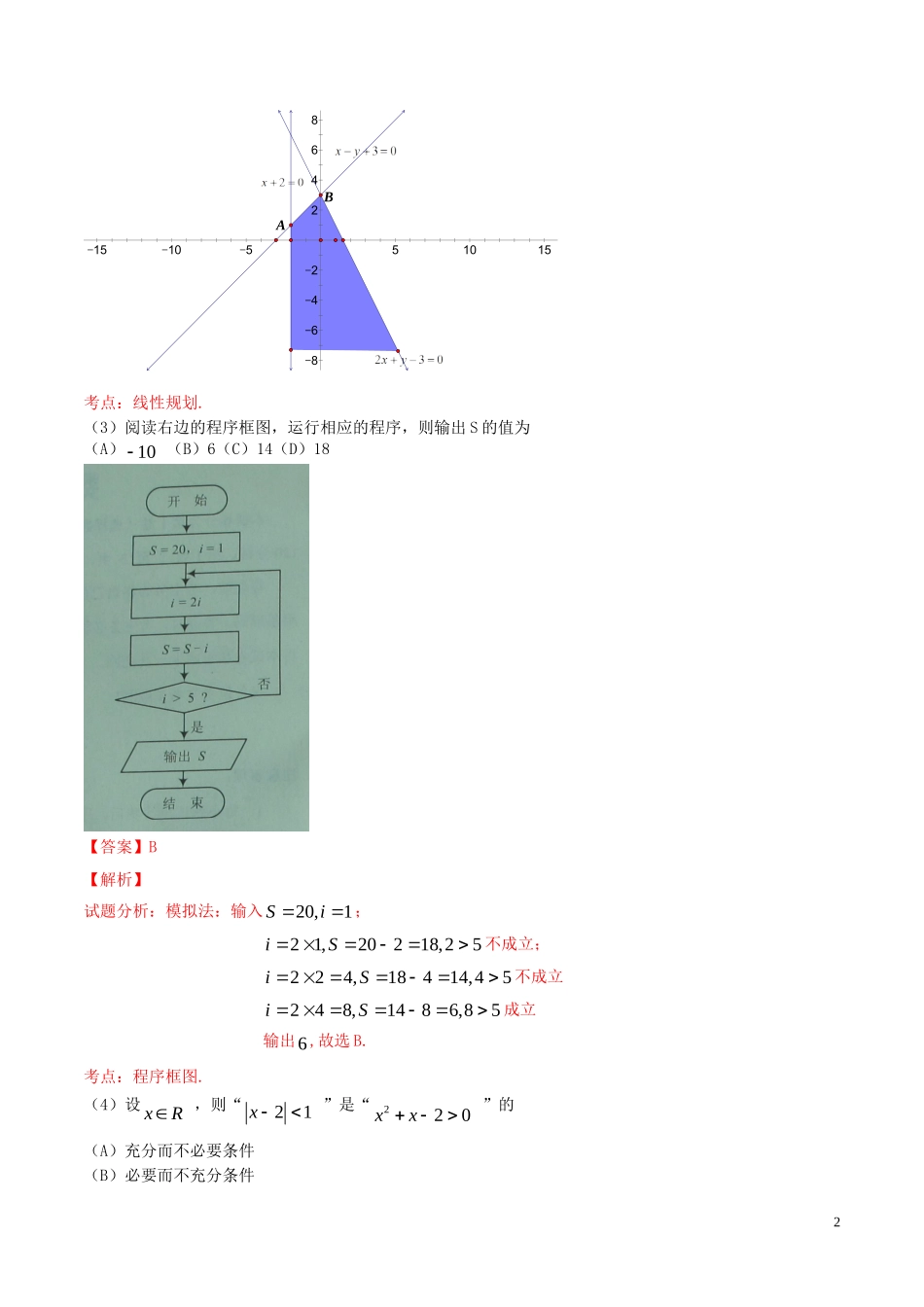
2015年普通高等学校招生全国统一考试数学理试题（天津卷，含解析）第I卷注意事项：1、每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.2、本卷共8小题，每小题5分，共40分.一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知全集1,2,3,4,5,6,7,8U，集合2,3,5,6A，集合1,3,4,6,7B，则集合UABð（A）2,5（B）3,6（C）2,5,6（D）2,3,5,6,8【答案】A【解析】试题分析：{2,5,8}UBð,所以{2,5}UABð，故选A.考点：集合运算.（2）设变量,xy满足约束条件2030230xxyxy，则目标函数6zxy的最大值为（A）3（B）4（C）18（D）40【答案】C1864224681510551015AB考点：线性规划.（3）阅读右边的程序框图，运行相应的程序，则输出S的值为（A）10（B）6（C）14（D）18【答案】B【解析】试题分析：模拟法：输入20,1Si；21,20218,25iS不成立；224,18414,45iS不成立248,1486,85iS成立输出6,故选B.考点：程序框图.（4）设xR，则“21x”是“220xx”的（A）充分而不必要条件（B）必要而不充分条件2（C）充要条件（D）既不充分也不必要条件【答案】A考点：充分条件与必要条件.（5）如图，在圆O中，,MN是弦AB的三等分点，弦,CDCE分别经过点,MN.若2,4,3CMMDCN，则线段NE的长为（A）83（B）3（C）103（D）52EDOABMNC【答案】A【解析】试题分析：由相交弦定理可知，,AMMBCMMDCNNEANNB，又因为,MN是弦AB的三等分点，所以AMMBANNBCNNECMMD，所以24833CMMDNECN，故选A.考点：相交弦定理.（6）已知双曲线222210,0xyabab的一条渐近线过点2,3，且双曲线的一个焦点在抛物线247yx的准线上，则双曲线的方程为（A）2212128xy（B）2212821xy（C）22134xy（D）22143xy【答案】D3考点：1.双曲线的标准方程及几何性质；2.抛物线的标准方程及几何性质.（7）已知定义在R上的函数21xmfx（m为实数）为偶函数，记0.52(log3),log5,2afbfcfm，则,,abc的大小关系为（A）abc（B）acb（C）cab（D）cba【答案】C【解析】试题分析：因为函数21xmfx为偶函数，所以0m，即21xfx，所以221loglog330.521(log3)log2121312,3aff2log502log5214,2(0)210bfcfmf所以cab，故选C.考点：1.函数奇偶性；2.指数式、对数式的运算.（8）已知函数22,2,2,2,xxfxxx函数2gxbfx，其中bR，若函数yfxgx恰有4个零点，则b的取值范围是（A）7,4（B）7,4（C）70,4（D）7,24【答案】D【解析】试题分析：由22,2,2,2,xxfxxx得222,0(2),0xxfxxx，4所以222,0()(2)42,0222(2),2xxxyfxfxxxxxxx，即222,0()(2)2,0258,2xxxyfxfxxxxx()()()(2)yfxgxfxfxb,所以yfxgx恰有4个零点等价于方程()(2)0fxfxb有4个不同的解，即函数yb与函数()(2)yfxfx的图象的4个公共点，由图象可知724b.864224681510551015考点：1.求函数解析式；2.函数与方程；3.数形结合.第II卷注意事项：1、用黑色墨水的钢笔或签字笔将答案写在答题卡上.2、本卷共12小题，共计110分.二、填空题：本大题共6小题，每小题5分，共30分.（9）i是虚数单位，若复数12iai是纯虚数，则实数a的值为.【答案】2【解析】试题分析：12212iaiaai是纯度数，所以20a，即2a.考点：1.复数相关定义；2.复数运算.5（10）一个几何体的三视图如图所示（单位：m），则该几何体的体积为3m.【答案】83【解析】试题分析：由三视图可知，该几何体是中间为...