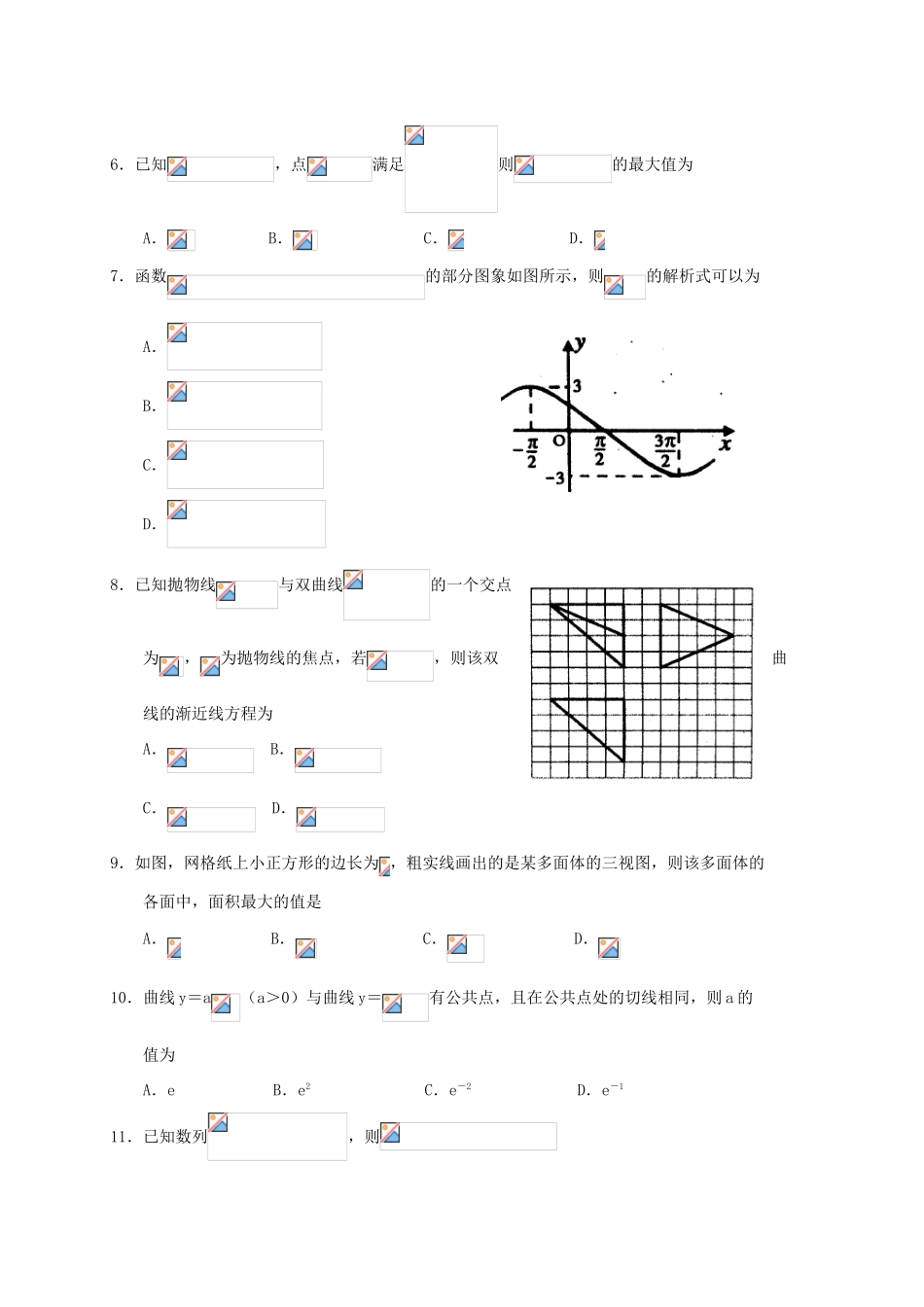
商丘市2016年高三5月第三次模拟考试数学(文科)本试卷分试题卷和答题卡两部分。试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共4页;答题卡共6页。满分为150分,考试时间为120分钟。考生作答时,请按要求把答案涂、写在答题卡规定的范围内,超出答题框或答在试题卷上的答案无效。考试结束只收答题卡。第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集,集合,,则A.B.C.D.2.若复数(其中是虚数单位)的实部与虚部相等,则A.B.C.D.3.下列函数中,满足的单调递增函数是A.B.C.D.4.若四点共线,且满足,则A.B.C.D.5.要计算的结果,下面程序框图中的判断框内可以填A.B.C.D.6.已知,点满足则的最大值为A.B.C.D.7.函数的部分图象如图所示,则的解析式可以为A.B.C.D.8.已知抛物线与双曲线的一个交点为,为抛物线的焦点,若,则该双曲线的渐近线方程为A.B.C.D.9.如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的值是A.B.C.D.10.曲线y=a(a>0)与曲线y=有公共点,且在公共点处的切线相同,则a的值为A.eB.e2C.e-2D.e-111.已知数列,则A.B.C.D.12.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数被称为狄利克雷函数,其中为实数集,为有理数集,则关于函数有如下四个命题:①;②函数是偶函数;③任取一个不为零的有理数,对任意的恒成立;④存在三个点使得为等边三角形.其中真命题的个数为A.B.C.D.第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分。第13题-第21题为必考题,每个试题考生都必须做答。第22题-第24题为选做题,考生根据要求做答。二、填空题(本大题共4小题,每小题5分,共20分)13.已知的取值如下表所示:从散点图分析,与线性相关,且,则_______.14.在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯”.这首古诗描述的这个宝塔其古称浮屠,本题说它一共有层,每层悬挂的红灯数是上一层的倍,共有盏灯,问塔顶有几盏灯?你算出顶层有______盏灯.15.已知抛物线的焦点恰好是椭圆的右焦点,且这两条曲线交点的连线过点,则该椭圆的离心率为______.16.设函数.有下列五个命题:①若对任意,关于的不等式恒成立,则;②若存在,使得不等式成立,则;③若对任意及任意,不等式恒成立,则;④若对任意,存在,使得不等式成立,则;⑤若存在及,使得不等式成立,则.其中,所有正确结论的序号为______.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)在中,分别为内角的对边,且.(Ⅰ)求角的大小;(Ⅱ)若的面积为,求边长的最小值.18.(本小题满分12分)如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况,该题满分为分.已知甲、乙两组的平均成绩相同,乙组某个数据的个位数模糊,记为.(Ⅰ)求的值,并判断哪组学生成绩更稳定;(Ⅱ)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于分的概率.19.(本小题满分12分)如图,在四棱锥中,底面是菱形,,,底面,是的中点,是的中点.(Ⅰ)求证:平面;(Ⅱ)求三棱锥的体积.20.(本小题满分12分)过点作直线与圆交于两点,在线段上取满足的点.(Ⅰ)求点的轨迹方程;(Ⅱ)设直线与圆交于两点,求为圆心)面积的最大值.21.(本小题满分12分)已知函数.(Ⅰ)求函数的单调区间和极值;(Ⅱ)若时,恒成立,求实数的取值范围.请考生在第22、23、24三题中任选一题做答,如果多做.则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。22.(本小题满分10分)选修4—1:几何证明选讲已知四边形ABCD为圆O的内接四边形,且BC=CD,其对角线AC与BD相交于点M,过点B作圆O的切线交DC的延长线于点P.(Ⅰ)求证:AB·MD=AD·BM;(Ⅱ)若CP·MD=CB·BM,求证:AB=BC.23.(本小题满分10分)选修4...