厦门市内厝中学高三（理）数学模拟试卷参考答案VIP免费

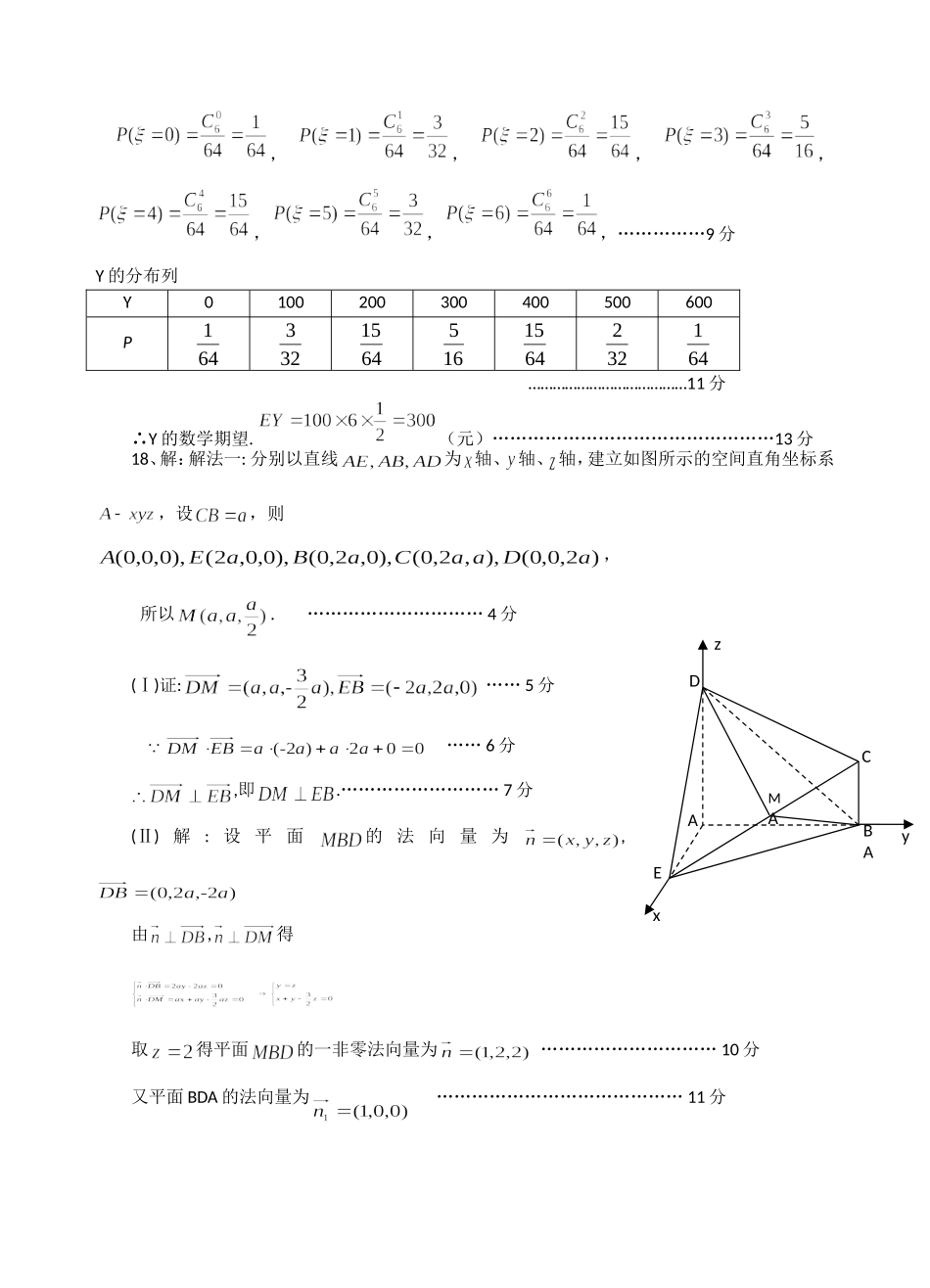
厦门市内厝中学高三（理）数学模拟试卷参考答案一、选择题：1-5DBCDA6-10BCACA二、填空题：11、5312、22013、14、115、设ha,hb,hc，三棱锥A-BCD四个面上的高.P为三棱锥A-BCD内任一点,P到相应四个面的距离分别为pa,pb,pc,我们可以得到结论:三、解答题：（本大题共6小题，共80分）16、解：（1）-----------------------------------------6分1,||22T-----------------------------------------8分（2）由（1）21)62sin()(xxf30x，1)62sin(21x----------------------------------------11分)(xf的值域是23,1--------------------------------------------------13分17、解：（1）用随机变量X表示面ABB1A1有X只灯发光；∴面ABB1A1需要维修的概率为…………………………6分（2）用ξ表示维修一次的面数因为ξ的取值为0，1，2，3，4，5，6且)21,6(~B∴，，，，，，，……………9分Y的分布列Y0100200300400500600P64132364151656415322641…………………………………11分∴Y的数学期望.（元）…………………………………………13分18、解：解法一:分别以直线为轴、轴、轴，建立如图所示的空间直角坐标系，设，则，所以.…………………………4分(Ⅰ)证:……5分……6分,即.………………………7分(Ⅱ)解:设平面的法向量为,由,得取得平面的一非零法向量为…………………………10分又平面BDA的法向量为……………………………………11分zyxEDCBAAMA，∴二面角的余弦值为.……………………………13分19、解：（Ⅰ）设椭圆的半焦距为c，依题意633caa，，∴1b，∴所求椭圆方程为2213xy．……………4分（Ⅱ）设11()Axy，，22()Bxy，．（1）当ABx⊥轴时，3AB．……………5分（2）当AB与x轴不垂直时，设直线AB的方程为ykxm．由已知2321mk，得223(1)4mk．……………7分把ykxm代入椭圆方程，整理得222(31)6330kxkmxm，122631kmxxk，21223(1)31mxxk．……………9分22221(1)()ABkxx22222223612(1)(1)(31)31kmmkkk22222222212(1)(31)3(1)(91)(31)(31)kkmkkkk2422212121233(0)34196123696kkkkkk．……………11分当且仅当2219kk，即33k时等号成立．当0k时，3AB，综上所述max2AB．当AB最大时，AOB△面积取最大值max133222SAB．……………13分20、解：(1)因x=1是()2lnbfxxxx的一个极值点,∴0)1('f又xxbxf12)('2所以2+b+1=0b=-∴3经检验，适合题意，所以b=-3．……………4分(2)0132)('2xxxf又0x∴x>1∴函数的单调增区间为),1[……………8分（3）xxfxg3)()(=2x+lnx……………9分设过点（2，5）与曲线g(x)的切线的切点坐标为00(,)xy∴/0005()(2)ygxx即000012ln5(2)(2)xxxx∴002ln20xx……………11分令h(x)=2ln2xx∴/h(x)=212xx=0∴2xh(∴x)在（0，2）上单调递减，在（2，）上单调递增又1()2ln202h，h(2)=ln2-1<0，222()0heeh(∴x)与x轴有两个交点∴过点（2，5）可作2条曲线y=g(x)的切线.……………14分21、1）(本小题满分7分）选修4——2：矩阵与变换解一：设A∴∴∴B＝解二：设则故（2）(本小题满分7分）选修4——4：坐标系与参数方程解：曲线C1可化为：曲线C2可化为联立解得交点为