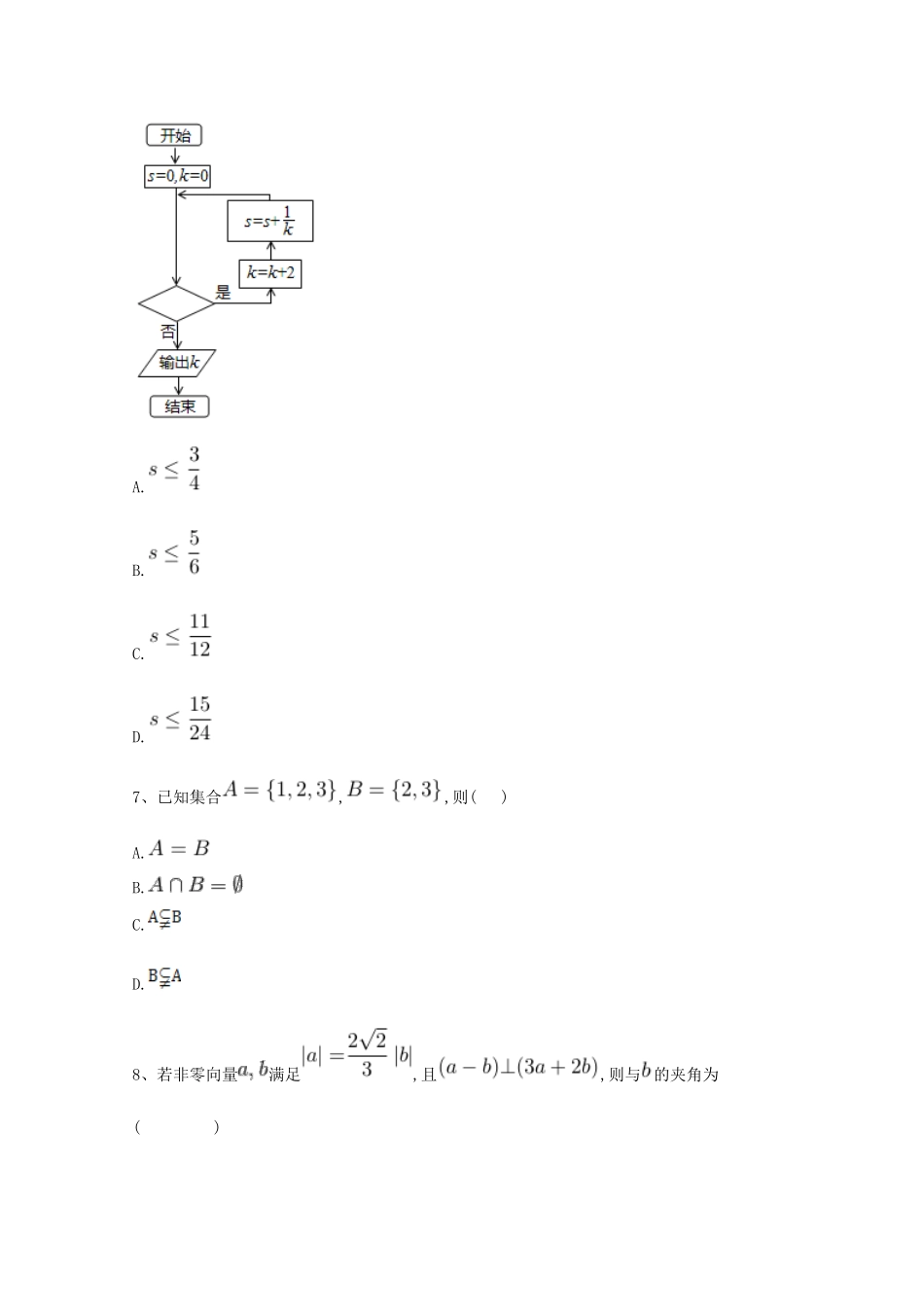
精品模拟卷(3)第1卷评卷人得分一、选择题1、化简的值为()A.B.C.D.2、命题"对任意都有"的否定是()A.对任意,都有B.不存在,使得C.存在,使得D.存在,使得3、设、是双曲线的左、右两个焦点,若双曲线右支上存在一点P,使(O为坐标原点)且则的值为()A.B.C.D.4、某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.5、重庆市年各月的平均气温(℃)数据的茎叶图如下:则这组数据的中位数是()A.B.C.D.6、执行如图所示的程序框图,若输入的值为8,则判断框图可填入的条件是()A.B.C.D.7、已知集合,,则()A.B.C.D.8、若非零向量满足,且,则与的夹角为()A.B.C.D.9、已知直线是圆的对称轴.过点作圆的一条切线,切点为,则()A.B.C.D.10、若,则()A.1B.2C.3D.411、""是""的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件12、已知i是虚数单位,复数z满足,则z的模是()A.B.C.D.评卷人得分二、填空题13、的展开式中的系数是_________.(用数字作答)14、在中,,,的角平分线,则_______.15、如图,圆的弦相交于点,过点作圆的切线与的延长线交于点,若,则.16、已知直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,则直线与曲线的交点的极坐标为.评卷人得分三、解答题17、设函数.1.求不等式的解集;2.若,恒成立,求实数的取值范围.18、如图,三棱锥中,平面,,,分别为线段,上的点,且,.1.证明:平面;2.求二面角的余弦值.19、(本小题满分12分,(1)小问4分,(2)小问8分)在数列中,(1)若求数列的通项公式;(2)若证明:20、在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的参数方程为(t为参数),直线l的极坐标方程为.1.写出曲线C的普通方程和直线l的直角坐标方程;2.设曲线C与直线l的交点为A、B两点,求△OAB(O为坐标原点)的面积.21、在直角坐标系中,以原点为极点、以轴的正半轴为极轴建立极坐标系,已知曲线的极坐标方程为.1.求曲线的直角坐标方程并指出其形状;2.设是曲线上的动点,求的取值范围.22、设函数.1.若在处取得极值,确定的值,并求此时曲线在点处的切线方程;2.若在上为减函数,求的取值范围.23、已知函数,1.求函数的对称中心2.已知在中,角、、所对的边分别为、、,且,的外接圆半径为,求周长的最大值参考答案一、选择题1.答案:A2.答案:D解析:由全称命题的否定知,命题"对任意都有"的否定是"存在,使得",故选D3.答案:A4.答案:B解析:由三视图可知该几何体是由一个底面半径为,高为的圆柱,再加上一个半圆锥:其底面半径为,高也为;构成的一个组合体,故其体积为;故选B.5.答案:B解析:从茎叶图知所有数据为中间两个数为,故中位数为,选.6.答案:C解析:由程序框图,的值依次为0,2,4,6,8,因此(此时)还必须计算一次,因此可填,选C.7.答案:D解析:由真子集的概念知,故选D.8.答案:A解析:设,则,. ,即,∴,∴. ,∴.故选.9.答案:C解析:圆标准方程为,圆心为,半径为,因此,,即,.选C.10.答案:C解析:11.答案:A解析:当时,;同时当时,可得;可得“”是“”的充要条件.考点:充分、必要条件的判断.本题主要考查的是一元二次不等式、对数不等式和集合的交集、并集和补集运算,属于容易题.解不等式时一定要注意对数的真数大于0和的系数大于0,否则很容易出现错误.12.答案:C解析:解:由=i,得(1+i)z=i,∴,∴.∴选C.二、填空题13.答案:84解析: 的展开式中的系数是14.答案:解析:由正弦定理得,即,解得,从而,所以,.15.答案:2解析:设,则. 为的切线,∴,即∴.由相交弦定理得,,即,∴.16.答案:(2,π)解析:直线的普通方程为,曲线的直角坐标系为,故直线与曲线的交点为,对应极坐标为.三、解答题17.答案:1.由题意得,当时,不等式化为,解得,当时,不等式化为,解得,∴,当时,不等式化为,解得,∴.综上,不等式的解集为或2.由1得,解得,综上,的取值范围为.18.答案:1.由平面,平面,得,由,得为等腰直角三角形,故。又,所以平面。2.由1知,为等腰直角三角形,,如图,过作垂直于,易知,又,故。由得,,故,以为坐标原点,分别以,,的方向为轴,轴,轴的正方形建立空间直角坐标系,则,,,,,,,。设平面的法向量为,由,,得故可...