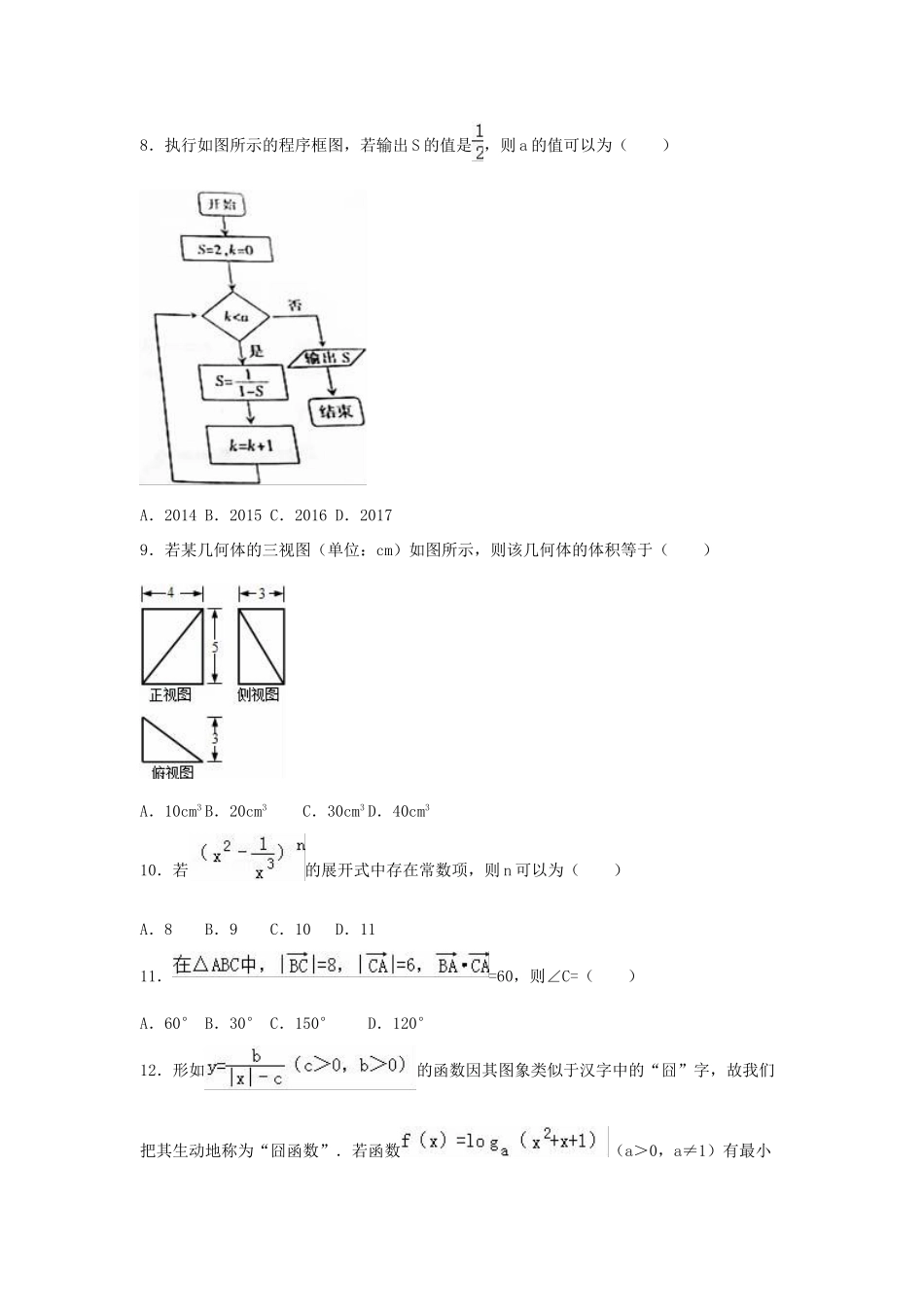
2016年广东省茂名市高考数学一模试卷(理科)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数(i为虚数单位)的虚部是()A.2iB.﹣2iC.﹣2D.22.下列函数在其定义域上既是奇函数又是减函数的是()A.f(x)=2xB.f(x)=xsinxC.D.f(x)=﹣x|x|3.已知cos(α﹣π)=,﹣π<α<0,则tanα=()A.B.C.D.﹣4.设双曲线﹣x2=1上的点P到点(0,)的距离为6,则P点到(0,﹣)的距离是()A.2或10B.10C.2D.4或85.下列有关命题说法正确的是()A.命题p:“∃x∈R,sinx+cosx=”,则¬p是真命题B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C.命题“∃x∈R,使得x2+x+1<0“的否定是:“∀x∈R,x2+x+1<0”D.“a>l”是“y=logax(a>0且a≠1)在(0,+∞)上为增函数”的充要条件6.将函数的图象向右平移个单位得到函数g(x)的图象,则g(x)的一条对称轴方程可以为()A.B.C.D.7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,这6名学生要排成一排合影,则同校学生排在一起的概率是()A.B.C.D.8.执行如图所示的程序框图,若输出S的值是,则a的值可以为()A.2014B.2015C.2016D.20179.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.10cm3B.20cm3C.30cm3D.40cm310.若的展开式中存在常数项,则n可以为()A.8B.9C.10D.1111.=60,则∠C=()A.60°B.30°C.150°D.120°12.形如的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数(a>0,a≠1)有最小值,则当c,b的值分别为方程x2+y2﹣2x﹣2y+2=0中的x,y时的“囧函数”与函数y=loga|x|的图象交点个数为()A.1B.2C.4D.6二.填空题:本大题共4小题,每小题5分,共20分.13.一个长方体高为5,底面长方形对角线长为12,则它外接球的表面积为.14.探照灯反射镜的纵断面是抛物线的一部分,光源在抛物线的焦点,已知灯口直径是60cm,灯深40cm,则光源到反射镜顶点的距离是cm.15.已知点P(x,y)的坐标满足条件,那么(x+1)2+y2的取值范围为.16.在△ABC中,D为AB的一个三等分点,AB=3AD,AC=AD,CB=3CD,则cosB=.三.解答题:本大题共5小题,每题12分共60分.解答应写出文字说明,证明过程或演算步骤.17.已知{bn}为单调递增的等差数列,b3+b8=26,b5b6=168,设数列{an}满足(1)求数列{bn}的通项;(2)求数列{an}的前n项和Sn.18.已知圆锥曲线C:(α是参数)和定点A(0,),F1,F2分别是曲线C的左、右焦点.(1)以原点为极点,x轴的正半轴为极轴建立坐标系,求直线AF2的极坐标系方程.(2)若P是曲线C上的动点,求||•||的取值范围.19.如图,ABCD是平行四边形,EA⊥平面ABCD,PD∥EA,BD=PD=2EA=4,AD=3,AB=5.F,G,H分别为PB,EB,PC的中点.(1)求证:DB⊥GH;(2)求平面FGH与平面EBC所成锐二面角的余弦值.20.已知椭圆离心率为,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:相切.(1)求椭圆C的方程;(2)设不过原点O的直线l2与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.21.已知定义在R上的偶函数f(x),当x∈[0,+∞)时,f(x)=ex.(1)当x∈(﹣∞,0)时,求过原点与函数f(x)图象相切的直线的方程;(2)求最大的整数m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤ex.请在第22.23.24题中任选一题作答,如果多做,则按所做的第一题记分,解答时请写清题号.选修4-1,几何证明选讲22.如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1(1)求证:CB为∠ACD的角平分线;(2)求圆O的直径的长度.选修4-4:极坐标与参数方程23.在直角坐标系xOy中,直线l的方程为x+y﹣8=0,曲线C的参数方程为.(1)已知极坐标系与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴,若点P的极坐标为,请判断点P与曲线C的位置关系;(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值与最...