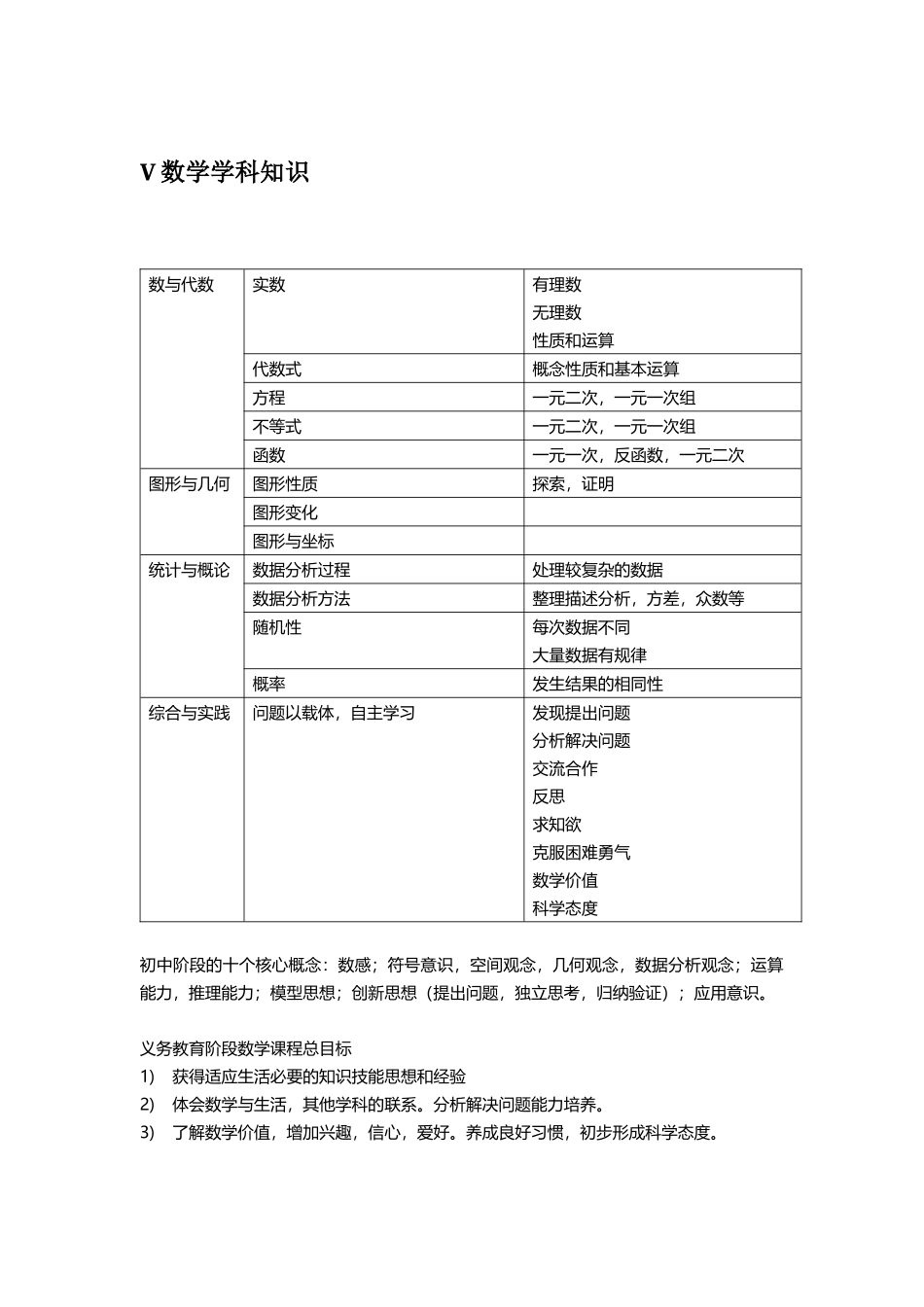
V数学学科知识数与代数实数有理数无理数性质和运算代数式概念性质和基本运算方程一元二次,一元一次组不等式一元二次,一元一次组函数一元一次,反函数,一元二次图形与几何图形性质探索,证明图形变化图形与坐标统计与概论数据分析过程处理较复杂的数据数据分析方法整理描述分析,方差,众数等随机性每次数据不同大量数据有规律概率发生结果的相同性综合与实践问题以载体,自主学习发现提出问题分析解决问题交流合作反思求知欲克服困难勇气数学价值科学态度初中阶段的十个核心概念:数感;符号意识,空间观念,几何观念,数据分析观念;运算能力,推理能力;模型思想;创新思想(提出问题,独立思考,归纳验证);应用意识。义务教育阶段数学课程总目标1)获得适应生活必要的知识技能思想和经验2)体会数学与生活,其他学科的联系。分析解决问题能力培养。3)了解数学价值,增加兴趣,信心,爱好。养成良好习惯,初步形成科学态度。数学在义务教育的地位。义务教育具有基础性发展性和普及性。数学课程能使学生掌握以后生活工作必备的基本知识,基本技能,思想方法;抽象能力和推理能力;促进情感态度价值观健康发展。为今后的生活,学习打下基础。二次根式:就是开根号目标:了解意义,掌握字母取值问题,掌握性质灵活运用通过计算,培养逻辑思维能力领悟数学的对称性和规律美。重点:根式意义;难点;字母取值范围勾股定理探索证明的基础上,联系实际,归纳抽象,应用解决实际问题。通过探索分析归纳过程,提高逻辑能力和分析解决问题能力。数学好奇心,热爱数学。重点:应用难点:实际问题转化为数学问题平行四边形及性质经历探索平行四边形性质和概念,掌握性质,能够判别体会操作转化的思想过程,积累问题解决的思想。与他人交流,积极动手的习惯四边形内角和:量角器;内部做三角形;按照边做三角形;按照定点做三角形。一次函数和二元一次方程的关系。数形结合数学思想为主体;问题为贯穿;数形结合为工具;提高问题解决能力。数学课程理念内涵:人人获得良好数学教育,在数学上得到不同发展内容:符合数学特点,认知规律,社会实际。层次性和多样性。间接与直接。过程:师生交往评价:多元发展信息技术与课程:现在信息技术改进教学方法,资源。1)信息技术开发资源,注重整合2)教学方式的改善3)理解原理的基础上,利用计算器,计算机4)不能完全替代原有的有段。合情推理:根据已有的结论,实践结果,直观等推测某些结论。便于发现问题。(归纳法n=1和n大于1成立的证明)演绎推理:根据已有的结论,严格按照逻辑进行推理,用于证明。从一般到特殊直接证明:原命题直接逐步推理的到新命题。间接证明:反证法数学教学目标明确解决三个问题:为什么学习数学,应当学那些,将给学生带来什么。数据课程核心概念数感,符号意识,空间概念,几何观念,数据分析观念,运算能力,推理能力,模型思想应用意识,创新意识。论述:数学学科内涵是影响数学课程的主义因素,以一元二次论述内涵的意义。1)数学本身的内涵即知识方法和意义。2)一元二次方程有关概念基本解法和其他知识的联系,模型应用等。3)学科内涵作为教育任务,学习中可能存在困难。过程性目标与结果性目标分析初中数学学段目标的知识技能。数与代数:体验具体情景中数学符号的抽象过程,理解有理数,无理数,实数,方程,函数等;掌握必要的运算技能;探索变化规律,掌握表达方法。包含了过程性和结果性目标体验探索…….为过程性目标;掌握……为结果性目标图形与几何:掌握三角形,平行线,园,四边形基本性质判断,掌握基本作图技能,理解探索图形变化,投影,理解坐标系和位置。包含了包含了过程性和结果性目标。体验探索…….为过程性目标;掌握,理解……为结果性目标统计与概率:体验收集处理分析推断过程,理解抽样方法,体验用样本估计总体过程;进一步认识随机现象和概率。包含了包含了过程性和结果性目标。体验探索…….为过程性目标;掌握,理解……为结果性目标函数集中安排在不等式方程学习后不合理,函数学习不仅仅是掌握知识本身,还有认识现象,解决问题的方法;函数知识本身的内涵不单纯的包括定理定义等,...