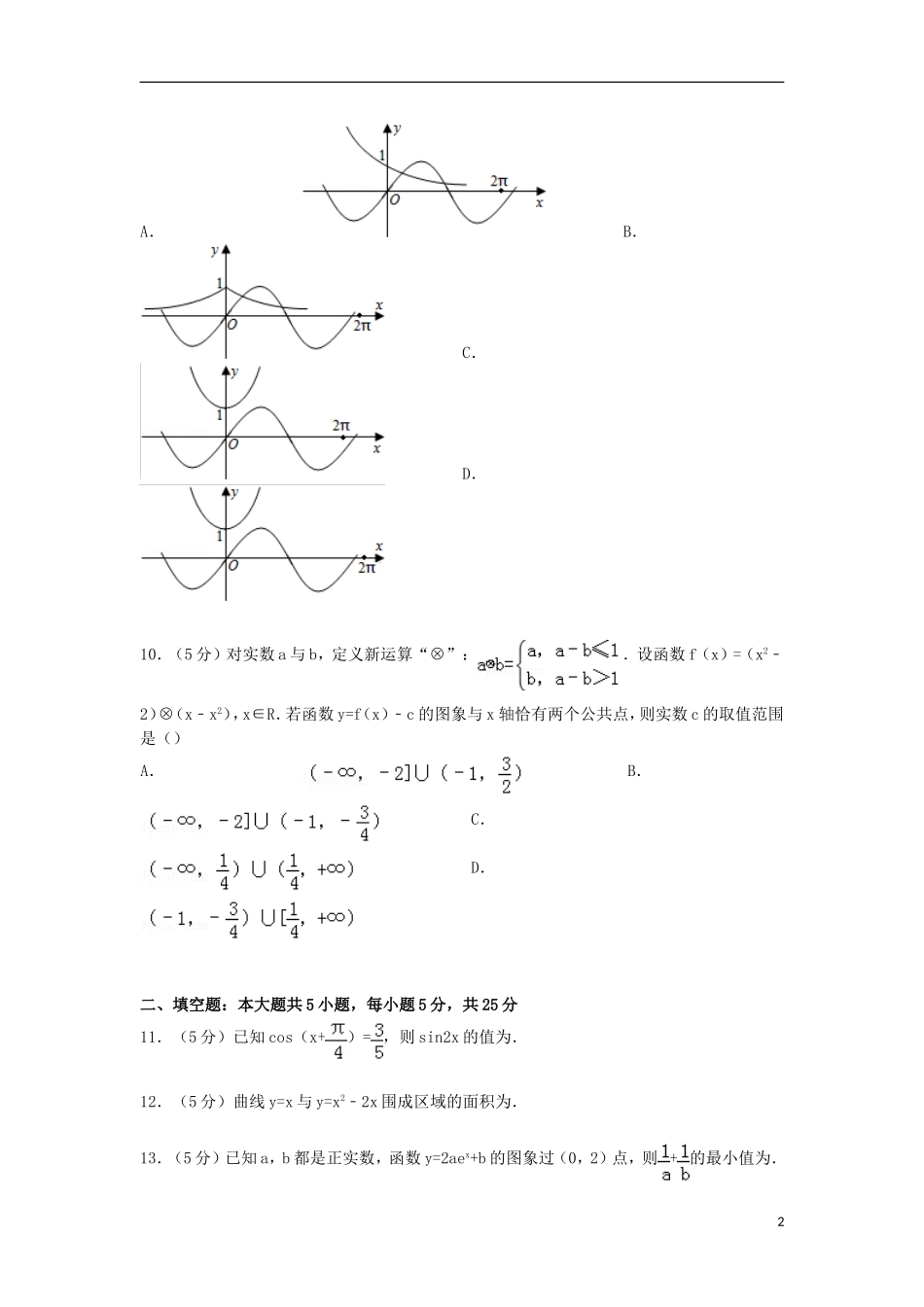
山东省青岛二中2015届高三上学期10月段考数学试卷(理科)一、选择题:本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知m、n∈R,则>成立的一个充要条件是()A.m>0>nB.n>m>0C.mn(m﹣n)<0D.m<n<02.(5分)已知集合M={a,b,c,d},N={﹣2,0,1},若f是从M到N的映射,且f(a)=0,f(b)=﹣2,则这样的映射f共有()A.4个B.6个C.9个D.以上都不对3.(5分)设f(x)=,则f(f())=()A.eB.1C.2D.以上都不对4.(5分)若logmn=﹣1,则3n+m的最小值是()A.2B.2C.2D.5.(5分)函数f(x)=sinx在区间上是增函数,且f(a)=﹣1,f(b)=1,则=()A.0B.C.﹣1D.16.(5分)设函数f(x)=logax(a>0且a≠1),若f(x1•x2•x3…x2015)=50,则f(x12)+f(x22)+f(x32)+…+f(x20152)的值等于()A.10B.100C.1000D.20157.(5分)设函数f(x)=,集合M={x|f(x)<0},P={x|f′(x)≥0},M是P的真子集,则实数a的取值范围是()A.(﹣∞,1)B.(0,1)C.(1,+∞)D.时,f(x)=x2﹣2x,则当x∈时,f(x)的最小值是()A.﹣1B.C.D.9.(5分)函数y=a|x|与y=sinax(a>0且a≠1)在同一直角坐标系下的图象可能是()1A.B.C.D.10.(5分)对实数a与b,定义新运算“⊗”:.设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是()A.B.C.D.二、填空题:本大题共5小题,每小题5分,共25分11.(5分)已知cos(x+)=,则sin2x的值为.12.(5分)曲线y=x与y=x2﹣2x围成区域的面积为.13.(5分)已知a,b都是正实数,函数y=2aex+b的图象过(0,2)点,则+的最小值为.214.(5分)已知偶函数y=f(x)(x∈R)满足f(x)=f(2﹣x),且当x∈时,f(x)=x2,则函数y=f(x)与y=log7x的图象的交点个数为.15.(5分)设函数f(x)=,对任意x1、x2∈(0,+∞),不等式恒成立,则正数k的取值范围是.三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤16.已知集合A={y|y=()x﹣3()x+1+1,x∈(﹣1,2)},B={x|x﹣m2|≥},命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.17.若函数f(x)=lnx,若对所有的x∈上的取值范围.19.已知函数f(x)=,其中a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在原点处的切线方程;(Ⅱ)求f(x)的单调增区间;(Ⅲ)若f(x)在(0,1)内有最大值,求a的取值范围.20.已知定义域为R的函数f(x)=是奇函数.(1)求a,b的值;(2)判断函数的单调性并证明;(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.21.已知函数f(x)=lnx+,其中a为大于零的常数.(Ⅰ)若函数f(x)在区间上的最小值;(Ⅲ)求证:对于任意的n≥2,n∈N*,都有lnn>++…+成立.山东省青岛二中2015届高三上学期10月段考数学试卷(理科)参考答案与试题解析3一、选择题:本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知m、n∈R,则>成立的一个充要条件是()A.m>0>nB.n>m>0C.mn(m﹣n)<0D.m<n<0考点:不等关系与不等式;必要条件、充分条件与充要条件的判断.分析:由题意m、n∈R,则>,可将其移项、通分进行等价化简,从而求解.解答:解: >∴﹣>0∴>0∴m•n(n﹣m)>0∴m•n(m﹣n)<0.故选C.点评:此题主要考查不等关系与不等式之间的关系及必要条件、充分条件和充要条件的定义,是一道基础题.2.(5分)已知集合M={a,b,c,d},N={﹣2,0,1},若f是从M到N的映射,且f(a)=0,f(b)=﹣2,则这样的映射f共有()A.4个B.6个C.9个D.以上都不对考点:映射.专题:函数的性质及应用.分析:根据映射的定义,结合已知可得当f(a)=0,f(b)=﹣2时,集合M中元素c在集合N中的象有三种情况;集合M中元素d在集合N中的象也有三种情况;进而可得答案.解答:解:若f是从M到N的映射,且f(a)=0,f(b)=﹣2,则集合M中元素c在集合N中的象...