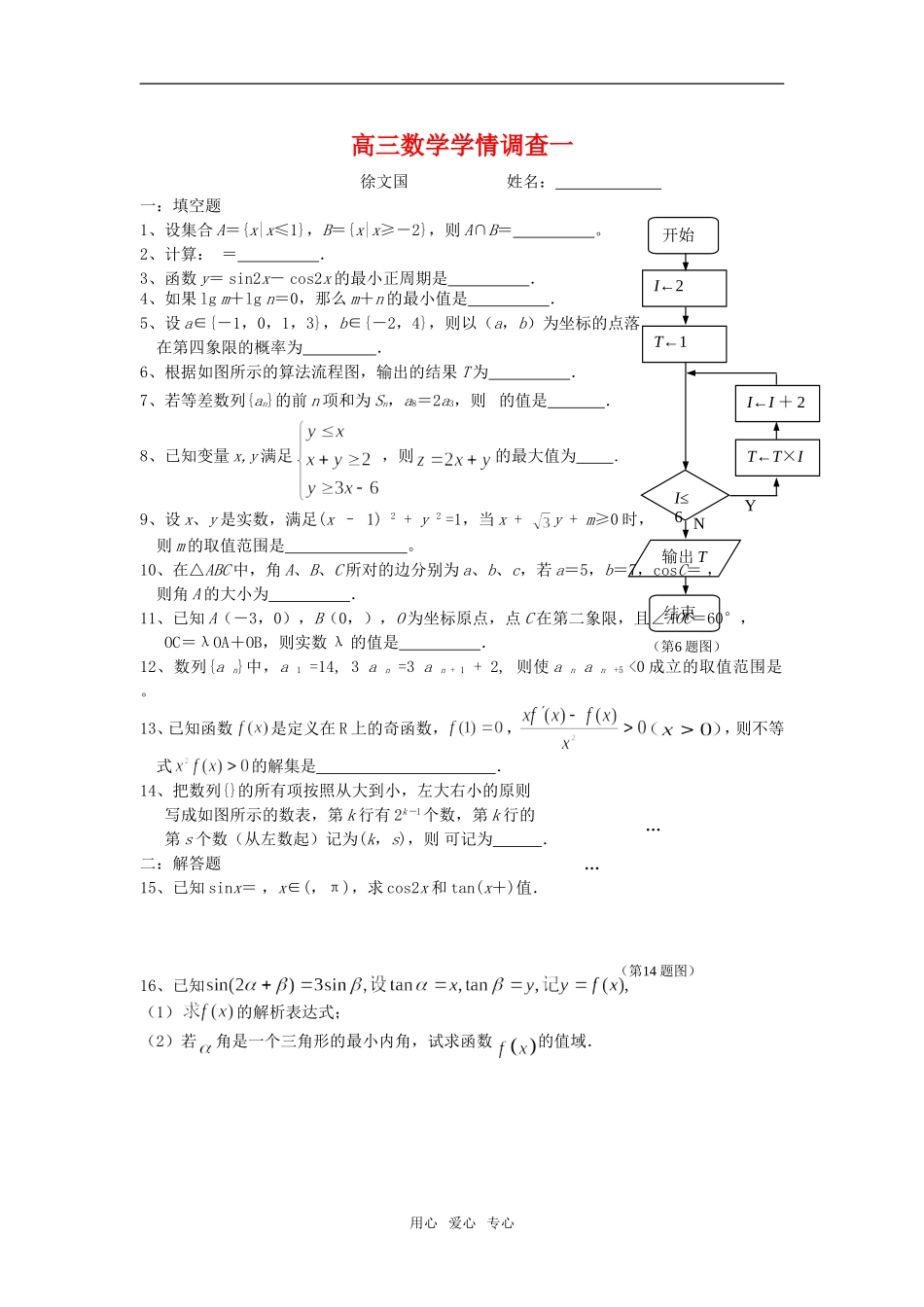
高三数学学情调查一徐文国姓名:一:填空题1、设集合A={x|x≤1},B={x|x≥-2},则A∩B=。2、计算:=.3、函数y=sin2x-cos2x的最小正周期是.4、如果lgm+lgn=0,那么m+n的最小值是.5、设a∈{-1,0,1,3},b∈{-2,4},则以(a,b)为坐标的点落在第四象限的概率为.6、根据如图所示的算法流程图,输出的结果T为.7、若等差数列{an}的前n项和为Sn,a8=2a3,则的值是.8、已知变量x,y满足,则的最大值为.9、设x、y是实数,满足(x–1)2+y2=1,当x+y+m≥0时,则m的取值范围是。10、在△ABC中,角A、B、C所对的边分别为a、b、c,若a=5,b=7,cosC=,则角A的大小为.11、已知A(-3,0),B(0,),O为坐标原点,点C在第二象限,且∠AOC=60°,OC=λOA+OB,则实数λ的值是.12、数列{an}中,a1=14,3an=3an+1+2,则使anan+5<0成立的取值范围是。13、已知函数是定义在R上的奇函数,,,则不等式的解集是.14、把数列{}的所有项按照从大到小,左大右小的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为(k,s),则可记为.二:解答题15、已知sinx=,x∈(,π),求cos2x和tan(x+)值.16、已知(1)的解析表达式;(2)若角是一个三角形的最小内角,试求函数的值域.用心爱心专心开始I←2T←1I≤6输出T结束T←T×II←I+2NY(第6题图)……(第14题图)17、某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式P=,Q=t.今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:(1)y关于x的函数表达式;(2)总利润的最大值.18、如图,在边长为1的正三角形中,分别是边上的点,若,.设的中点为,的中点为.⑴若三点共线,求证;⑵若,求的最小值.用心爱心专心ABCEFMN第18题19、已知:在数列{an}中,a1=,an+1=an+.(1)令bn=4nan,求证:数列{bn}是等差数列;(2)若Sn为数列{an}的前n项的和,Sn+λnan≥对任意n∈N*恒成立,求实数λ的最小值.20、已知,其中x∈R,为参数,且0≤≤。(1)当cos=0时,判断函数是否有极值;(2)要使函数的极小值大于零,求参数的取值范围;(3)若对(2)中所求的取值范围内的任意参数,函数在区间(2a–1,a)内都是增函数,求实数a的取值范围。用心爱心专心高三数学学情调查一参考答案一:填空题1、{x|-2≤x≤1}2、1+i3、π4、25、6、487、68、99、m≥110、11、12、{18,19,20,21}13、14、(10,494)二:解答题15、解:cos2x=1-2sin2x=1-2×()2=.………………………………………6分因为sinx=,x∈(,π),所以cosx=-=-.………………8分则tanx==-.……………………………………………………………10分所以tan(x+)==.…………………………………………………14分16、解:(1)由,得,…………………………2分,用心爱心专心,,于是,,∴,即.…………………………7分(2) 角是一个三角形的最小内角,∴0<≤,,………………10分设,则≥(当且仅当时取=),………12分故函数的值域为.………………………………14分17、解:(1)根据题意,得y=+(5-x),…………………………………………6分x∈[0,5].……………………………………………………………………7分(注:定义域写成(0,5)不扣分)(2)令t=,t∈[0,],则x=,y=-+t+=-(t-2)2+.…………………………………………………10分因为2∈[0,],所以当=2时,即x=时,y最大值=.…………………13分答:总利润的最大值是亿元.…………………………………………………………14分18、⑴由三点共线,得,…………………………2分设,即,………………………4分所以,所以.…………………………7分⑵因为=,又,所以,…………………………12分所以=故当时,.…………………………16分19、解:(1)由an+1=an+,得4n+1an+1=4nan+2.………………………………………………………………2分所以bn+1=bn+2,即bn+1-bn=2.…………………………………………………………………...