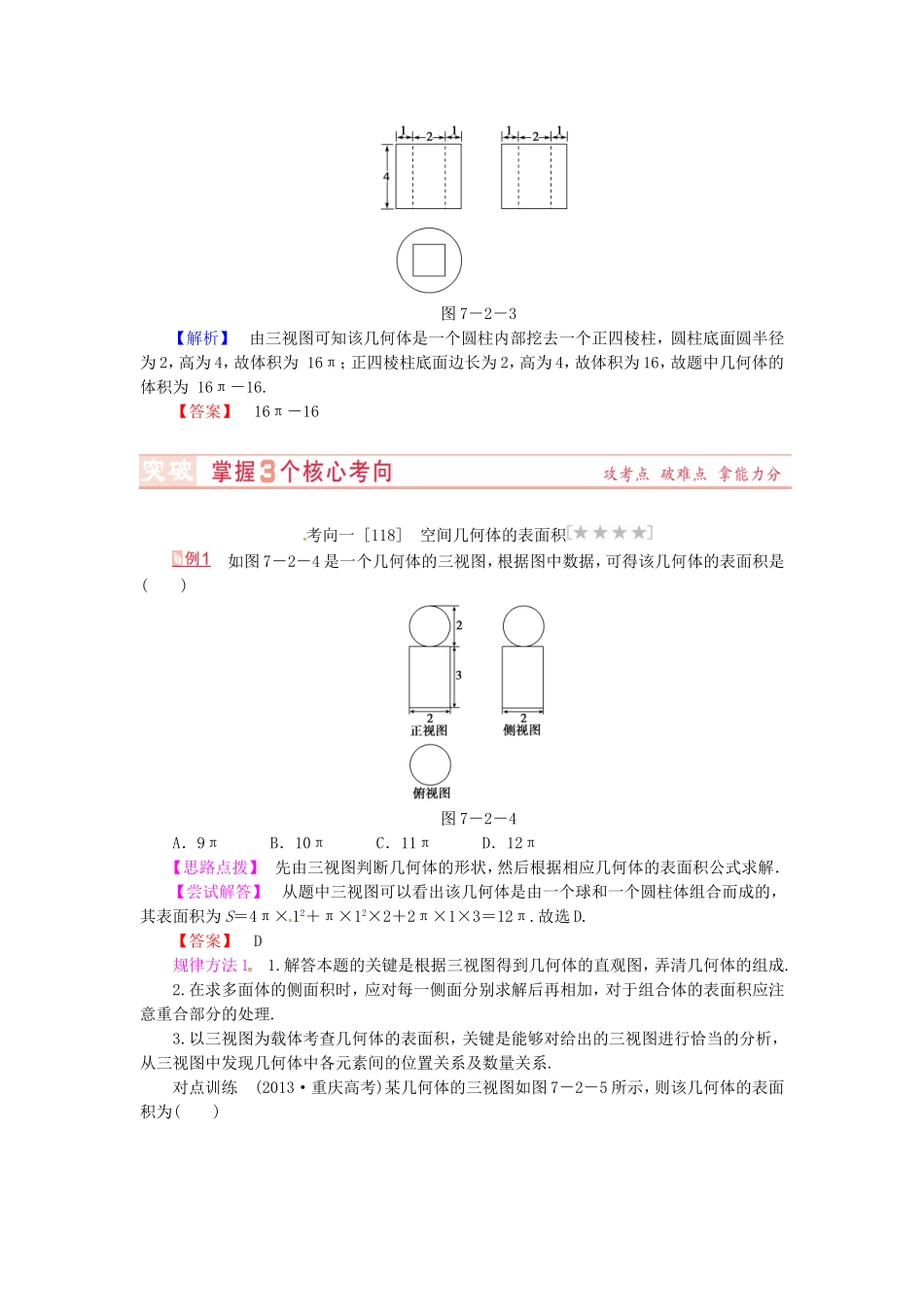
第二节空间几何体的表面积与体积[考情展望]1.与三视图相结合考查柱、锥、台、球的体积和表面积.2.以选择题与填空题形式考查.一、旋转体的表(侧)面积名称侧面积表面积圆柱(底面半径r,母线长l)2πrl2πr(l+r)圆锥(底面半径r,母线长l)πrlπr(l+r)圆台(上、下底面半径r,母线长l)π(r1+r2)lπ(r1+r2)l+π(r+r)球(半径为R)4πR2二、空间几何体的体积(h为高,S为下底面积,S′为上底面积)1.V柱体=Sh.2.V锥体=Sh.3.V台体=h(S++S′).4.V球=πR3(球半径是R).求几何体体积的两种重要方法1.割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.2.等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.1.正六棱柱的高为6,底面边长为4,则它的全面积为()A.48(3+)B.48(3+2)C.24(+)D.144【解析】正六棱柱的侧面积S侧=6×6×4=144,底面面积S底=2×6××42=48,∴S表=144+48=48(3+).【答案】A2.若一个底面是正三角形的三棱柱的正视图如图7-2-1所示,则其侧面积等于()图7-2-1A.B.2C.2D.6【解析】由三棱柱的正视图可知此三棱柱为底面边长为2,侧棱长为1的正三棱柱,∴S侧=2×1×3=6.【答案】D3.圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是()A.4πSB.2πSC.πSD.πS【解析】设圆柱的底面半径为r,则S=πr2,∴r=.由题意得圆柱的高h=2πr,∴S侧=2πr·h=4π2·=4πS.【答案】A4.母线长为1的圆锥的侧面展开图的面积是π,则该圆锥的体积为()A.πB.πC.πD.π【解析】设圆锥的底面半径为r,依题意得πr·1=π,∴r=.∴圆锥的高h==.∴圆锥的体积V=πr2h=π.【答案】C5.(2013·陕西高考)某几何体的三视图如图7-2-2所示,则其表面积为________.图7-2-2【解析】由三视图可知,该几何体为一个半径为1的半球,其表面积为半个球面面积与截面面积的和,即×4π+π=3π.【答案】3π6.(2013·辽宁高考)某几何体的三视图如图7-2-3所示,则该几何体的体积是________.图7-2-3【解析】由三视图可知该几何体是一个圆柱内部挖去一个正四棱柱,圆柱底面圆半径为2,高为4,故体积为16π;正四棱柱底面边长为2,高为4,故体积为16,故题中几何体的体积为16π-16.【答案】16π-16考向一[118]空间几何体的表面积如图7-2-4是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()图7-2-4A.9πB.10πC.11πD.12π【思路点拨】先由三视图判断几何体的形状,然后根据相应几何体的表面积公式求解.【尝试解答】从题中三视图可以看出该几何体是由一个球和一个圆柱体组合而成的,其表面积为S=4π×12+π×12×2+2π×1×3=12π.故选D.【答案】D规律方法11.解答本题的关键是根据三视图得到几何体的直观图,弄清几何体的组成.2.在求多面体的侧面积时,应对每一侧面分别求解后再相加,对于组合体的表面积应注意重合部分的处理.3.以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.对点训练(2013·重庆高考)某几何体的三视图如图7-2-5所示,则该几何体的表面积为()图7-2-5A.180B.200C.220D.240【解析】由三视图知识知该几何体是底面为等腰梯形的直四棱柱.等腰梯形的上底长为2,下底长为8,高为4,腰长为5,直四棱柱的高为10,所以S底=×(8+2)×4×2=40,S侧=10×8+10×2+2×10×5=200,S表=40+200=240,故选D.【答案】D考向二[119]空间几何体的体积(1)(2013·课标全国卷Ⅰ)某几何体的三视图如图7-2-6所示,则该几何体的体积为()图7-2-6A.16+8πB.8+8πC.16+16πD.8+16π图7-2-7(2)(2012·山东高考)如图7-2-7,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________...