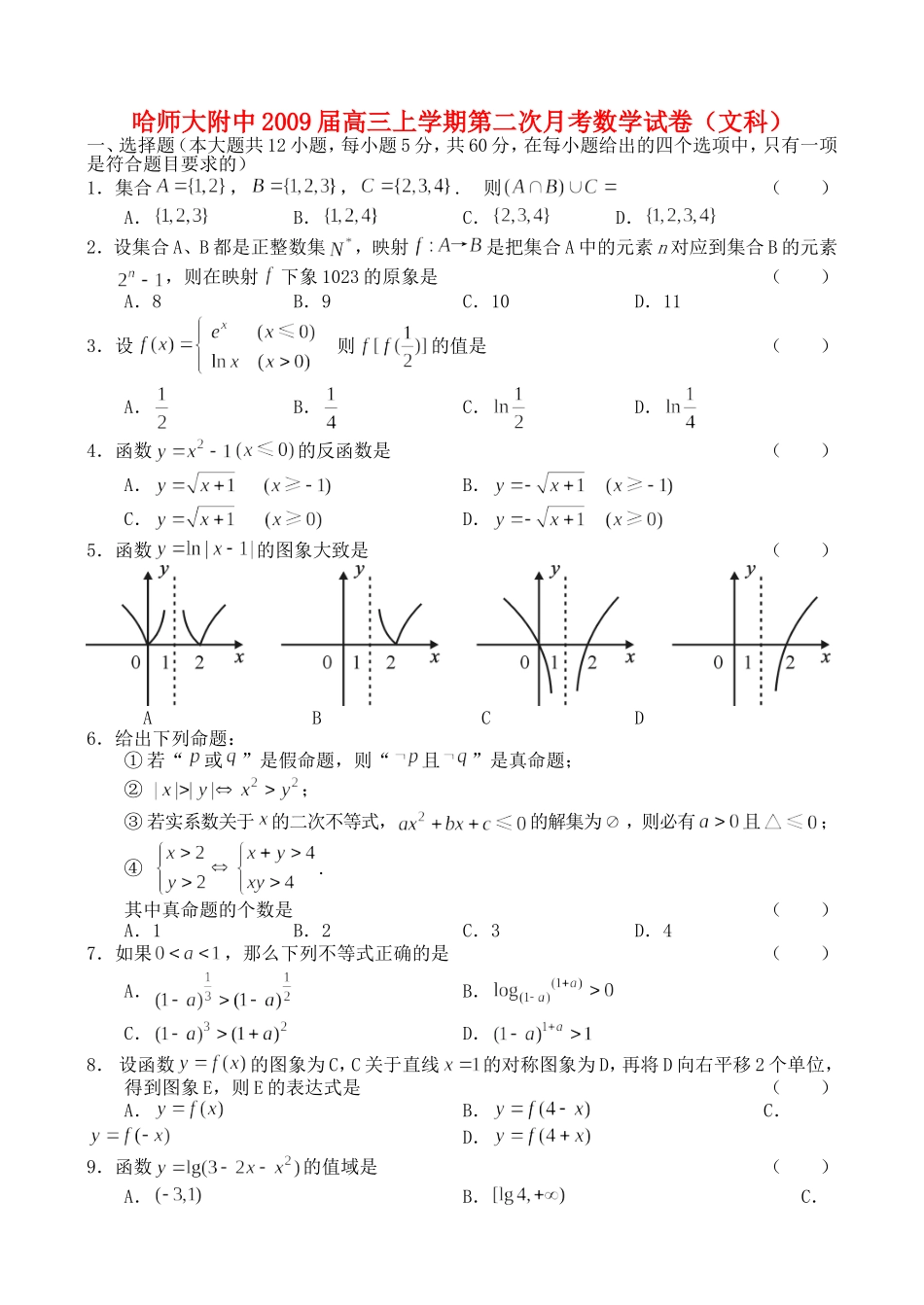
哈师大附中2009届高三上学期第二次月考数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合,,.则()A.B.C.D.2.设集合A、B都是正整数集,映射是把集合A中的元素n对应到集合B的元素,则在映射下象1023的原象是()A.8B.9C.10D.113.设则的值是()A.B.C.D.4.函数的反函数是()A.B.C.D.5.函数的图象大致是()ABCD6.给出下列命题:①若“或”是假命题,则“且”是真命题;②;③若实系数关于的二次不等式,的解集为,则必有且;④.其中真命题的个数是()A.1B.2C.3D.47.如果,那么下列不等式正确的是()A.B.C.D.8.设函数的图象为C,C关于直线的对称图象为D,再将D向右平移2个单位,得到图象E,则E的表达式是()A.B.C.D.9.函数的值域是()A.B.C.D.10.已知函数是以2为周期的偶函数,且当时,则在内的解析式是()A.B.C.D.11.设且.那么()A.B.C.D.12.已知是R上的偶函数,且在区间上是增函数,若,那么实数的取值范围是()A.B.C.D.二、填空题(本大题共4小题,每小题4分共16分,请把答案填在题中的横线上)13.函数的定义域是.14.函数的定义域为R,则两函数的图象关于对称。15.在函数、、、这四个函数中,当时,使恒成立的函数是.16.设,满足,,且,,则.三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)设集合、,全集为R.(1)当时,求:;(2)若,求实数的取值范围.18.(本小题满分12分)设,为奇函数(1)确定的值;(2)用定义证明:在R上为增函数.826119.(本小题满分12分)已知二次函数的图象过点,且与直线切于点(1)求的表达式;(2)试比较与的大小.20.(本小题满分12分)设定义在R上的函数,对任意,都有,且当时,,.(1)证明:为奇函数;(2)求:在上的最大值和最小值;(3)举出一个符合题设的具体函数的例子.21.(本小题满分12分)某公司为获更大收益,每年要投入一定资金用于广告促销,经调查,若每年投广告费(百万元),可增加销售额约为(百万元)..(1)若公司将当年的广告费控制在3百万元之内,则应投入多少广告费才能使公司由此获得收益最大?(2)现公司准备共投入3百万元分别用于广告促销和技术改造,经预测,每投入技术改进费百万元,可增加销售额约百万元.请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益=销售额-成本)22.(本小题满分14分)若关于的方程恰有一个实数解,求实数的取值范围.参考答案一、选择题题号123456789101112答案DCABCBABDCAD二、填空题13.;14.y轴;15.和;16.1;三、解答题17.(12′)解:(1)当时,则,∴由,∴,∴(2).∴的取值范围是18(12′)解:(1)为奇函数,∴(2)由(1),任取.∵,,又.∴.∴由定义知在R上为增函数。19.(12′)解:(1)设.由假设..与直线切于点∴.∴.(2)20.(12′)解(1)∴为奇函数(2)先证在R上减任取..(∵)∴∴在R上为减函数..∵∴最大值为6.最小值为.(3)比如21.(12′)解:(1)设投入广告费t百万元,则收益。∴时,.∴应投入2百万元广告费,由此获得收益最大。(2)投入广告费百万元.则收益当时,.∴当投入技术改造2百万元、广告费1百万元时,公司收益最大。22.(14′)解:原方程1°当△=0时满足∴此时合题意.2°当△>0时,即.,显然.∵(当且仅当时,取“=”号,而当,,此时原方程仍有唯一解)当一定是原方程的解故使原方程有唯一解,则必须(∵.且).综上,当,或时,原方程有唯一解.