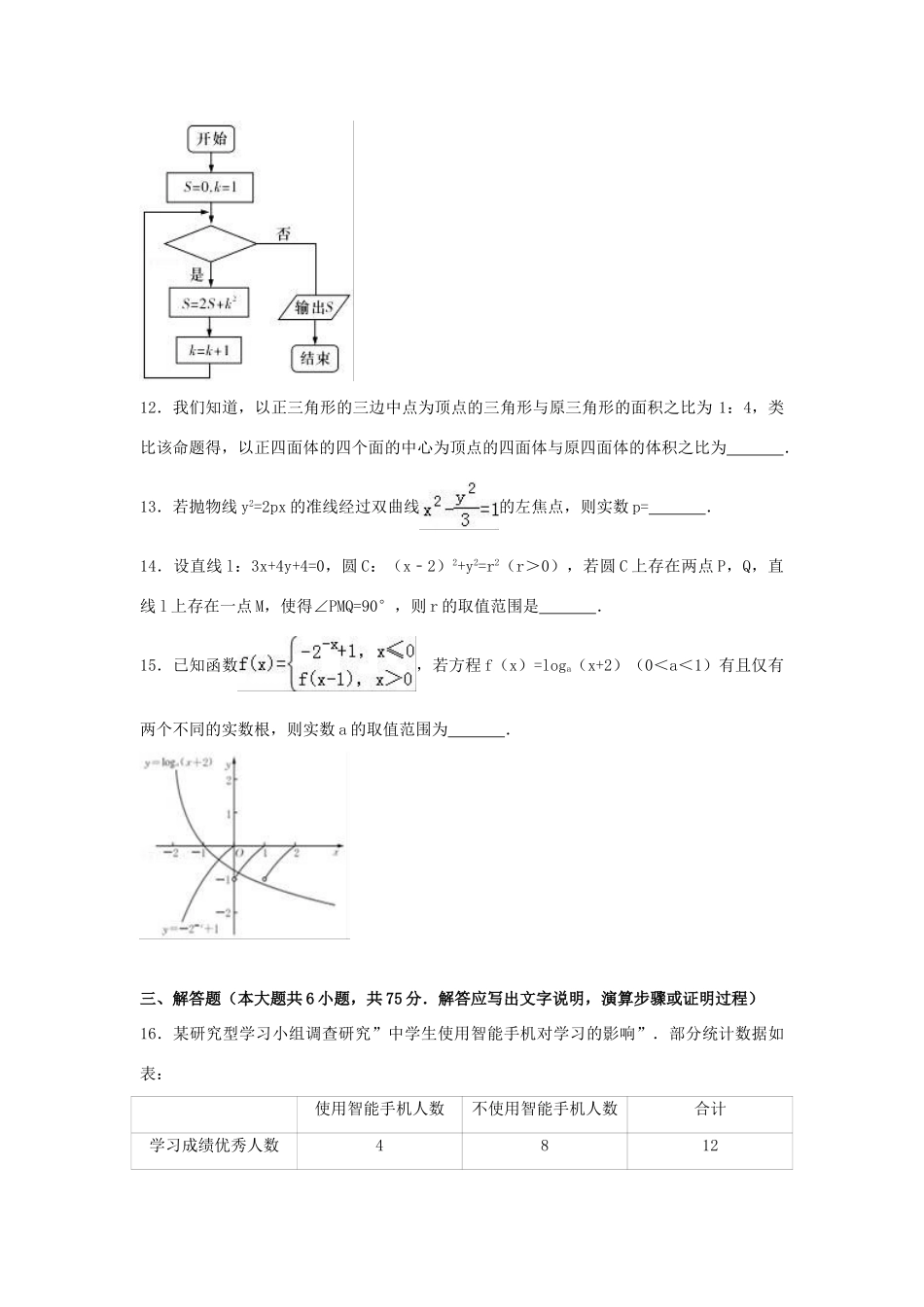
2017年山东省枣庄市高考最后冲刺模拟数学试卷(文科)一、选择题(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个选项是符合题目求的).1.已知集合A={1,2,3},B={x|x2﹣x﹣6=0},则A∩B=()A.{1}B.{2}C.{3}D.{2,3}2.若复数z满足i(z﹣1)=1+i(i虚数单位),则z=()A.2﹣iB.2+iC.1﹣2iD.1+2i3.已知甲、乙两位同学8次数学单元测试的成绩(百分制)可用如图所示的茎叶图表示,且甲同学成绩的平均数比乙同学成绩的平均数小2,则乙同学成绩的方差为()A.B.C.D.4.祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设A、B为两个同高的几何体,p:A、B的体积不相等,q:A、B在等高处的截面积不恒相等,根据祖暅原理可知,p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中,则函数g(x)=cos(2x﹣φ)的图象()A.关于点对称B.关于轴对称C.可由函数f(x)的图象向右平移个单位得到D.可由函数f(x)的图象向左平移个单位得到6.已知向量=(1,),=(3,m),若向量,的夹角为,则实数m=()A.2B.C.0D.﹣7.一个几何体的三视图如图所示,该几何体的体积为()A.24﹣πB.24﹣3πC.D.8.在△ABC中,角A、B、C的对边分别为a,b,c,且b(2sinB+sinA)+(2a+b)sinA=2csinC,则C=()A.B.C.D.9.已知三棱锥P﹣ABC的三条侧棱两两互相垂直,且AB=,BC=,AC=2,则此三棱锥的外接球的体积为()A.πB.πC.πD.π10.已知定义域在R上的函数f(x)满足f(x+1)+f(1﹣x)=2,当x>1时,f(x)=,则关于x的方程f(x)+2a=0没有负实根时实数a的取值范围是()A.(﹣∞,﹣1]∪[,+∞)B.(0,1)C.(﹣1,,)∪(,+∞)D.(﹣2,)∪(,0)二、填空题(本大题共5个小题,每小题5分,共25分).11.阅读如图所示的程序框图,若输出的数据为58,则判断框中应填入的条件为.12.我们知道,以正三角形的三边中点为顶点的三角形与原三角形的面积之比为1:4,类比该命题得,以正四面体的四个面的中心为顶点的四面体与原四面体的体积之比为.13.若抛物线y2=2px的准线经过双曲线的左焦点,则实数p=.14.设直线l:3x+4y+4=0,圆C:(x﹣2)2+y2=r2(r>0),若圆C上存在两点P,Q,直线l上存在一点M,使得∠PMQ=90°,则r的取值范围是.15.已知函数,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为.三、解答题(本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程)16.某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如表:使用智能手机人数不使用智能手机人数合计学习成绩优秀人数4812学习成绩不优秀人数16218合计201030参考数据:P(K2≥k0)0.150.100.050.0250.0100.0050.001k02.0722.7063.8415.0246.6357.87910.828参考公式:,其中n=a+b+c+d(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.17.已知函数f(x)=sin(ωx+φ)+2sin2()﹣1(ω>0,0<φ<π)为奇函数,且相邻两对称轴间的距离为.(1)当时,求f(x)的单调递减区间;(2)将函数y=f(x)的图象向右平移个单位长度,再把横坐标缩小为原来的(纵坐标不变),得到函数y=g(x)的图象,当时,求函数g(x)的值域.18.在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.(Ⅰ)求证:PB∥平面FAC;(Ⅱ)求三棱锥P﹣EAD的体积;(Ⅲ)求证:平面EAD⊥平面FAC.19.已知等比数列{an}的各项均为正数,a1=1,公比为q;等差数列{bn}中,b1=3,且{bn}...