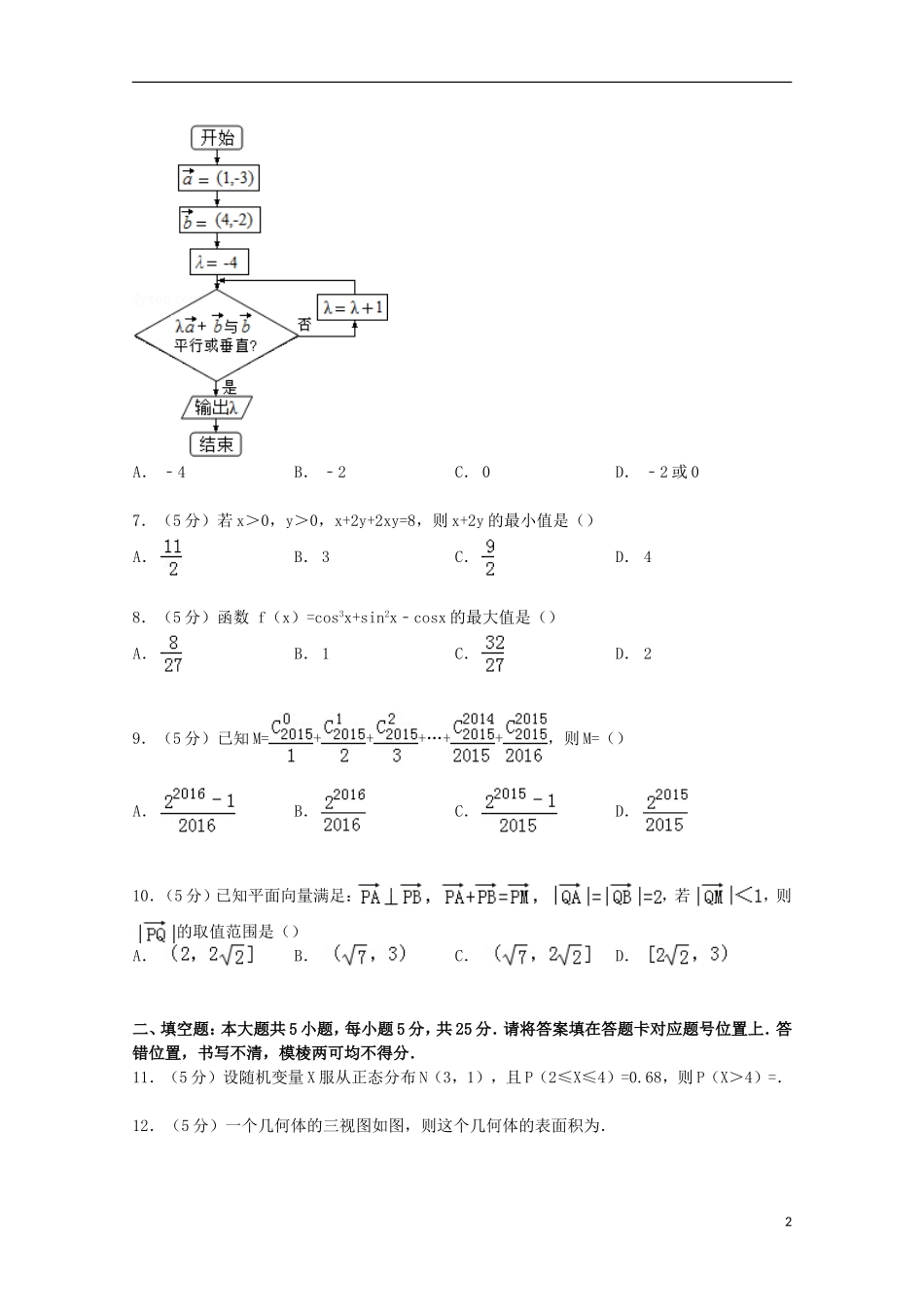
山东省济宁市微山一中2015届高考数学二模试卷(理科)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,有一项是符合题目要求的.1.(5分)设i为虚数单位,则复数=()A.﹣4﹣3iB.﹣4+3iC.4+3iD.4﹣3i2.(5分)为了得到函数y=3cos2x的图象,只需把函数的图象上所有的点()A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位3.(5分)设α,β,γ为平面,m,n为直线,则m⊥β的一个充分条件是()A.α⊥β,α∩β=n,m⊥nB.α∩γ=m,α⊥γ,β⊥γC.α⊥β,β⊥γ,m⊥αD.n⊥α,n⊥β,m⊥α4.(5分)如果等差数列{an}中,a1=﹣11,,则S11=()A.﹣11B.10C.11D.﹣105.(5分)若变量x,y满足约束条件,则z=2x+y的最大值是()A.4B.3C.2D.16.(5分)执行如图的程序框图,则输出的λ是()1A.﹣4B.﹣2C.0D.﹣2或07.(5分)若x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.B.3C.D.48.(5分)函数f(x)=cos3x+sin2x﹣cosx的最大值是()A.B.1C.D.29.(5分)已知M=+++…++,则M=()A.B.C.D.10.(5分)已知平面向量满足:,若,则的取值范围是()A.B.C.D.二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)设随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.68,则P(X>4)=.12.(5分)一个几何体的三视图如图,则这个几何体的表面积为.213.(5分)在正方体的8个顶点,12条棱的中点,6个面的中心及正方体的中心共27个点中,共线的三点组的个数是.14.(5分)已知曲线Γ:ρ=,θ∈R与曲线C:,t∈R相交于A,B两点,又原点O(0,0),则|OA|•|OB|=.15.(5分)在△ABC中,内角A,B,C的所对边分别是a,b,c,有如下下列命题:①若A>B>C,则sinA>sinB>sinC;②若,则△ABC为等边三角形;③若sin2A=sin2B,则△ABC为等腰三角形;④若(1+tanA)(1+tanB)=2,则△ABC为钝角三角形;⑤存在A,B,C,使得tanAtanBtanC<tanA+tanB+tanC成立.其中正确的命题为(写出所有正确命题的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(12分)已知函数f(x)=sin2x+2sinxcosx﹣cos2x,x∈R.求:(Ⅰ)函数f(x)的单调增区间;(Ⅱ)若,求函数f(x)的值域.17.(12分)某校一个研究性学习团队从网上查得,某种植物种子在一定条件下的发芽成功的概率为,于是该学习团队分两个小组进行验证性实验.(Ⅰ)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;(Ⅱ)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则就继续进行下次实验.直到种子发芽成功为止,但实验的次数不超过5次.求这一小组所做的种子发芽实验次数ξ的分布列和期望.318.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.(Ⅰ)证明:直线NC∥平面PAD;(Ⅱ)求平面MNC与底面ABCD所成的锐二面角的余弦值;(Ⅲ)求三棱锥P﹣MNC的体积V.19.(12分)已知函数,(x≥0),又数列{an}中,an>0,a1=2,该数列的前n项和记为Sn,对所有大于1的自然数n都有Sn=f(Sn﹣1).(Ⅰ)求{an}的通项公式;(Ⅱ)记bn=,{bn}其前n项和为Tn,证明:Tn<n+1.20.(13分)已知F1、F2分别是椭圆的左、右焦点,P是此椭圆上的一动点,并且的取值范围是.(Ⅰ)求此椭圆的方程;(Ⅱ)点A是椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限内),又P、Q是椭圆上两点,并且满足,求证:向量共线.21.(14分)设函数f(x)=xlnx.(Ⅰ)求f(x)的极值;(Ⅱ)设g(x)=f(x+1),若对任意的x≥0,都有g(x)≥mx成立,求实数m的取值范围;(Ⅲ)若0<a<b,证明:.山东省济宁市微山一中2015届高考数学二模试卷(理科)4参考答案与试题解析一、选择题:本大题共10小题,每小题5分,满分50分.在...