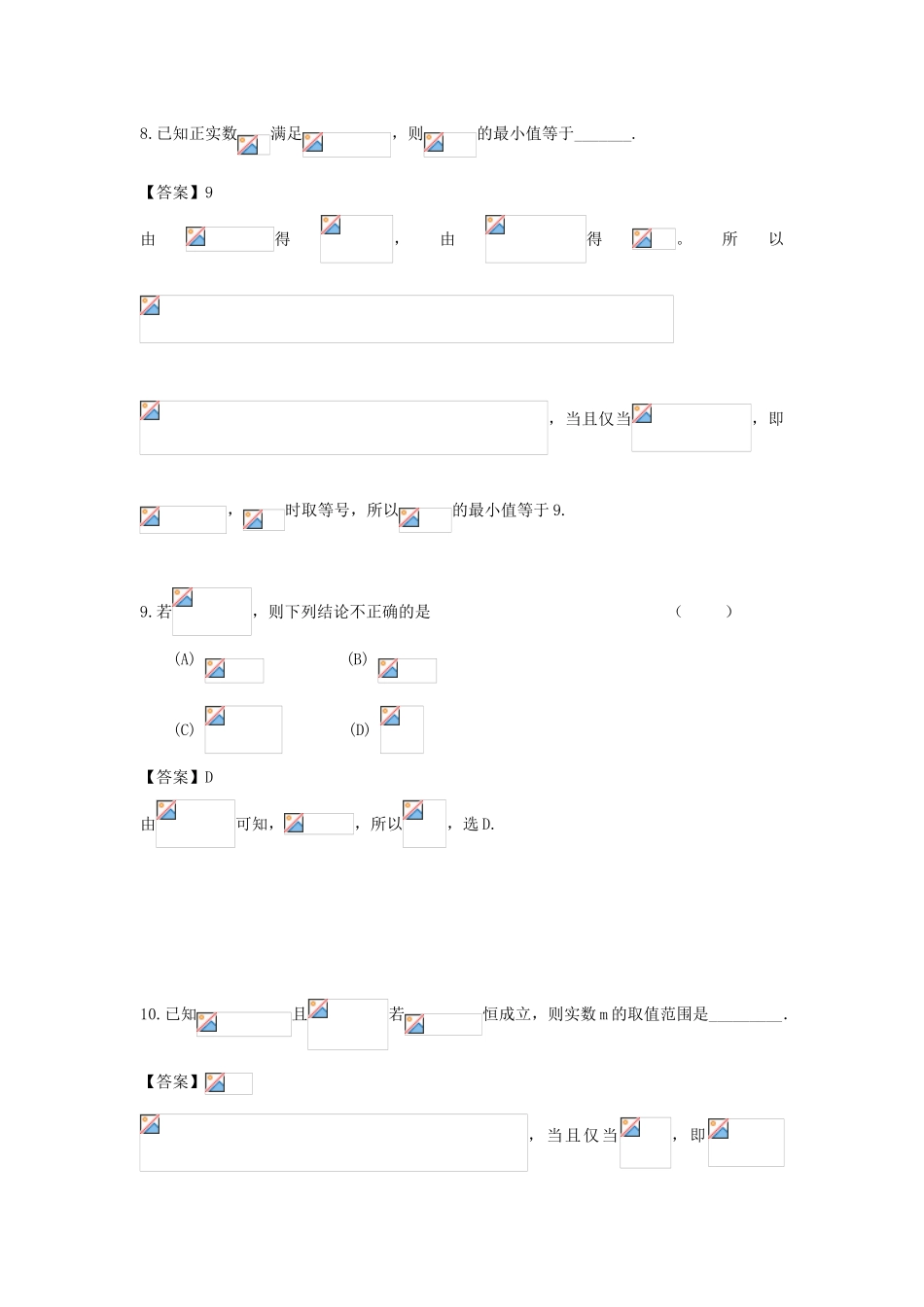
不等式1.均为正实数,且,,,则()A.B.C.D.【答案】A因为均为正实数,所以,即,所以。,因为,即,所以,即。,因为,所以,即,所以,选A.2.由得,即,所以不等式的解集为。已知,则的最小值为▲.【答案】2由得且,即。所以,所以的最小值为2.3.不等式的解为.【答案】由行列式的定义可知不等式为,整理得,解得,或(舍去),所以。4.若实常数,则不等式的解集为.【答案】因为,得,解得,即不等式的解集为。5.已知,关于的不等式的解集是.【答案】原不等式等价为,即,因为,所以不等式等价为,所以,即原不等式的解集为。6.已知不等式对任意恒成立,则实数的取值范围是.【答案】或当时,,此时不等式成立,所以只考虑时,若,则不等式等价为,此时。若,则不等式等价为,即,因为,所以,所以。所以实数的取值范围是或。7.若对于任意的不等式恒成立,则实数的取值范围为_______.【答案】,所以要使恒成立,则,即实数的取值范围为。8.已知正实数满足,则的最小值等于_______.【答案】9由得,由得。所以,当且仅当,即,时取等号,所以的最小值等于9.9.若,则下列结论不正确的是()(A)(B)(C)(D)【答案】D由可知,,所以,选D.10.已知且若恒成立,则实数m的取值范围是_________.【答案】,当且仅当,即时,取等号,所以的最小值为4,所以要使恒成立,所以。11.不等式的解集是_________________.【答案】由得,即,所以解得,所以不等式的解集为。12.如图所示,是一个矩形花坛,其中AB=6米,AD=4米.现将矩形花坛扩建成一个更大的矩形花园,要求:B在上,D在上,对角线过C点,且矩形的面积小于150平方米.(1)设长为米,矩形的面积为平方米,试用解+析+式将表示成的函数,并写出该函数的定义域;(2)当的长度是多少时,矩形的面积最小?并求最小面积.【答案】解:(1)由△NDC∽△NAM,可得,∴,即,……………………3分故,………………………5分由且,可得,解得,故所求函数的解+析+式为,定义域为.…………………………………8分(2)令,则由,可得,故…………………………10分,…………………………12分当且仅当,即时.又,故当时,取最小值96.故当的长为时,矩形的面积最小,最小面积为(平方米)…………14分13.已知函数,其中常数a>0.(1)当a=4时,证明函数f(x)在上是减函数;(2)求函数f(x)的最小值.【答案】(1)当时,,…………………………………………1分任取00,即f(x1)>f(x2)………………………………………5分所以函数f(x)在上是减函数;………………………………………………………6分(2),……………………………………………………7分当且仅当时等号成立,…………………………………………………………8分当,即时,的最小值为,………………………10分当,即时,在上单调递减,…………………………………11分所以当时,取得最小值为,………………………………………………13分综上所述:………………………………………14分