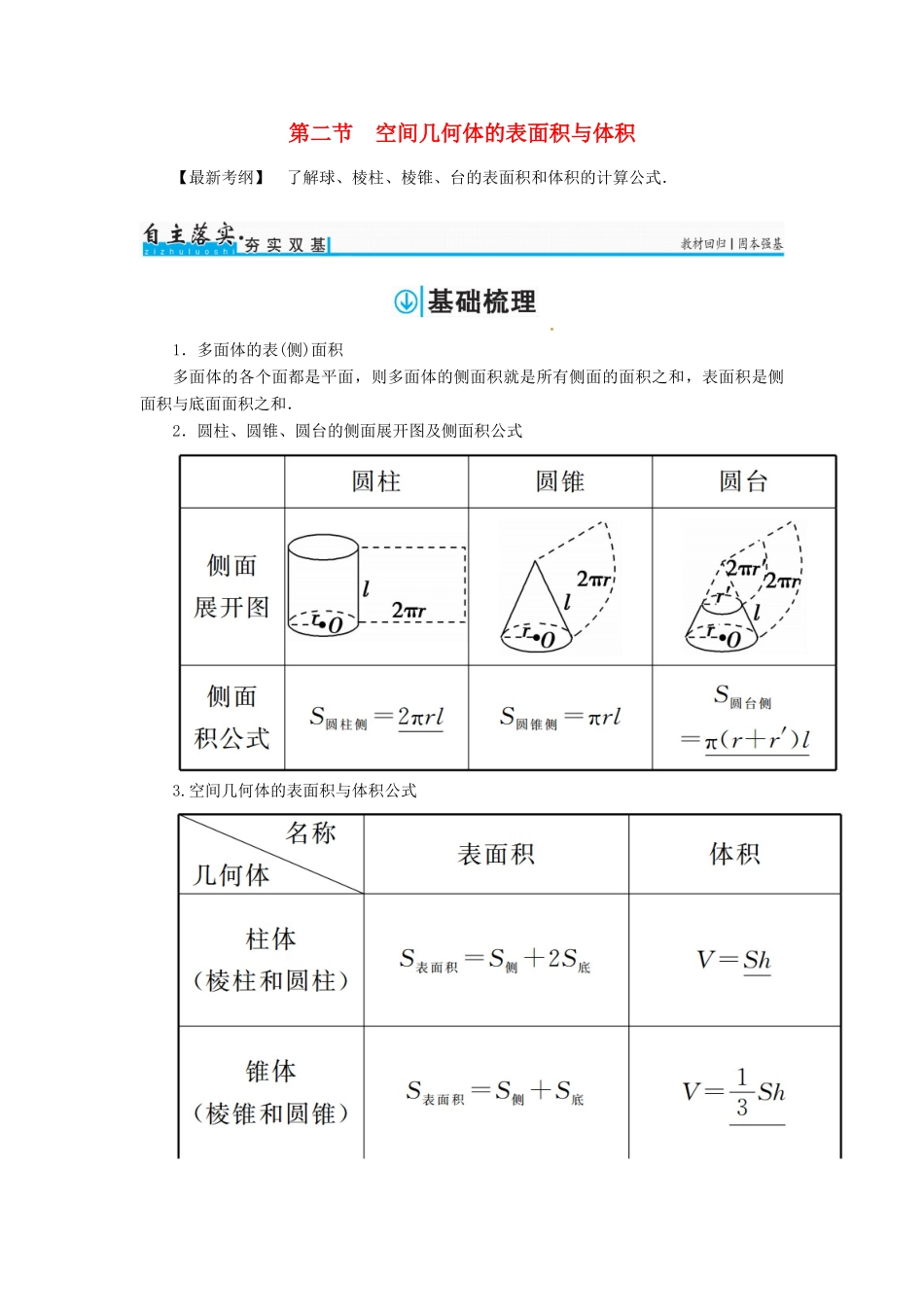
第二节空间几何体的表面积与体积【最新考纲】了解球、棱柱、棱锥、台的表面积和体积的计算公式.1.多面体的表(侧)面积多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式3.空间几何体的表面积与体积公式1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)锥体的体积等于底面面积与高之积.()(2)球的体积之比等于半径比的平方.()(3)台体的体积可转化为两个锥体的体积之差.()(4)已知球O的半径R,其内接正方体的边长为a,则R=a.()答案:(1)×(2)×(3)√(4)√2.已知圆锥的表面积为am2,且它的侧面展开图是一个半圆,则这个圆锥的底面直径是()A.B.C.D.解析:设圆锥的底面半径为r,母线长为l,由题意知2πr=πl,∴l=2r,则圆锥的表面积S表=πr2+2πr2=a,∴r2=,直径2r=.答案:C3.(2015·新课标全国Ⅰ卷)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛解析:设米堆的底面半径为r尺,则r=8,所以r=.所以米堆的体积为V=×π·r2·5=··5≈(立方尺).故堆放的米约有÷1.62≈22(斛).答案:B4.已知一个正方体的所有顶点在一个球面上.若球的体积为,则正方体的棱长为________.解析:设球的半径为R,则πR3=.∴R=,又2R=a,得a=.答案:5.(2016·邯郸质检)某几何体的三视图如图所示,则该几何体的体积为________.解析:由三视图知该几何体为直四棱柱,其底面为等腰梯形,上底长为2,下底长为8,高为4,故面积为S==20.又棱柱的高为10,所以体积V=Sh=20×10=200.答案:200一种思想——转化与化归思想计算旋转体的侧面积时,一般是将侧面展开化为平面图形,“化曲为直”来解决,因此要熟悉常见旋转体的侧面展开图的形状及平面图形面积的求法.两种方法——割补法与等积法1.割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.2.等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.两个注意点——求空间几何体的表面积应注意两点1.求组合体的表面积时,要注意各几何体重叠部分的处理.2.底面是梯形的四棱柱侧放时,容易和四棱台混淆,在识别时要紧扣定义,以防出错.A级基础巩固一、选择题1.(2014·课标全国Ⅱ卷)正三棱柱ABCA1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥AB1DC1的体积为()A.3B.C.1D.解析:因为B1C1∥BD,所以BD∥平面AB1C1,∴点B和D到面AB1C1的距离相等.所以VAB1DC1=VDAB1C1=VBAB1C1=VC1ABB1=××2×()2=1.答案:C2.(2014·湖北卷)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈L2h相当于将圆锥体积公式中的π近似取为()A.B.C.D.解析:设圆锥的底面圆半径为r,则圆锥的底面圆周长L=2πr,所以圆锥底面圆的半径r=,则圆锥的体积为V=Sh=πr2h=π·h=L2h.又V≈L2h,所以L2h≈L2h,解得π≈.答案:B3.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是()A.2B.C.D.3解析:由三视图知,该几何体是四棱锥,底面是直角梯形,且S底=(1+2)×2=3.∴V=x·3=3,解得x=3.答案:D4.正四棱锥的顶点都在同...