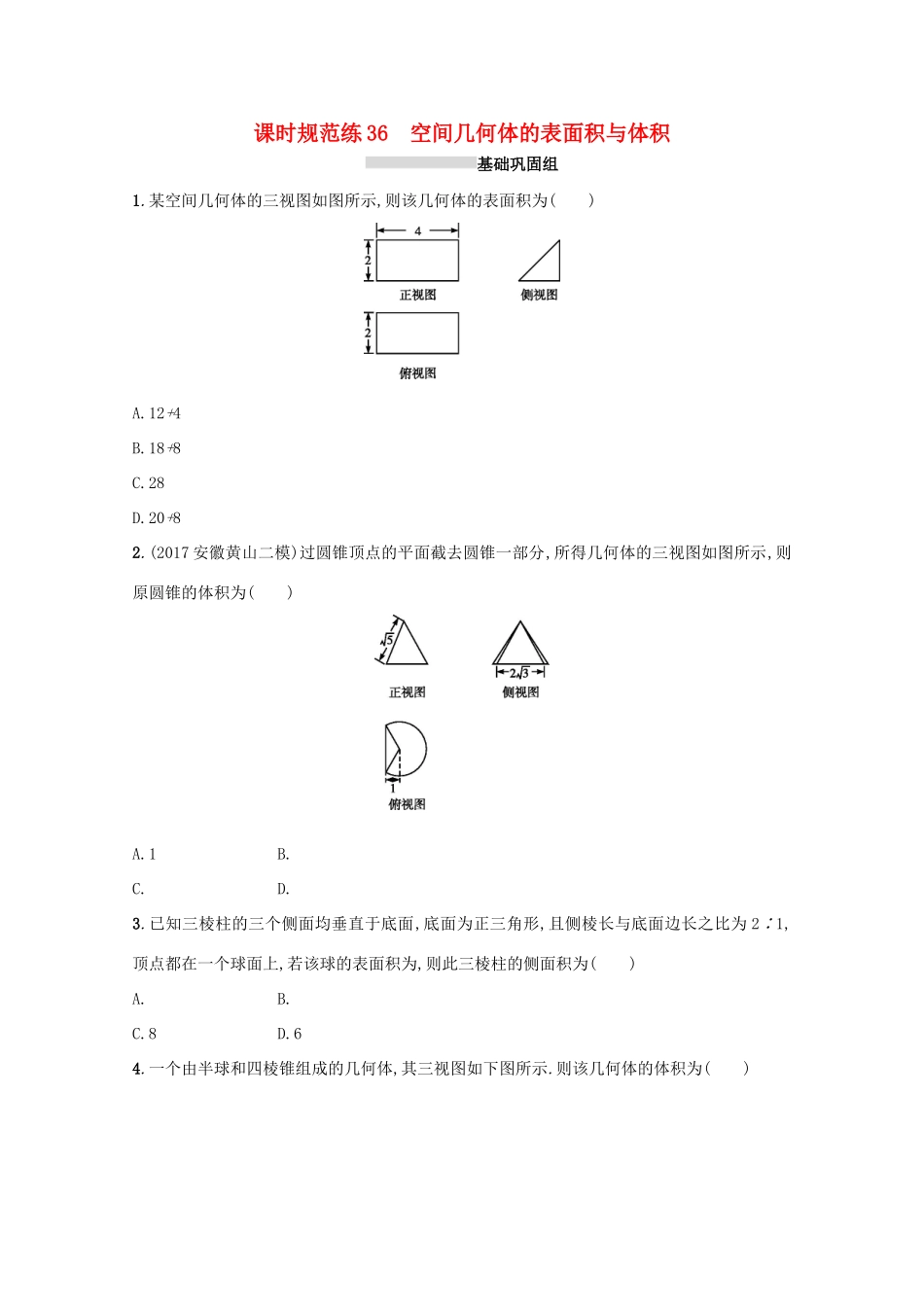
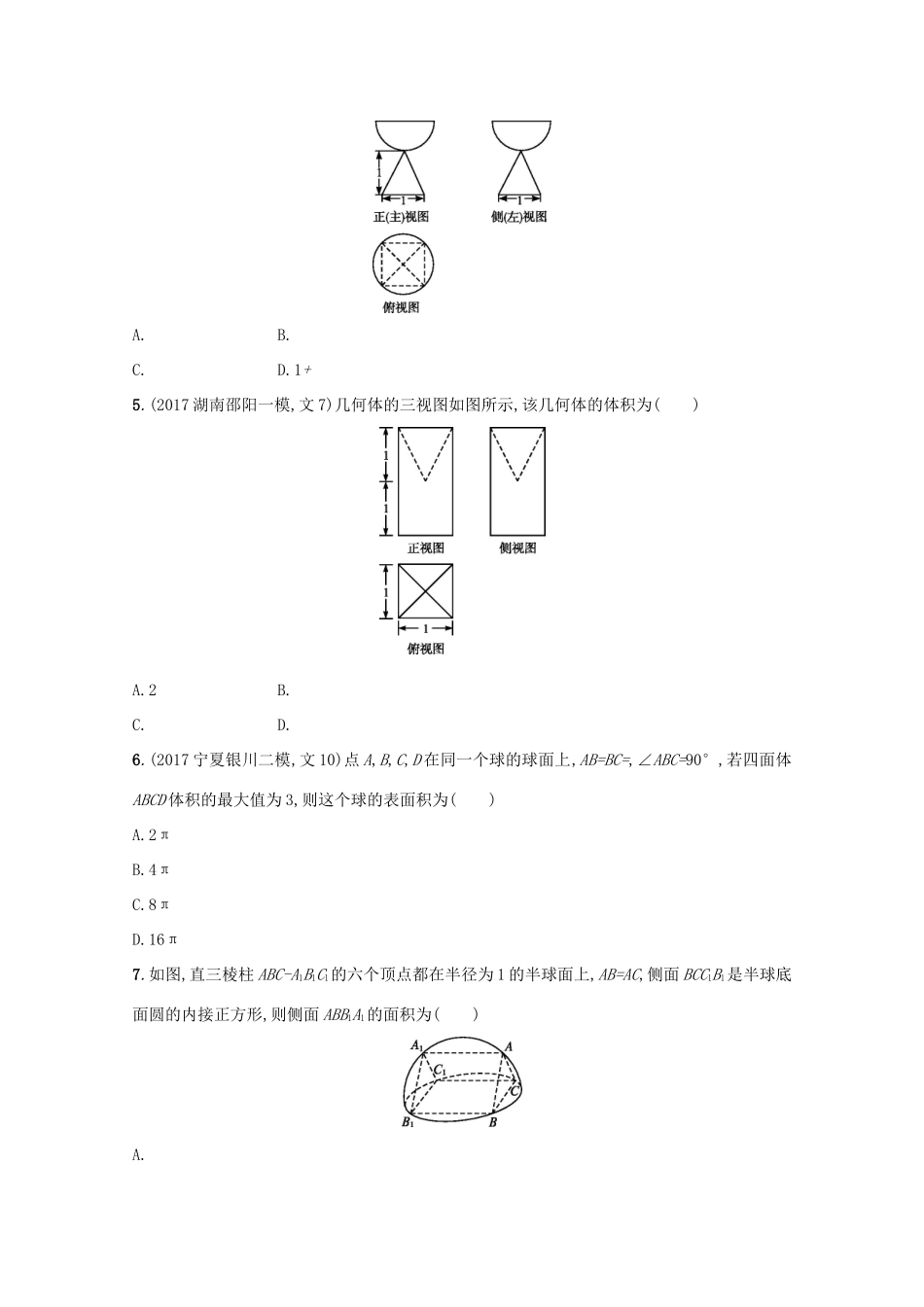
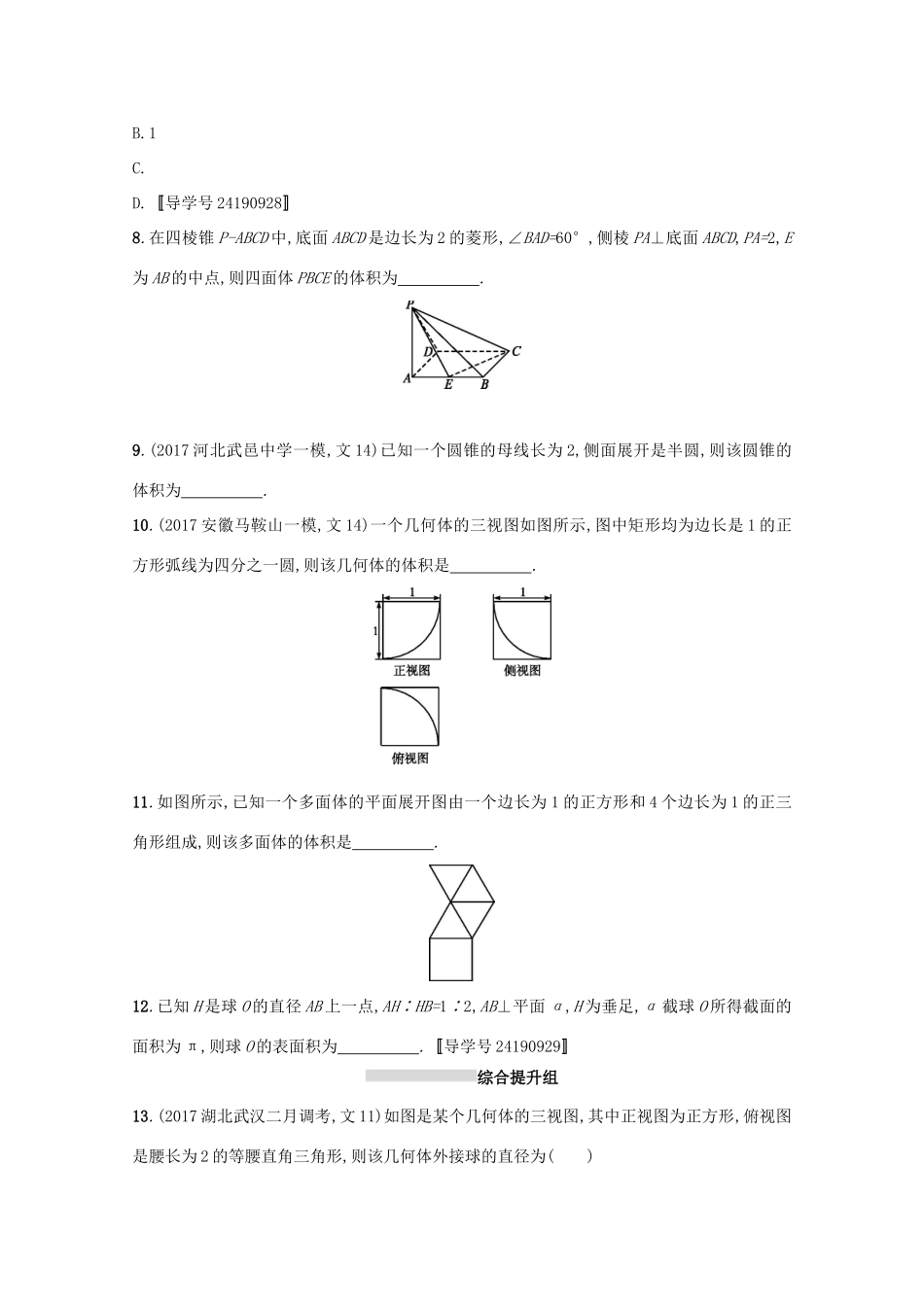
课时规范练36空间几何体的表面积与体积基础巩固组1.某空间几何体的三视图如图所示,则该几何体的表面积为()A.12+4B.18+8C.28D.20+82.(2017安徽黄山二模)过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如图所示,则原圆锥的体积为()A.1B.C.D.3.已知三棱柱的三个侧面均垂直于底面,底面为正三角形,且侧棱长与底面边长之比为2∶1,顶点都在一个球面上,若该球的表面积为,则此三棱柱的侧面积为()A.B.C.8D.64.一个由半球和四棱锥组成的几何体,其三视图如下图所示.则该几何体的体积为()A.B.C.D.1+5.(2017湖南邵阳一模,文7)几何体的三视图如图所示,该几何体的体积为()A.2B.C.D.6.(2017宁夏银川二模,文10)点A,B,C,D在同一个球的球面上,AB=BC=,∠ABC=90°,若四面体ABCD体积的最大值为3,则这个球的表面积为()A.2πB.4πC.8πD.16π7.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为()A.B.1C.D.导学号〚24190928〛8.在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,PA=2,E为AB的中点,则四面体PBCE的体积为.9.(2017河北武邑中学一模,文14)已知一个圆锥的母线长为2,侧面展开是半圆,则该圆锥的体积为.10.(2017安徽马鞍山一模,文14)一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是.11.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是.12.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为.导学号〚24190929〛综合提升组13.(2017湖北武汉二月调考,文11)如图是某个几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体外接球的直径为()A.2B.2C.D.214.(2017河南南阳一模,文11)一个四面体的顶点都在球面上,它的正视图、侧视图、俯视图都是下图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是()A.πB.3πC.4πD.6π15.已知正四棱锥O-ABCD的体积为,底面边长为,则以O为球心,OA为半径的球的表面积为.16.(2017陕西咸阳二模,文16)已知三棱锥的所有棱长均为,则该三棱锥的外接球的直径为.创新应用组17.已知三棱锥S-ABC的所有顶点都在球O的球面上,且SC⊥平面ABC,SC=AB=AC=1,∠BAC=120°,则球O的表面积为.18.(2017福建宁德一模,文14)已知正三棱柱ABC-A1B1C1的顶点都在同一个球面上,且该正三棱柱的体积为,△ABC周长为3,则这个球的表面积为.导学号〚24190930〛课时规范练36空间几何体的表面积与体积1.D由三视图可知该几何体是底面为等腰直角三角形的直三棱柱,如图.则该几何体的表面积为S=2××2×2+4×2×2+2×4=20+8,故选D.2.D由三视图可得底面圆的半径为=2,圆锥的高为=2,∴原圆锥的体积为π×22×2=,故选D.3.D如图,根据球的表面积可得球的半径为r=,设三棱柱的底面边长为x,则=x2+,解得x=1,故该三棱柱的侧面积为3×1×2=6.4.C由三视图可知,上面是半径为的半球,体积V1=π×,下面是底面积为1,高为1的四棱锥,体积V2=×1×1=,所以该几何体的体积V=V1+V2=.故选C.5.D由已知中的三视图,可知该几何体是一个长方体,切去了一个边长为1,高也是1的正四棱锥(如图),长方体ABCD-A'B'C'D'切去正四棱锥S-ABCD.长方体的体积为V长方体=1×1×2=2,正四棱锥的体积为V正四棱锥=×1×1×1=,故该几何体的体积V=2-.故选D.6.D由题意,知S△ABC=3,设△ABC所在球的小圆的圆心为Q,则Q为AC的中点,当DQ与面ABC垂直时,四面体ABCD的最大体积为S△ABC·DQ=3,∴DQ=3,如图,设球心为O,半径为R,则在Rt△AQO中,OA2=AQ2+OQ2,即R2=()2+(3-R)2,∴R=2,则这个球的表面积为S=4π×22=16π.故选D.7.C由题意知,球心在侧面BCC1B1的中心O上,BC为△ABC所在圆面的直径,所以∠BAC=90°,△ABC的外接圆圆心N是BC的中点,同理△A1B1C1的外心M是B1C1的中点.设正方形BCC1B1的边长为x,在Rt△OMC1中,OM=,MC1=,OC1=R=1(R为球的半径),所以=1,即x=,则AB=AC=1.所以侧面ABB1A1的面积S=×1=.8.显然PA⊥面BCE,底面BCE的面积为×1×2×sin120°=,所以VP-BCE=×2×.9.π...