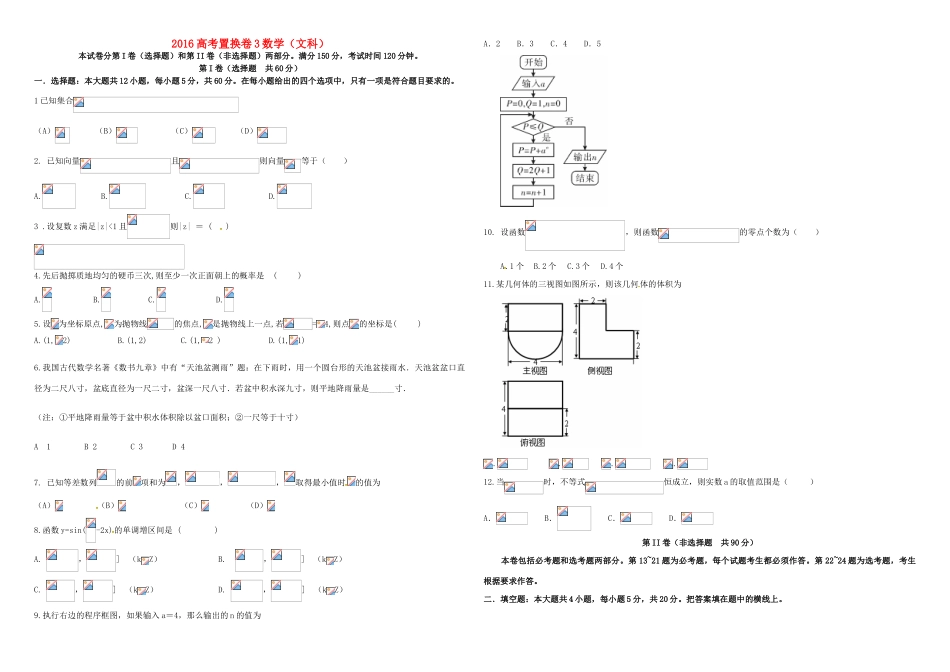
2016高考置换卷3数学(文科)本试卷分第I卷(选择题)和第II卷(非选择题)两部分。满分150分,考试时间120分钟。第I卷(选择题共60分)一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1已知集合(A)(B)(C)(D)2.已知向量且则向量等于()A.B.C.D.3.设复数z满足|z|<1且则|z|=()4.先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是()A.B.C.D.5.设为坐标原点,为抛物线的焦点,是抛物线上一点,若=4,则点的坐标是()A.(1,2)B.(1,2)C.(1,2)D.(1,1)6.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是______寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)A1B2C3D47.已知等差数列的前项和为,,,取得最小值时的值为(A)(B)(C)(D)8.函数y=sin(-2x)的单调增区间是()A.,](kZ)B.,](kZ)C.,](kZ)D.,](kZ)9.执行右边的程序框图,如果输入a=4,那么输出的n的值为A.2B.3C.4D.510.设函数,则函数的零点个数为()A.1个B.2个C.3个D.4个11.某几何体的三视图如图所示,则该几何体的体积为....12.当时,不等式恒成立,则实数a的取值范围是()A.B.C.D.第II卷(非选择题共90分)本卷包括必考题和选考题两部分。第13~21题为必考题,每个试题考生都必须作答。第22~24题为选考题,考生根据要求作答。二.填空题:本大题共4小题,每小题5分,共20分。把答案填在题中的横线上。13.已知数列的前n项和,对于任意的都成立,则S10=。14.已知函数,则函数的图象在点处的切线方程是.15.已知满足,则的取值范围是.16.已知双曲线的一条渐近线方程是,它的一个焦点与抛物线的焦点相同,则双曲线的方程为.三.解答题:本大题共6小题,前5题每题12分,选考题10分,共70分,解答应写出必要的文字说明、证明过程或演算步骤。17.已知的内角、、的对边分别为、、,,且。(1)求角;(2)若向量与共线,求、的值.18.在几何体ABCDE中,∠BAC=,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1。(I)设平面ABE与平面ACD的交线为直线,求证:∥平面BCDE;(II)设F是BC的中点,求证:平面AFD⊥平面AFE;(III)求几何体ABCDE的体积。19.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与医院抄录1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下图资料:日期1月10日2月10日3月10日4月10日5月10日6月10日昼夜温差(℃)1011131286就诊人数222529261612(个)该兴趣小组的研究方案是先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的两组数据检验。(1)求选取的两组数据恰好相邻的概率;(2)若选取的是1月与6月的两组数据,请据2~5月份的数据,求出关于的线性回归方程;(3)若线性回归方程得出的估计数据与所选出的检验数据的误差不超过2人,则认为得到的线性回归方程是理想的。试问该兴趣小组得到的线性回归方程是否理想?20.已知抛物线的顶点是椭圆的中心,焦点与该椭圆的右焦点重合(1)求抛物线的方程(2)已知动直线过点,交抛物线于两点,坐标原点O为中点,求证;(3)是否存在垂直于x轴的直线m被以为直径的圆所截得的弦长恒为定值?如果存在,求出m的方程;如果不存在,说明理由。21.已知函数在处存在极值。(1)求实数的值;(2)函数的图像上存在两点A,B使得是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在轴上,求实数的取值范围;(3)当时,讨论关于的方程的实根个数。请考生在22~24三题中任选一题作答,如果多做,则按所做的第一题记分。22.选修4-1:几何证明选讲如图,的角平分线的延长线交它的外接圆于点(1)证明:∽△;(2)若的面积,求的大小.ABCDEF23.选修4—4:坐标系与参数方程在极坐标系中,圆C的圆心坐标为,半径为2.以极点为原点,极轴为的正半轴,取相同的长度单位建立平面直角坐标系,直线的参数方程为(为参数)(1)求圆C的极坐标方程;(2)设与圆C的交点为...