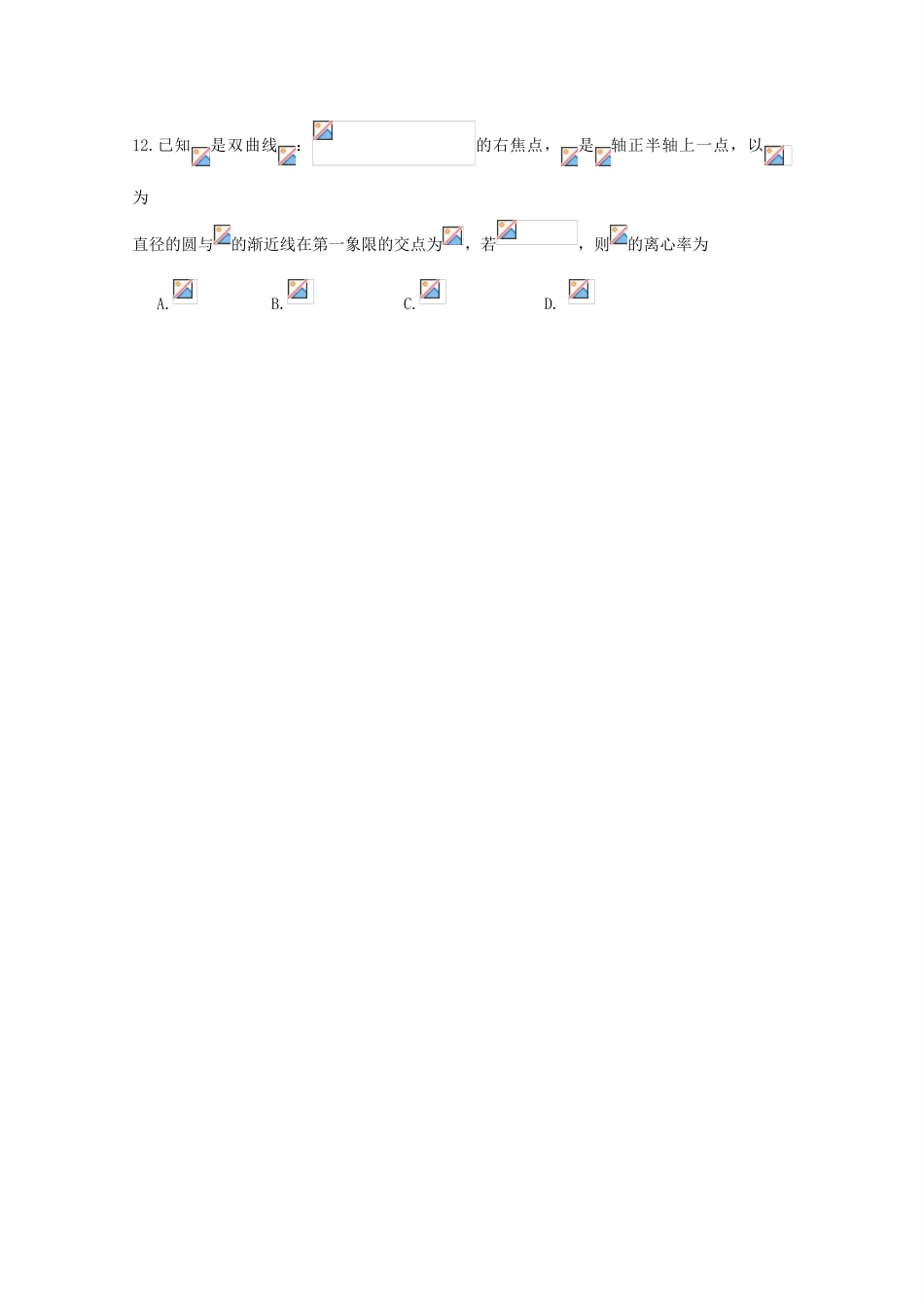
四川省成都市龙泉驿区2018届高三数学9月月考试题文本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题纸上,考生要认真核对答题纸上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦净后,再选涂其他答案标号。第Ⅱ卷用黑色墨水签字笔在答题纸上书写作答,在试题卷上作答,答案无效。第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.记集合,则=A.B.C.D.2.若复数为虚数单位)是纯虚数,则实数的值为A.B.C.D.3.等差数列{an}中,a3=5,a4+a8=22,则{an}的前8项和为A.32B.64C.108D.1284.已知,是两条不同的直线,,是两个不同的平面,给出下列四个命题,错误的命题是A.若,,,则B.若,,,则C.若,,,则D.若,,则5.设,函数,若,则等于A.8B.4C.2D.16.已知函数,若,则实数的取值范围A.B.C.D.7.如图,等腰梯形中,且,,则以、为焦点,且过点的双曲线的离心率A.B.C.D.8.已知双曲线的一条渐近线与直线垂直,则该双曲线的焦距为A.B.2C.D.9.甲、乙两名选手参加歌手大赛时,5名评委的打分用茎叶图表示如图,分别表示甲、乙选手分数的中位数,分别表示甲、乙选手分数的标准差,则A.,B.,C.,D.,10.若执行如图所示的框图,则输出的数S等于A.B.1C.D.11.已知方程在上有三个不等的实根,则实数的取值范围是甲乙876754180293412.已知是双曲线:的右焦点,是轴正半轴上一点,以为直径的圆与的渐近线在第一象限的交点为,若,则的离心率为A.B.C.D.第Ⅱ卷非选择题(共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~23题为选考题,考生根据要求作答.二.填空题(本大题共4小题,每小题5分,共20分)13.已知复数,则复数的虚部是.14.设,将函数的图象向右平移个单位后与原图像重合,则的最小值是.15.已知直线l:x-y=1与圆M:x2+y2-2x+2y-1=0相交于A,C两点,点B,D分别在圆M上运动,且位于直线AC两侧,则四边形ABCD面积的最大值为_________.16.设集合由满足下列两个条件的数列构成:①②存在实数,使.(为正整数).在以下数列(1);(2);(3);(4)中属于集合W的数列编号为_______三、解答题:本大题共70分.解答应写出文字说明,证明过程或演算步骤.17.(本题满分12分)在△中,角A、B、C所对的边分别是,且=2,.(Ⅰ)b=3,求的值.(Ⅱ)若△的面积=3,求b,c的值.成绩(分)频率组距y0.0100.040x0.0161009080706050O18.(本题满分12分)为选拔选手参加“汉字听写大会”,某中学举行了一次“汉字听写竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为)进行统计.按照,,,,的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在,的数据).(Ⅰ)求样本容量和频率分布直方图中的、的值;(Ⅱ)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“汉字听写大会”,求所抽取的2名学生中至少有一人得分在内的概率.19.(本题满分12分)如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.(Ⅰ)求证:AC⊥SD;(Ⅱ)若SD⊥平面PAC,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.51234567867893420.(本题满分12分)已知椭圆的离心率为,联接椭圆四个顶点的四边形面积为.(1)求椭圆的方程;(2)是椭圆的左右顶点,是椭圆上任意一点,椭圆在点处的切线与过且与轴垂直的直线分别交于两点,直线交于,是否存在实数,使恒成立,并说明理由.21.(本题满分12分)已知函数.(1)当时,求的图像在处的切线方程;(2)若函数在上有两个零点,求实数的取值范围.请考生在第22、23中任选一题作答,如果多做,则按所做的第一题计...