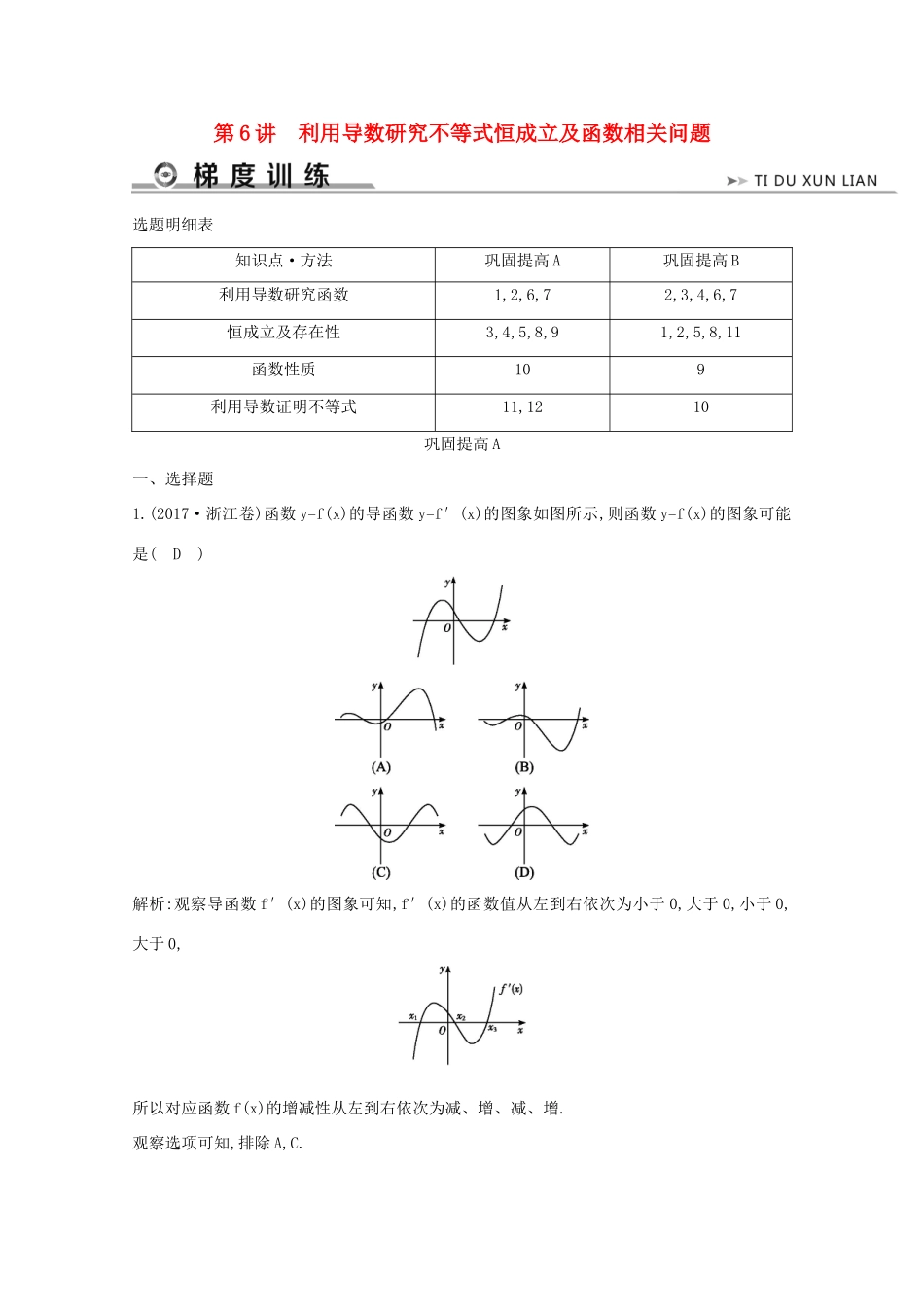
第6讲利用导数研究不等式恒成立及函数相关问题选题明细表知识点·方法巩固提高A巩固提高B利用导数研究函数1,2,6,72,3,4,6,7恒成立及存在性3,4,5,8,91,2,5,8,11函数性质109利用导数证明不等式11,1210巩固提高A一、选择题1.(2017·浙江卷)函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是(D)解析:观察导函数f′(x)的图象可知,f′(x)的函数值从左到右依次为小于0,大于0,小于0,大于0,所以对应函数f(x)的增减性从左到右依次为减、增、减、增.观察选项可知,排除A,C.如图所示,f′(x)有3个零点,从左到右依次设为x1,x2,x3,且x1,x3是极小值点,x2是极大值点,且x2>0,故选项D正确.故选D.2.直线x=t分别与函数f(x)=ex+1的图象及g(x)=2x-1的图象相交于点A和点B,则AB的最小值为(C)(A)2(B)3(C)4-2ln2(D)3-2ln2解析:由题意得,AB=|ex+1-(2x-1)|=|ex-2x+2|,令h(x)=ex-2x+2,则h′(x)=ex-2,所以h(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,所以h(x)min=h(ln2)=4-2ln2>0,即AB的最小值是4-2ln2.故选C.3.已知函数f(x)=x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是(A)(A)[,+∞)(B)(,+∞)(C)(-∞,2](D)(-∞,2)解析:由题x3-2x2+3m+5≥0在[0,+∞)上恒成立,令g(x)=x3-2x2+3m+5,由g′(x)=x2-4x>0得x>4,由g′(x)≤0得0≤x≤4,所以g(x)min=g(4)=-32+3m+5≥0,得m≥,故选A.4.已知e是自然对数的底数,若函数f(x)=ex-x+a的图象始终在x轴上方,则实数a的取值范围是(C)(A)(-∞,-1)∪(0,1)(B)(-1,0)∪(1,+∞)(C)(-1,+∞)(D)(0,1)∪(1,+∞)解析:由题ex-x+a>0恒成立,f′(x)=ex-1,所以f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,所以f(x)min=f(0)=1-0+a>0,得a>-1.5.已知函数f(x)=x+ex-a,g(x)=ln(x+2)-4ea-x,其中e为自然对数的底数,若存在实数x0使f(x0)-g(x0)=3成立,则实数a的值为(A)(A)-ln2-1(B)ln2-1(C)-ln2(D)ln2解析:由题存在x0,使x0+-ln(x0+2)+4=3,即+=ln(x0+2)-x0+3,令y1=+,y2=ln(x0+2)-x0+3,y1≥4,当且仅当x0=a+ln2时等号成立,y′2=-1=-,y2=ln(x0+2)-x0+3在(-2,-1)上单调递增,在(-1,+∞)上单调递减,所以y2的最大值为4.所以当a+ln2=-1,即a=-ln2-1时等式成立,故选A.6.若点P是曲线y=x2-2lnx上任意一点,则点P到直线y=x-的距离的最小值为(C)(A)(B)(C)(D)解析:由题意作图如图,当点P是曲线的切线中与直线y=x-平行的直线的切点时,距离最小.曲线y=x2-2lnx,令y′=3x-=1,解得x=1,故点P的坐标为(1,),故点P到直线y=x-的距离的最小值为=,故选C.二、填空题7.若x=1是函数f(x)=x3+的一个极值点,则实数a=.解析:f′(x)=3x2-,f(1)=3-a=0,得a=3.经检验,符合题意.答案:38.设函数f(x)=ax3-3x+1(x∈R),若对于任意x∈[-1,1],都有f(x)≥0成立,则实数a的值为.解析:当x=0时,a∈R,当x∈(0,1]时,a≥,令g(x)=,g′(x)==,g(x)在(0,)上单调递增,在(,1]上单调递减,g(x)max=g()==4,所以a≥4,当x∈[-1,0)时,a≤,g(x)=为增函数,所以g(x)min=4,所以a≤4.综上,a=4.答案:49.已知函数f(x)=x-,g(x)=x2-2ax+4,若对于任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是.解析:f′(x)=1+>0,所以f(x)在[0,1]上为增函数,f(x1)min=f(0)=-1,g′(x)=2x-2a=2(x-a),在(a,+∞)上g(x)单调递增,在(-∞,a)上,g(x)单调递减,或或得a≥.答案:[,+∞)10.函数y=f(x)在其定义域(-,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为.解析:由f′(x)≤0时,f(x)单调递减.由函数图象可知当x∈[-,1]∪[2,3)时,f(x)单调递减,所以f′(x)≤0的解集为[-,1]∪[2,3).答案:[-,1]∪[2,3)三、解答题11.(2017·全国Ⅲ卷)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤--2.(1)解:f(x)的定义域为(0,+∞),f′(x)=+2ax+2a+1=.若a≥0,因为x∈(0,+∞)时,f′(x)>0,故f(x)在(0,+∞)上单调递增.若a<0,因为x∈(0,-)时,f′(x)>0;当x∈(-,+∞)时,f′(x)<0,故f(x)在(0,-)上单调递增,在(-,+∞)上单调递减.(2)证明:由(1)知,当a<0时,f(x)在x=-处取得最大值,最大值为f(-)=ln(-)-1-,所以f(x)≤--2等价于ln(-)-1-≤--2,即ln(-)++1≤0,设g(x)=lnx-x+1,则g′(x)=-1.当x∈(0,1)时,g′(x)>0;当x∈(1,+∞)时,g′(x...