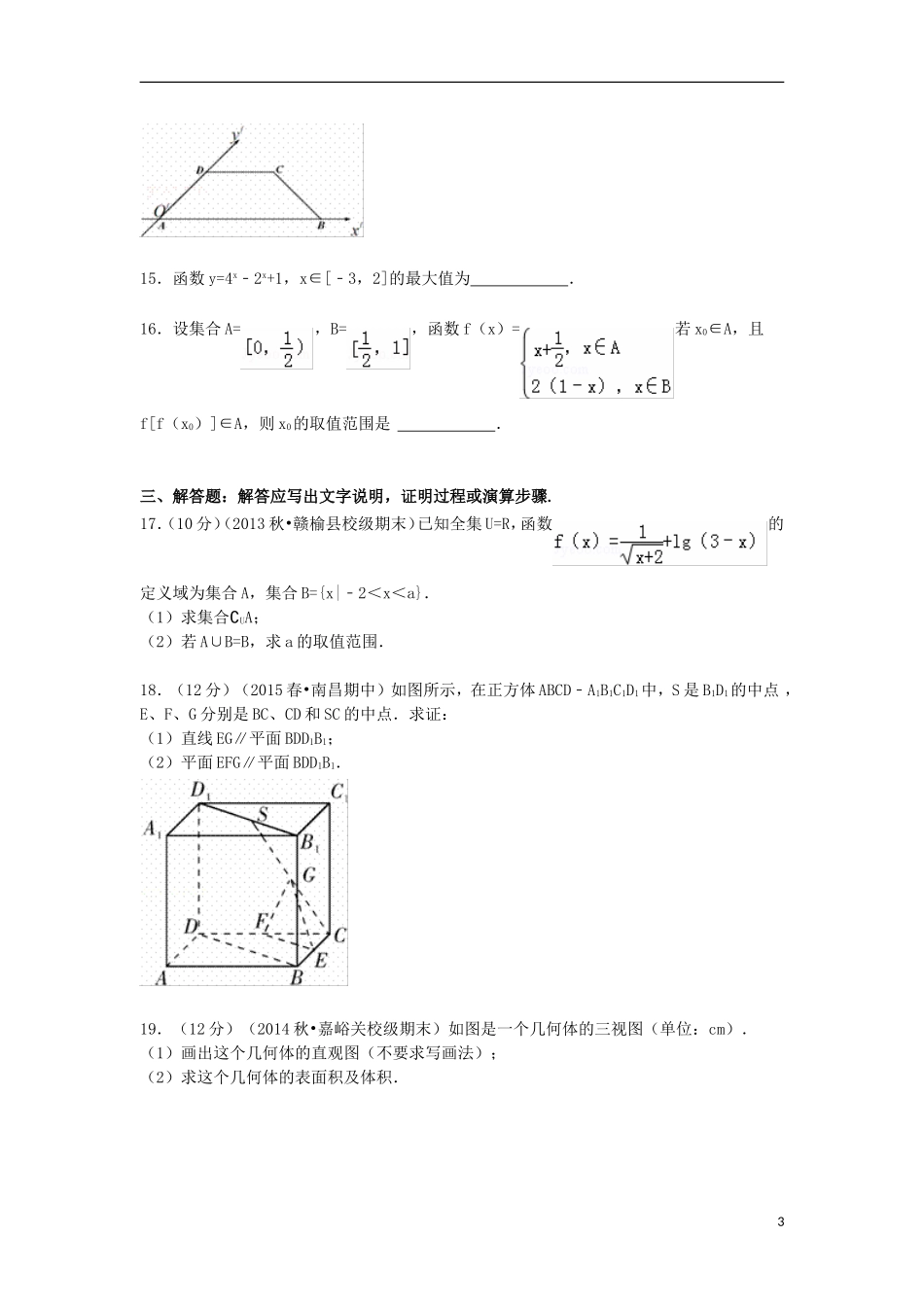
2015-2016学年湖南省株洲二中高一(上)12月月考数学试卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U={1,2,3,4,5,6},A={1,2,5},B={2,3,4},则A∩(∁UB)=()A.{2,6}B.{1,5}C.{1,6}D.{5,6}2.=()A.9B.10C.11D.123.l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面4.设则a,b,c的大小关系是()A.c>b>aB.c>a>bC.b>a>cD.a>b>c5.如图,正方体ABCD﹣A1B1C1D1直线AD1与平面A1C1的夹角为()A.30°B.45°C.90°D.60°6.设f(x)=,x∈R,那么f(x)是()A.奇函数且在(0,+∞)上是增函数B.偶函数且在(0,+∞)上是增函数C.奇函数且在(0,+∞)上是减函数D.偶函数且在(0,+∞)上是减函数7.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于()A.πB.2πC.4πD.8π18.函数在区间上有零点,则实数a的取值范围是()A.a<﹣3B.C.D.9.函数y=的单调递增区间是()A.B.C.D.10.已知定义域为R的偶函数f(x)在[0,+∞)上是增函数,若实数a满足f(log2a)+f(log0.5a)≤2f(1),则a的最小值是()A.B.1C.D.211.设函数表示不超过x的最大整数,则函数y=[f(x)]的值域是()A.{0,1}B.{0,﹣1}C.{﹣1,1}D.{1,1}12.内恒成立,则a的取值范围是()A.B.C.D.二、填空题:本大题共4小题,每小题5分.13.函数的图象恒过定点P,P在幂函数f(x)的图象上,则f(9)=.14.一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为45°,腰和上底均为1(如图),则平面图形的实际面积为.215.函数y=4x﹣2x+1,x∈[﹣3,2]的最大值为.16.设集合A=,B=,函数f(x)=若x0∈A,且f[f(x0)]∈A,则x0的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(10分)(2013秋•赣榆县校级期末)已知全集U=R,函数的定义域为集合A,集合B={x|﹣2<x<a}.(1)求集合∁UA;(2)若A∪B=B,求a的取值范围.18.(12分)(2015春•南昌期中)如图所示,在正方体ABCD﹣A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.19.(12分)(2014秋•嘉峪关校级期末)如图是一个几何体的三视图(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.320.(12分)(2015秋•桃江县校级期中)已知函数.(Ⅰ)当时,利用函数单调性的定义判断并证明f(x)的单调性,并求其值域;(Ⅱ)若对任意x∈[1,+∞),f(x)>0,求实数a的取值范围.21.(12分)(2011•湖北)提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.(精确到1辆/小时).22.(12分)(2013秋•赣榆县校级期末)已知函数(1)求证:函数f(x)在(0,+∞)上为单调增函数;(2)设g(x)=log2f(x),求g(x)的值域;(3)对于(2)中函数g(x),若关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同的实数解,求m的取值范围.42015-2016学年湖南省株洲二中高一(上)12月月考数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U={1,2,3,4,5,6},A={1,2,5},B={2,3,4},则A∩(∁UB)=()A.{2,6}B.{1,5}C.{1,6}D.{5,6}【考点】交、并、...