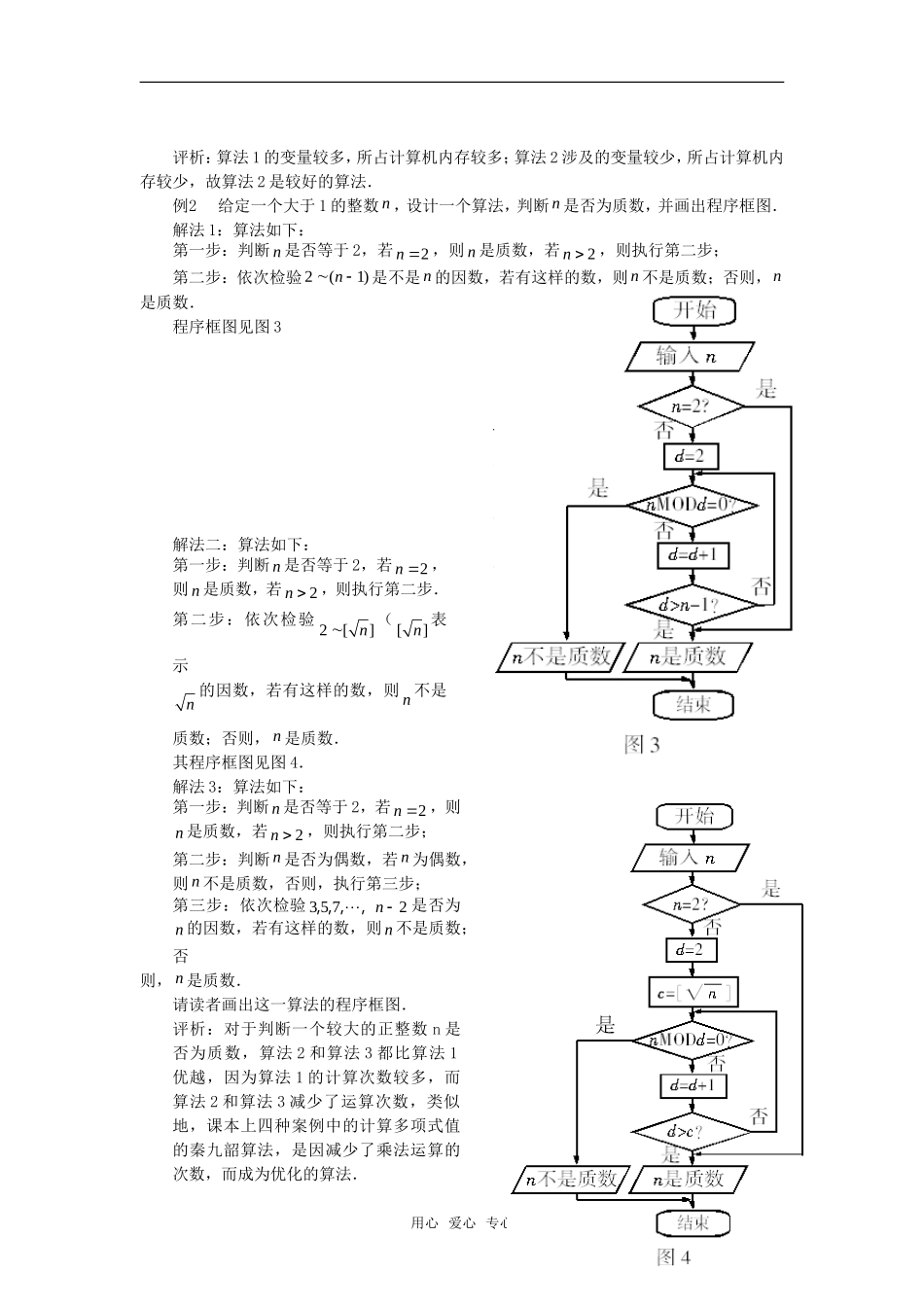
算法优化问题例析我们知道,算法具有不唯一性,但算法具有优劣之分,下面我们通过实例用对比的方法来分析和解决算法的优化问题.例1一位商人有9枚银元,其中1枚略轻的是假银元,你能用天平(无砝码)将假银元找出来吗?写出这一问题的算法.解法1:算法步骤如下:第一步:任取2枚银元分别放在天平的左右两边,如果天平左右不平衡,则轻的那一边就是假银元;如果天平平衡,则进行第二步;第二步:取下右边的银元,放在一边,然后把剩下的7枚银元依次放在右边进行称量,直到天平不平衡,偏轻的那一边就是假银元.解法2:算法(优化的算法)步骤如下:第一步:把9枚银元平均分成3组,每组3枚;法.例2数列即按一定次序排列的一列数.数列中的每一个数都叫做这个数列的“项”,各项依次叫做这个数列的第1项、第2项、…、第n项,一般形式可以写成123naaaa,,,,,其中na是数列的第n项.数列na为斐波那契数列,其中121aa,21nnnaaa.画出程序框图,表示输出此数列的前30项的算法.解法1:程序框图见图1:解法2:程序框图见图2:用心爱心专心评析:算法1的变量较多,所占计算机内存较多;算法2涉及的变量较少,所占计算机内存较少,故算法2是较好的算法.例2给定一个大于1的整数n,设计一个算法,判断n是否为质数,并画出程序框图.解法1:算法如下:第一步:判断n是否等于2,若2n,则n是质数,若2n,则执行第二步;第二步:依次检验2(1)n是不是n的因数,若有这样的数,则n不是质数;否则,n是质数.程序框图见图3解法二:算法如下:第一步:判断n是否等于2,若2n,则n是质数,若2n,则执行第二步.第二步:依次检验2[]n([]n表示n的因数,若有这样的数,则n不是质数;否则,n是质数.其程序框图见图4.解法3:算法如下:第一步:判断n是否等于2,若2n,则n是质数,若2n,则执行第二步;第二步:判断n是否为偶数,若n为偶数,则n不是质数,否则,执行第三步;第三步:依次检验3572n,,,,是否为n的因数,若有这样的数,则n不是质数;否则,n是质数.请读者画出这一算法的程序框图.评析:对于判断一个较大的正整数n是否为质数,算法2和算法3都比算法1优越,因为算法1的计算次数较多,而算法2和算法3减少了运算次数,类似地,课本上四种案例中的计算多项式值的秦九韶算法,是因减少了乘法运算的次数,而成为优化的算法.用心爱心专心规律总结:优化的算法具有以下显著的特点:1.能使运算难度降低或运算次数减少;2.使计算机便于运行,提高运算速度;3.能使所占计算机内存减少用心爱心专心