高考数学一轮复习 第8章 立体几何 第10课时练习 理-人教版高三全册数学试题VIP免费

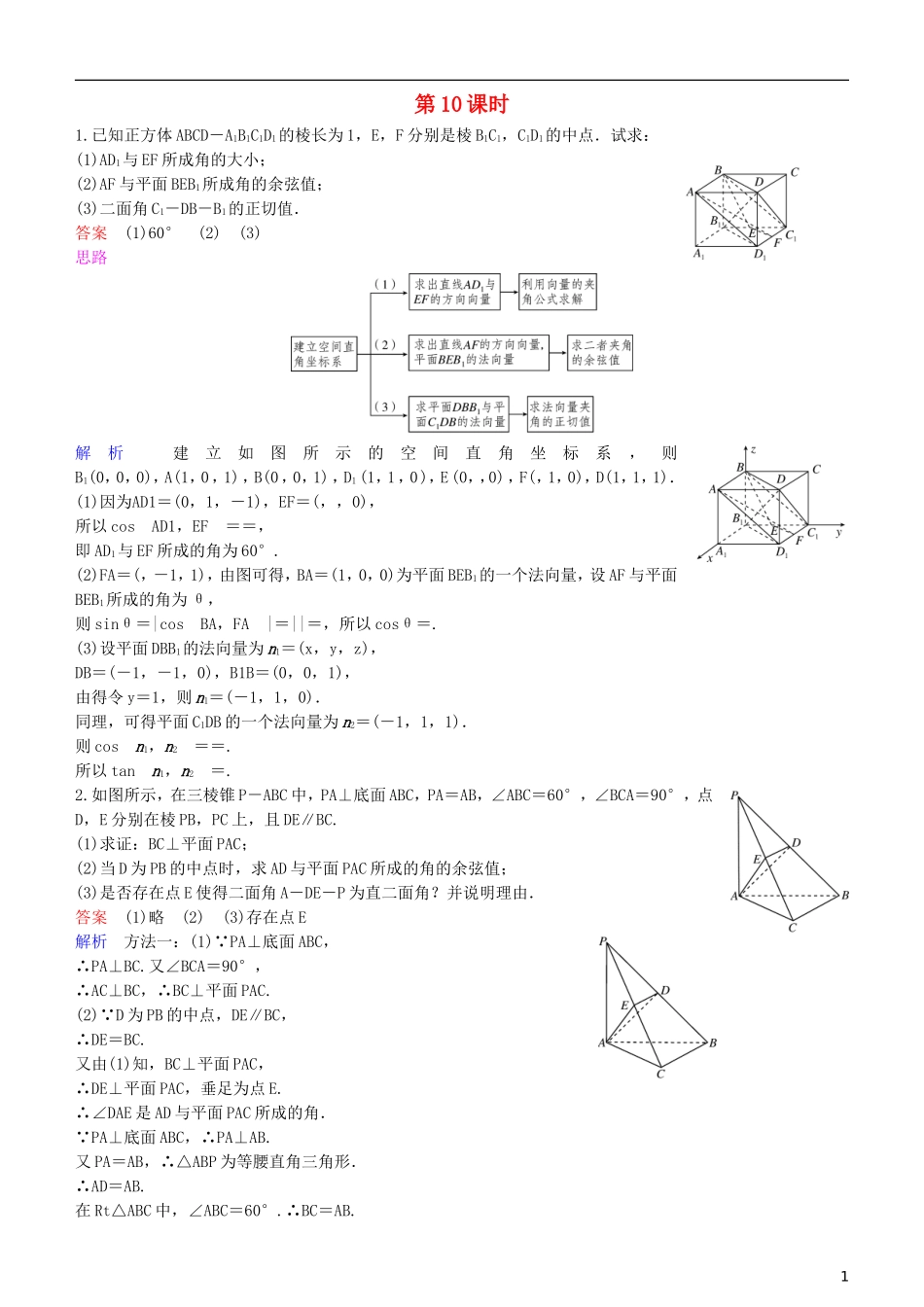
第10课时1.已知正方体ABCD－A1B1C1D1的棱长为1，E，F分别是棱B1C1，C1D1的中点．试求：(1)AD1与EF所成角的大小；(2)AF与平面BEB1所成角的余弦值；(3)二面角C1－DB－B1的正切值．答案(1)60°(2)(3)思路解析建立如图所示的空间直角坐标系，则B1(0，0，0)，A(1，0，1)，B(0，0，1)，D1(1，1，0)，E(0，，0)，F(，1，0)，D(1，1，1)．(1)因为AD1＝(0，1，－1)，EF＝(，，0)，所以cosAD1，EF＝＝，即AD1与EF所成的角为60°.(2)FA＝(，－1，1)，由图可得，BA＝(1，0，0)为平面BEB1的一个法向量，设AF与平面BEB1所成的角为θ，则sinθ＝|cosBA，FA|＝||＝，所以cosθ＝.(3)设平面DBB1的法向量为n1＝(x，y，z)，DB＝(－1，－1，0)，B1B＝(0，0，1)，由得令y＝1，则n1＝(－1，1，0)．同理，可得平面C1DB的一个法向量为n2＝(－1，1，1)．则cosn1，n2＝＝.所以tann1，n2＝.2.如图所示，在三棱锥P－ABC中，PA⊥底面ABC，PA＝AB，∠ABC＝60°，∠BCA＝90°，点D，E分别在棱PB，PC上，且DE∥BC.(1)求证：BC⊥平面PAC；(2)当D为PB的中点时，求AD与平面PAC所成的角的余弦值；(3)是否存在点E使得二面角A－DE－P为直二面角？并说明理由．答案(1)略(2)(3)存在点E解析方法一：(1) PA⊥底面ABC，∴PA⊥BC.又∠BCA＝90°，∴AC⊥BC，∴BC⊥平面PAC.(2) D为PB的中点，DE∥BC，∴DE＝BC.又由(1)知，BC⊥平面PAC，∴DE⊥平面PAC，垂足为点E.∴∠DAE是AD与平面PAC所成的角． PA⊥底面ABC，∴PA⊥AB.又PA＝AB，∴△ABP为等腰直角三角形．∴AD＝AB.在Rt△ABC中，∠ABC＝60°.∴BC＝AB.1∴Rt△ADE中，sin∠DAE＝＝＝.∴cos∠DAE＝.(3) DE∥BC，又由(1)知，BC⊥平面PAC，∴DE⊥平面PAC.又 AE⊂平面PAC，PE⊂平面PAC，∴DE⊥AE，DE⊥PE.∴∠AEP为二面角A－DE－P的平面角． PA⊥底面ABC，∴PA⊥AC，∴∠PAC＝90°.∴在棱PC上存在一点E，使得AE⊥PC.这时，∠AEP＝90°.故存在点E使得二面角A－DE－P是直二面角．方法二：如图所示，以A为原点建立空间直角坐标系A－xyz.设PA＝a，由已知可得A(0，0，0)，B(－a，a，0)，C(0，a，0)，P(0，0，a)．(1) AP＝(0，0，a)，BC＝(a，0，0)，∴BC·AP＝0，∴BC⊥AP.又 ∠BCA＝90°，∴BC⊥AC.又AP∩AC＝A，∴BC⊥平面PAC.(2) D为PB的中点，DE∥BC，∴E为PC的中点．∴D(－a，a，a)，E(0，a，a)．又由(1)知，BC⊥平面PAC，∴DE⊥平面PAC，垂足为点E.∴∠DAE是AD与平面PAC所成的角． AD＝(－a，a，a)，AE＝(0，a，a)，∴cos∠DAE＝＝.(3)同方法一．3．(2018·辽宁沈阳一模)如图，在三棱柱ABC－A1B1C1中，侧面AA1C1C⊥底面ABC，AA1＝A1C＝AC＝AB＝BC＝2，且O为AC的中点．(1)求证：A1O⊥平面ABC；(2)求二面角A－A1B－C1的余弦值．答案(1)略(2)－解析(1) AA1＝A1C，且O为AC的中点，∴A1O⊥AC，又侧面AA1C1C⊥底面ABC，交线为AC，且A1O⊂平面AA1C1C，∴A1O⊥平面ABC.(2)如图，连接OB，以O为坐标原点，OB，OC，OA1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系．2由已知可得A(0，－1，0)，A1(0，0，)，C1(0，2，)，B(，0，0)，∴AB＝(，1，0)，A1B＝(，0，－)，A1C1＝(0，2，0)．设平面AA1B的法向量为m＝(x1，y1，z1)．则有⇒取x1＝1，则y1＝－，z1＝1，∴m＝(1，－，1)，为平面AA1B的一个法向量．设平面A1BC1的法向量为n＝(x2，y2，z2)，则有⇒y2＝0，令x2＝1，则z2＝1，∴n＝(1，0，1)，为平面A1BC1的一个法向量，∴cos〈m，n〉＝＝＝.易知二面角A－A1B－C1的平面角为钝角，∴所求二面角的余弦值为－.4．(2018·河北开滦二中月考)如图所示，在四棱锥P－ABCD中，PD⊥平面ABCD，底面ABCD是正方形，PD＝AB＝2，E为PC中点．(1)求证：DE⊥平面PCB；(2)求点C到平面DEB的距离；(3)求二面角E－BD－P的余弦值．答案(1)略(2)(3)解析(1)证明： PD⊥平面ABCD，∴PD⊥BC.又正方形ABCD中，CD⊥BC，PD∩CD＝D，∴BC⊥平面PCD. DE⊂平面PCD，∴BC⊥DE. PD＝CD，E是PC的中点，∴DE⊥PC.又 PC∩BC＝C，∴DE⊥平面PCB.(2)如图①所示，过点C作CM⊥BE于点M，由(1)知平面DEB⊥平面PCB， 平面DEB∩平面PCB＝BE，∴CM⊥平面DEB.∴线段CM的长度就是点C到平面DEB的距离． PD＝...