广西桂林市高一数学上学期期末试卷（含解析）-人教版高一全册数学试题VIP免费

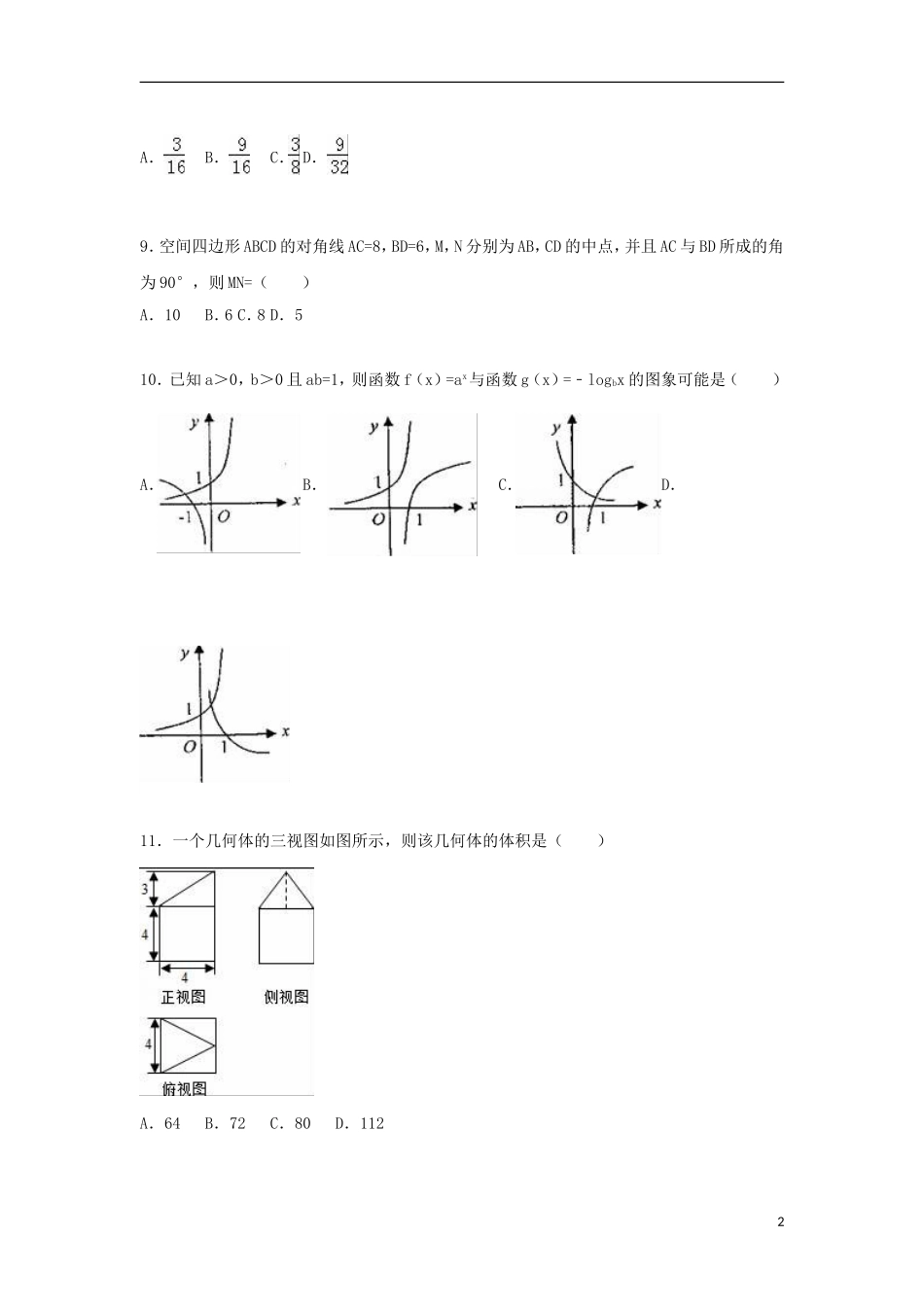
2015-2016学年广西桂林市高一（上）期末数学试卷一、选择题（12*5=60’）1．已知全集U={1，2，3，4，5，6}，集合A={1，2，5}，∁UB={4，5，6}，则集合A∩B=（）A．{1，2}B．{5}C．{1，2，3}D．{3，4，6}2．已知平面上两点A（﹣1，1），B（5，9），则|AB|=（）A．10B．20C．30D．403．下列函数中，在（0，+∞）上为减函数的是（）A．f（x）=3xB．C．D．4．设f（x）=，则f（f（﹣2））=（）A．﹣1B．C．D．5．若幂函数f（x）=（m2﹣m﹣1）xm在（0，+∞）上为增函数，则实数m=（）A．2B．﹣1C．3D．﹣1或26．已知直线l1：x+2ay﹣1=0，与l2：（2a﹣1）x﹣ay﹣1=0平行，则a的值是（）A．0或1B．1或C．0或D．7．若定义在R上的偶函数f（x）在[0，+∞）上是减函数，则有（）A．f（3）＜f（﹣2）＜f（1）B．f（1）＜f（﹣2）＜f（3）C．f（﹣2）＜f（1）＜f（3）D．f（3）＜f（1）＜f（﹣2）8．过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为（）1A．B．C．D．9．空间四边形ABCD的对角线AC=8，BD=6，M，N分别为AB，CD的中点，并且AC与BD所成的角为90°，则MN=（）A．10B．6C．8D．510．已知a＞0，b＞0且ab=1，则函数f（x）=ax与函数g（x）=﹣logbx的图象可能是（）A．B．C．D．11．一个几何体的三视图如图所示，则该几何体的体积是（）A．64B．72C．80D．112212．已知函数f（x）=log2（a2x﹣4ax+1），且0＜a＜1，则使f（x）＞0成立的x的取值范围是（）A．（﹣∞，0）B．（0，+∞）C．（﹣∞，2loga2）D．（2loga2，+∞）二、填空题（4*5=20’）.13．计算：=．14．直线3x+4y﹣5=0到直线3x+4y+15=0的距离是．15．在边长为a的等边三角形ABC中，AD⊥BC于D，沿AD折成二面角B﹣AD﹣C后，，这时二面角B﹣AD﹣C的大小为．16．如图，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，且AF==a，G是EF的中点，则GB与平面AGC所成角的正弦值为．三、解答题（共6题，70分，解答应给出文字说明，证明过程及演算步骤.）317．求下列函数的定义域：（1）f（x）=log2（2）f（x）=．18．在平面直角坐标系xoy中，已知△ABC的顶点坐标为A（2，4），B（1，﹣2），C（﹣2，3）．（1）求直线BC的方程；（2）求边BC上高AD所在的直线方程．19．已知函数f（x）=（1）在下表中画出该函数的草图；（2）求函数y=f（x）的值域、单调增区间及零点．20．某投资公司计划投资A、B两种金融产品，根据市场调查与预测，A产品的利润y与投资量x成正比例，其关系如图1，B产品的利润y与投资量x的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）（1）分别将A、B两产品的利润表示为投资量的函数关系式；（2）该公司已有10万元资金，并全部投入A、B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？421．如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，点D是AB的中点．求证：（1）AC⊥BC1；（2）AC1∥平面B1CD．22．已知定义域为R的函数f（x）=（a，b是常数）是奇函数．（1）求函数f（x）的解析式；（2）判断函数f（x）的单调性，并证明你的结论；（3）若对于任意都有f（kx2）+f（2x﹣1）＞0成立，求实数k的取值范围．52015-2016学年广西桂林市高一（上）期末数学试卷参考答案与试题解析一、选择题（12*5=60’）1．已知全集U={1，2，3，4，5，6}，集合A={1，2，5}，∁UB={4，5，6}，则集合A∩B=（）A．{1，2}B．{5}C．{1，2，3}D．{3，4，6}【考点】交集及其运算．【专题】集合．【分析】由题意全集U={1，2，3，4，5，6}，CUB={4，5，6}，可以求出集合B，然后根据交集的定义和运算法则进行计算．【解答】解： 全集U={1，2，3，4，5，6}，又 ∁UB={4，5，6}，∴B={1，2，3}， A={1，2，5}，∴A∩B={1，2}，故选：A．【点评】此题主要考查集合和交集的定义及其运算法则，是一道比较基础的题．2．已知平面上两点A（﹣1，1），B（5，9），则|AB|=（）A．10B．20C．30D．40【考点】两点间距离公式的应用．【专题】计算题；转化思想；综合法；直线与圆．【分析】利用两点间距离公式求解．【解答】解： 平面上两点A（﹣1，1），B（5，9），∴|...